微分方程模型概念解析

微分方程模型按照所含未知函数的类型分为常微分方程模型（未知函数为一元函数）和偏微分方程模型（未知函数为多元函数），模型建立的一般步骤为：

（1）翻译和转化；

（2）建立瞬时表达式；

（3）配备物理单位；

（4）确定初始条件等。

常用的建立微分方程模型的方法有：

1.定理、定率法：根据已知基本定律或者基本公式建立的微分方程模型，经常用于涉及到数学、力学、电学、化学等领域中定理、定律的问题。

【示例1.1.1】——牛顿第二定律

假设质量为m的物体在空中下降，空气阻力与物体的速度平方成正比，比例系数为k，求物体的运动规律。

解　设物体的下落距离为x，则物体的下落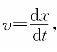速度为，加速度为

根据牛顿第二定律F＝ma，建立微分方程模型为：

2.定义法：利用导数定义建立的微分方程模型，经常用于涉及到变化率、放射率等考古学、化学、经济学领域中的问题。

【示例1.1.2】——古尸年代鉴定

在某个古墓的洞穴中，发现了某古代人类的人骨碎片，科学家们对人骨碎片进行碳14鉴定，分析c14与c 12的比例仅仅是活动组织内的6.24%，试判断此类人生活在多少年前？（提示：活体中放射性同位素c 14的数量与稳定元素c 12的数量成定比，生物体死后，放射性c14便以每年八千分之一的速度减少）(www.xing528.com)

解　设t为死亡年数，y为第t年后生物体内的c 14数量，则建立微分方程模型为：

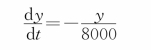
3.微元法：利用微元思想建立的微分方程模型，经常用于几何学中面积、体积的计算，物理学中变力做功及河流中污染物分析等相似问题的求解。

【示 例1.1.3】容　器 放 水 时 间 如 图1.1.1所示，一个半径为R的半球形容器内开始时盛满了水，但由于其底部一个面积为S cm2的小孔在t＝0时刻被打开，水被不断放出，试问容器内的水被放完总共需要多少时间？

解　记r为t时刻的水面半径，h（t）为t时刻容器中水的高度，v（t）为水从小孔流出的速度，且r2＝R 2－（R－h）2。

设在微小时间间隔［t，t＋d t］内，水面高度由h降至h＋d h（d h＜0），由此可得：

据此建立微分方程模型为：

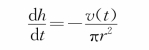
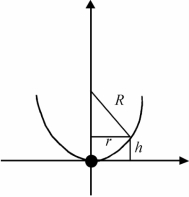
图1.1.1　容器示意图

其中，（假设忽略内部摩擦力和表面张力）。

4.模拟近似法：许多现实问题中内部规律比较模糊，很难得到确定的数学关系，因而需要在不同的假设条件下模拟现实问题，得到近似的函数关系建立微分方程模型，如交通指示灯中黄灯时间的设定等。