矩阵在现实生活中的应用

矩阵本质上就是一个数表，而这个数表可以通过矩阵的运算进行变换得到新的数表。如果了解原始数表的含义，而且可以从中抽象出某种变化规律，那么就可以对数表进行变换，得到想要的结论。在日常生活中，矩阵在各个领域都有广泛的应用，例如，生产成本问题、人口流动问题、密码学以及超市物品配送等都和矩阵息息相关。下面，通过几个具体的实例来了解一下矩阵在实际生活中的应用。

【示例4.3.1】——生产成本问题

某厂家生产三种产品，在最近一个月内共生产三批产品，每批产品的总成本以及每种产品产量均可控制，具体情况如表4.3.1所示，试计算三种产品单位成本各为多少？

表4.3.1　产品产量表

解　设三种产品每个批次的单位成本分别为x 1、x 2、x 3，由此建立方程组为：

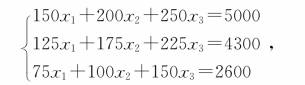
则系数矩阵，常数项矩阵变量矩阵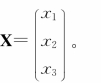

（1）逆矩阵法求解

命令窗口编写MATLAB代码如下：

运行后得到输出结果为：

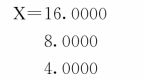
根据上述结果可知，产品A、B、C的单位成本分别为16.0元、8.0元、4.0元。

（2）高斯消元法求解

命令窗口编写MATLAB代码如下：

运行后得到输出结果为：

根据上述结果可知，r1＝r2＝3，所以方程组有解，且有唯一解。利用行最简形矩阵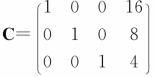，可将线性方程组AX＝B转换为：

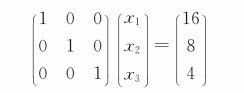
因而可得线性方程组的唯一解为：x 1＝16，x 2＝8，x 3＝4，故产品A、B、C的单位成本分别为16.0元、8.0元、4.0元。

【示例4.3.2】——行业人口流动问题

假设某个中小城市及郊区乡镇共有40万人从事农、工、商工作，假定总人数在若干年内保持不变，社会调查表明：

（1）目前约有25万人从事农业，10万人从事工业，5万人经商；

（2）在务农人员中，每年约有10%改为务工，10%改为经商；

（3）在务工人员中，每年约有10%改为务农，20%改为经商；

（4）在经商人员中，每年约有10%改为务农，20%改为务工。

请预测一年、二年及十年后从事各行业人员的人数及其发展趋势。

解　假设x i，y i，zi分别表示第i年后从事这三种职业的人员总数，且已知x 0＝25，y 0＝10，z 0＝5。依据题意，有

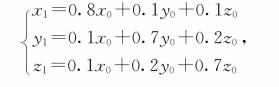
即

则

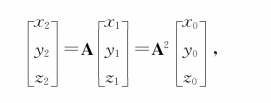
依次类推

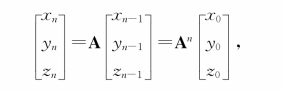
其中，一、二、十年后从事各行业的人数可以通过MATLAB软件计算。

命令窗口编写MATLAB代码如下：

运行后得到输出结果为：

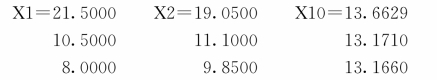
根据上述结果可知，一年后务农人员有21.5万，务工人员10.5万，经商人员8万；两年后务农人员19.05万，务工人员11.1万，经商人员9.85万；十年后务农人员13.6629万，务工人员13.1710万，经商人员13.1661万。

编写M-函数文件，命名为people.m，分别计算1，2，3，4，5，…，100年后各行业的人数，绘制各行业人数的变化趋势。(www.xing528.com)

命令窗口输入MATLAB代码如下：

运行后得到输出结果如图4.3.1所示。

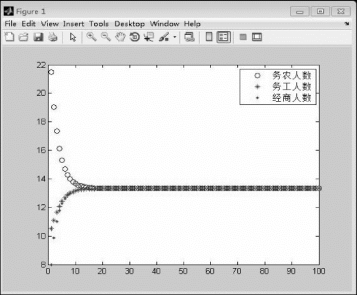
图4.3.1　各行业人数变化曲线图

根据图4.3.1可以看出，务农人数在逐年减少，务工和经商的人数在逐年增加，最后三个行业的人数趋于相等。

【示例4.3.3】——密码问题

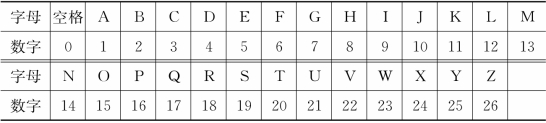
按照表4.3.2中对应关系，将26个字母与整数1～26进行一一对应，英文状态下的空格对应数字0，设加密矩阵利用矩阵乘法对信息“It is good”进行加密和解密。（注　加密矩阵的行列式必须为±1）

表4.3.2字母与数字对应关系表

解　【加密过程】

首先按照表4.3.2中所示的数字字母对应关系表将英文信息转换为矩阵A，因为加密矩阵为3阶方阵，故转换的矩阵A为3行的矩阵，将英文字母转换后按列排放，则信息矩阵为：

注　信息“It is good”加上中间的空格共有10个字符，而生成的矩阵A为3行4列的矩阵，最后一列空出的元素用0补齐。然后对信息矩阵A左乘加密矩阵X得到新的加密后矩阵，记为密码矩阵B，即B＝XA。

命令窗口输入MATLAB代码如下：

运行后得到输出结果为：

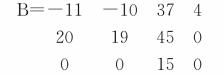
根据上述结果可知，密码矩阵B中有的元素大于26，这就无法对应到字母中去，这样就给解密过程带来了困难，因而需要进一步进行加密处理。

第二次加密过程需要对密码矩阵B进行取模运算，也就是用矩阵B中的元素除以27后的余数按列排列得到新的加密矩阵C。

命令窗口输入MATALB代码，计算二次加密矩阵C如下：

运行后得到输出结果为：

将结果中的二次加密矩阵C利用表4.3.2中的关系对应后得到英文信息为：

如果用户不知道该条消息经过加密处理，或者不知道加密矩阵是什么，就会完全不理解这条信息的含义。

【解密过程】

结果中的矩阵C就是最终的加密矩阵，将此矩阵发送给其他用户后，再通过相应的解密过程，即可得到原来的信息矩阵A，再利用数字、字母关系对应表对应出相应的英文消息，具体的解密过程为：

对二次加密矩阵C左乘解密矩阵X－1，再利用取模运算即可得到最初的信息矩阵A，命令窗口输入MATLAB代码如下：

运行后得到输出结果为：

将信息矩阵A按照表4.3.2进行对应，得到的英文消息为：

这条消息与最初发送者发的消息相同，因此解密成功。

【能力训练4.3】

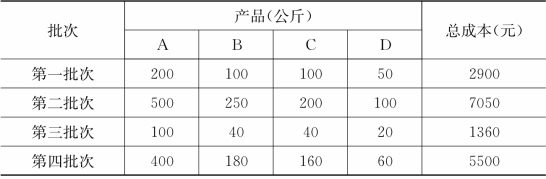
1.某工厂在一次投料生产中能获得四种产品，每次投料的总成本

表1　成本表

2.假设某中小城市及郊区乡镇的人口总数为100万，人口总数每年以千分之4.79的比例增长。目前，该城市的城镇人口有38万，农村人口有62万，每年农村人口按照千分之1的比例流向城镇，请计算5年、10年后的城镇、农村人口分别是多少，并预测未来该城市城镇、农村人口的变化趋势。

3.按照表4.3.1中对应关系，将26个字母与整数1～26进行一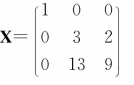一对应，英文状态下的空格对应数字0，利用加密矩阵见表1，试建立M文件计算每种产品的单位成本。对信息“It is beautiful”进行加密，并解密验证。