对于线性方程组AX＝B，若系数矩阵A不是方阵或者A不可逆，则利用逆矩阵法无法计算出方程组的解。在这种情况下，可以用高斯消元法（即初等行变换）将线性方程组化为阶梯型方程组，该阶梯型方程组与原方程组同解。
在MATLAB软件中，求解线性方程组的解之前判断方程组有无解（若r（A）＝r（［A，B］），则方程组有解；否则无解），然后利用将矩阵A化为行最简形（阶梯形矩阵），最后得到线性方程组的解。
【示例4.2.2】求解线性方程组
解 首先将上述线性方程组用矩阵形式表示为：AX＝B。
其中，
将增广矩阵A｜B化为行最简形，记为C，则有
从而可以得到线性方程组的解。
命令窗口编写MATLAB代码如下：
运行后得到输出结果为：
根据上述结果可知，rank（A）＝rank（［A，B］）＝3，所以该方程有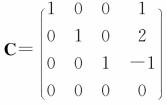
，可将线性方程组AX＝B转换为：
解，且有唯一解。利用行最简形矩阵
因而可得线性方程组的唯一解为x 1＝1，x 2＝2，x 3＝－1。
【示例4.2.3】求解方程组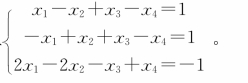
解 首先将上述线性方程组用矩阵形式表示为：AX＝B。
其中，
将增广矩阵A｜B化为行最简形，记为C，则有
从而可以得到线性方程组的解。
命令窗口编写MATLAB代码如下：
运行后得到输出结果为：
根据上述结果可知，r1＝r2＝2，但由rank（A）＝rank（［A，B］）＝2＜4（未知数的个数）可知，该方程组有无数多组解。(www.xing528.com)
根据行最简形矩阵
，可将线性方程组AX＝B转换为：
原方程组对应的阶梯型方程组为：
则方程组的解为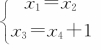
（x 2，x 4是自由变量）。
【示例4.2.4】求解方程组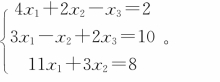
解 首先将上述线性方程组用矩阵形式表示为：AX＝B。
其中，
将增广矩阵A｜B化为行最简形，记为C，则有
从而可以得到线性方程组的解。
命令窗口编写MATLAB代码如下：
运行后得到输出结果为：
根据上述结果可知，rank（A）≠rank（［A，B］），所以该方程组无解。
【能力训练4.2】
1.填空题：
（1）MATLAB软件中利用逆运算计算线性方程组AX＝B的解的命令为________；
（2）MATLAB 软件中将矩阵转化为行最简形矩阵的命令代码为________；
（3）判断线性方程组是否有解的条件为________；
（4）MATLAB软件中生成列向量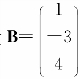
的命令代码为______；
（5）提取行最简形矩阵C的前4列所有元素的命令代码为______。
2.编写代码求解下列线性方程组：
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
