微分运算和曲线绘制：函数y=x^3+2x^2-1的导数和图像

diff——计算一元函数或多元函数微分

【语法】

y＝diff（f，x）返回符号表达式f关于x的一阶导数或一阶偏导数y；

y＝diff（f，x，n）返回符号表达式f关于x的n阶导数。

注　上述调用格式中的参数x可以缺省，缺省时系统根据符号表达式自动确定自变量。

【示例3.2.3】根据导函数的定义，计算函数y＝x 3＋2x 2－1在x＝1处的导数值，并绘制函数曲线图和切线图。

解　根据高等数学的知识可知，函数在点x 0处的导数定义为一个极限表达式，即：，为方便书写，在命令窗口中用a代替Δx。

（1）计算点x 0处切线的斜率，确定切线方程

命令窗口编写MATLAB代码如下：

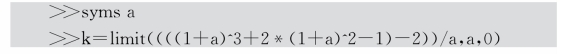
运行后得到输出结果为：

根据上述结果可知，函数y＝x 3＋2x 2－1在（1，2）点处的切线斜率为7，则该函数在x＝1处的切线方程为y＝7x－5。

（2）绘制函数曲线图和x＝1处的切线图

命令窗口编写MATLAB代码如下：

运行后得到输出结果如图3.2.2所示。

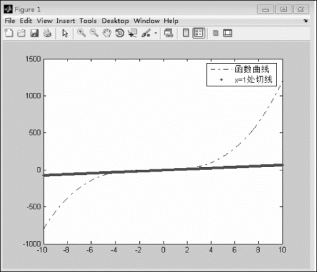
图3.2.2　函数y＝x 3＋2x 2－1及其切线图

【示例3.2.4】利用diff（）命令，计算函数y＝sin x的导函数，并绘制函数曲线、导函数曲线和直线y＝0的图像，观察函数单调性和导函数之间的关系。(www.xing528.com)

解　（1）计算函数y＝sin x的导函数命令窗口编写MATLAB代码如下：

运行后得到输出结果为：

根据上述结果可知，函数y＝sin x的导函数为y′＝cos x。

（2）绘制函数曲线、导函数曲线和直线y＝0的图像

建立M-命令文件，编辑窗口输入MATLAB代码如下：

保存M-命令文件，命名为dsin.m，在命令窗口输入dsin，运行后得到输出结果如图3.2.3所示。

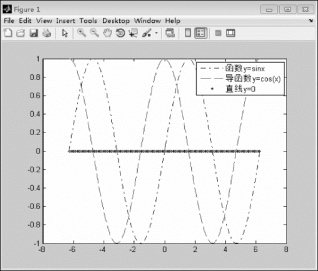
图3.2.3　函数y＝sin x及其导函数图

通过观察图3.2.3可知，当函数y＝sin x呈上升趋势（单调递增）时，导函数y＝cos x的函数曲线在直线y＝0的上方（即导函数值大于0）；当函数y＝sin x呈下降趋势（单调递减）时，导函数y＝cos x的函数曲线在直线y＝0的下方（即导函数值小于0）；当函数y＝sin x取得极值±1时，导函数y＝cos x的曲线恰好与直线y＝0相交（即导函数值为0）。

【示例3.2.5】利用diff（）命令，分别计算函数z＝e2x＋y关于变量x的一阶和二阶导函数，及关于变量y的一阶导函数。

命令窗口编写MATLAB代码如下：

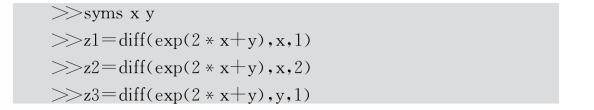
运行后得到输出结果为：

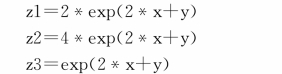
根据上述结果可知，函数z＝e2x＋y关于变量x的一阶导数为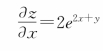，关于x的二阶导数为，关于y的一阶导数为