物联网与传感器技术中的点定位方法

1.节点定位

节点定位是无线传感器网络的重要技术，位置信息是确认感知到的信息状态是处于具体空间，是监测事件在网络区域中的位置。确认获得的区域信息，并可通过相连信息估计出全局的状态。如在战场环境中，通过单兵携带传感器节点观察周边的状态，为指挥系统提供对全局判断的依据。尤其在复杂环境（如巷战）中，可为邻近友军不仅能提供清晰的图像，还能提供准确的位置。这对战场来说，无论是准确打击，还是也加搜救，都提供了强大的技术支持。在实际应用中，大规模节点往往通过飞机或高射炮随机抛撒，节点的位置和相互关系不具有预知性。

基于位置的路由协议、分簇和数据聚集算法、拓扑控制、覆盖控制等协议都需要知道节点的位置信息，可为用户提供很多的定位服务。因此，在网络自组织过程中，需借助定位算法或安装辅助定位设备，如GPS对节点进行定位，以充分发挥网络功能。随着无线传感器网络向节点数量多、铺设范围广、基础设施简单和硬件成本低的方向发展，如何在减少节点硬件组件、算法实现简单的同时，获得相对准确的定位信息已成为主要研究的课题之一。

定位算法通常分为两类：绝对定位算法和相对定位算法，通过是否需要知道自己的位置（锚节点）或信标节点来区分其性质。在待测区域事先布置一定比例锚节点的，称为绝对定位算法。这些节点通过GPS或其他方法来获得自身绝对坐标，其余的未知节点通过与这些信标节点通信获得自身坐标。相对定位算法无需事先布置信标节点，通过算法制定方案，选取一定数量的未知节点建立相对坐标，其余的节点通过节点之间的协作关系和消息传输获取自身在相对坐标系中的相对位置实现定位。相对定位算法无需锚节点和基础设施，硬件成本低，并且不会受复杂环境对远距离信号传输的影响，适合于对节点硬件、能耗以及环境适应性有很高要求的无线传感器网络应用。节点定位算法的评价指标如下：

1）定位准确度。定位技术首要的评价指标是定位准确度，一般用误差值与节点通信半径之比表示。不同类型的定位算法准确度差异较大。基于距离的定位方法有较高的定位准确度，但节点体积、功耗和成本也大。

2）锚节点密度。锚节点是位置已知的节点，通常采用人工固定布置或用GPS获得准确位置。人工部署的方式不仅受网络部署环境的限制，还严重制约了网络的可扩展性；采用GPS确定锚节点位置，节点体积和代价增大。因此，锚节点密度也是评价定位算法性能的重要指标之一。

3）鲁棒性和容错性。通常定位系统和算法都需要比较理想的无线通信环境和可靠的网络节点设备。但在真实应用场合中，常会有诸如以下的问题。外界影响和节点硬件准确度限制造成节点间点到点的距离或角度测量误差增大的问题；外界环境中存在严重的多径传播、衰减、阴影、非视距（NLOS）、通信盲点等问题；网络节点由于周围环境或自身原因（如电池耗尽、物理损伤）而出现失效的问题。由于环境、能耗和其他原因，人工维护或替换传感器节点或使用其他高准确度的测量手段常常是十分困难或不可行的。因此，定位系统和算法的软、硬件必须具有很强的容错性和自适应性，能够通过自动调整或重构纠正错误、适应环境、减小各种误差的影响，以提高定位准确度。

4）能耗。能耗是对传感器网络的设计和实现影响最大的因素之一。由于传感器节点电池能量有限，因此在保证定位准确度的前提下，与功耗密切相关的定位所需的计算量、通信开销、存储开销、时间复杂性、系统的附加设备能量消耗是一组关键性指标。

2.基于距离的定位算法

根据定位机制可将现有无线传感器网络自身定位算法分为基于距离的和非基于距离的定位算法两类。基于距离的定位算法通过测量相邻节点之间的绝对距离或方位，并利用节点之间的实际距离来计算未知节点的位置；非基于距离的定位算法则无需距离和角度信息，仅根据网络连通性等信息实现定位。

基于距离的节点定位一般包括3个部分，即距离测定、位置计算和定位过程。

（1）距离测定

基于测距的算法通过节点自身携带的测距功能直接测量两个节点之间的距离，比较重要的测距方法主要有到达时间、到达时间差和信号强度测距或者到达角测距。

1）到达时间（TOA）：该技术通过测量信号传播时间来测量距离。使用TOA技术最基本的定位系统是GPS，GPS需要昂贵、高性能的电子设备来准确同步卫星时钟。因节点硬件尺寸、价格和功耗限制，GPS和其他TOA技术无法广泛应用于无线传感器网络。测距技术被广泛应用于节点定位方案中。通过记录两种不同信号（常使用RF和超声波）到达时间差，基于已知信号传播速度，把时间转化为距离。已有使用多种定位算法实现测距，但该技术受限于超声波传播距离有限（超声波信号通常传播距离仅为20～30ft（1ft=0.3048m），因而网络需要密集部署）和NLOS问题对超声波信号的传播影响。虽然已有发现并减轻NLOS影响的技术，但都需要大量计算和通信开销，不适用于低功耗的无线传感器网络。

2）接收信号强度指示（RSSI）：已知发射功率，在接收节点测量接收功率，计算传播损耗，使用理论或是经验的信号传播模型将传播损耗转化为距离，该技术主要使用RF信号。因传感器节点具有无线通信能力，故RSSI是一种低功率、廉价的测距方式。其主要误差来源是环境影响所造成的信号传播模型的建模复杂性、反射、多径传播、NLOS以及天线增益等问题，这些都会对相同的距离产生显著不同的传播损耗。通常将其看作一种粗糙的测距技术，它可能产生50%的测距误差。

3）到达角（AoA）：该技术是估算邻节点发送信号方向，可通过天线阵列或多个接收器来实现，除定位外，还能提供方向信息。

（2）位置计算

在获取上述距离值之后，节点需要通过位置计算的方法计算得到坐标值。现有的算法一般采用三边测量法、三角测量法和极大似然法计算坐标。

三边测量法对未知节点获得3个以上的信标节点距离值之后，就可通过式（5-18）计算自身坐标。

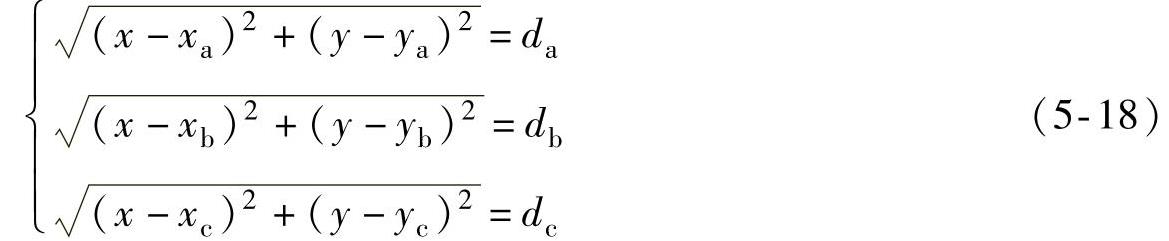
式中，（x_a，y_a）、（x_b，y_b）、（x_c，y_c）分别是3个信标节点的坐标；d_a、d_b、d_c是未知节点到3个信标节点的距离。

经过线性化，可得线性方程式

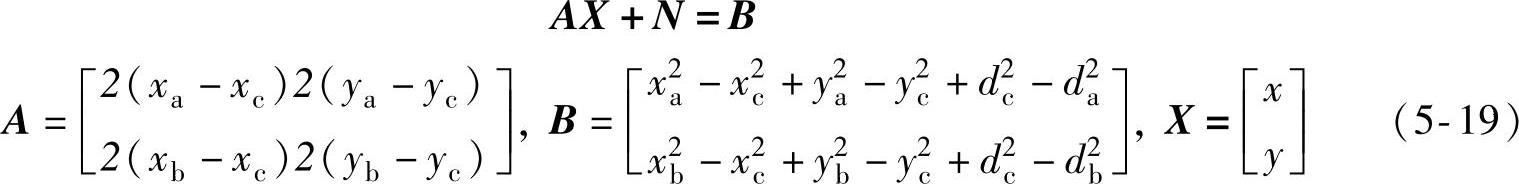
使用标准的最小均方差估计可得未知节点的坐标为

X=（AA^T）^-1A^Tb （5-20）

式（5-19）中的N是由于存在测距误差引入的参数，它是根据测距误差的分布形式存在的一个随机误差矢量。如果未知节点测得的到信标节点的距离值大于3个，则可以加入式（5-20）中，进行更准确的计算。

三角测量定位方法也称为AoA定位方法或方位测量定位方法，该方法通过未知节点接收器天线或天线阵列测出锚节点发射电波的入射角，从而构成从目标节点到锚节点的径向线，即方位线。在二维平面中，利用两个或更多锚节点的AoA测量值，按照AoA定位算法确定多条方位线的交点，即可计算出未知节点的估计位置。

假设未知节点A的坐标为（x₀，y₀），分别测得锚节点B、锚节点C的信号到达角为θ₁和θ₂，则

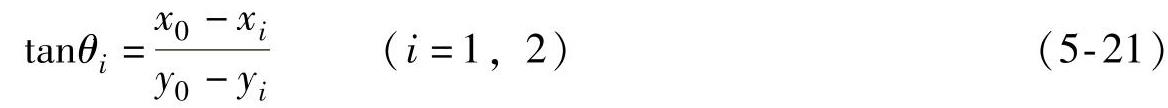
三边测量法和三角测量法由于涉及大量的矩阵运算和最小二乘的运算，计算量较大。针对这种情况，加州大学洛杉矶分校在定位算法中提出的最大最小值法通过简单的折线运算估计未知节点的位置，如图5-14所示。图中A点和B点为信标节点，C点为未知节点。在获得C点到A点和B点的折线距离a、b、c之后，在三角形ACK中，利用斜边AC的长度a代替直角边AK的长度，从而K点移动到K′点，B点类似。使用标准的最小均方差估计法，可得节点D的坐标为

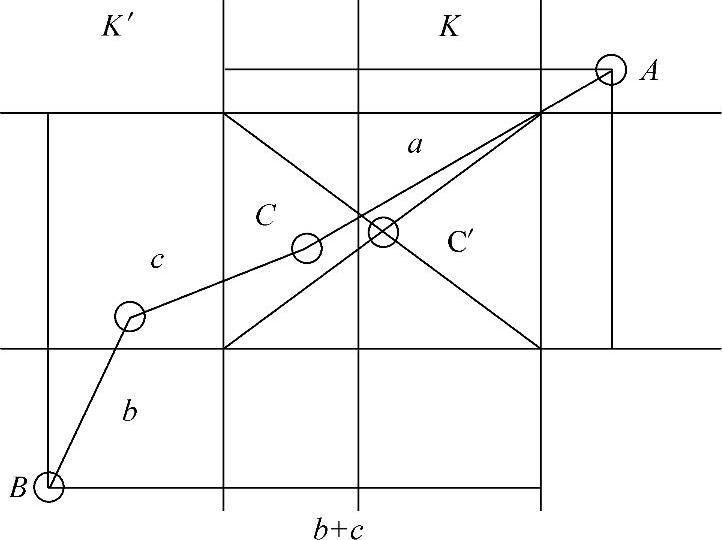
图5-14 最大最小值法示意图

（3）定位过程

不同算法根据上面两步获得的有限的距离值和部分节点的坐标，计算其余未知节点的机制。由于各种算法采取的策略不同，各种性能参数的区别主要由这一步决定。在分析定位算法时，一般要针对具体情况综合考虑上述3个方面来考察算法性能。

（4）SPA算法

SPA（Self-Positioning Algorithm，自定位算法）是针对没有基础设施的移动无线自组网的算法。它以网络中节点密度最大的地方选取一个参考点作为全局相对坐标系的原点，其余每个节点分别通过测距功能测得邻节点之间的距离值，每个节点在邻节点中选取两个点A、B，选取原则是这两个点本身也是邻节点，并且3个点不在同一直线上。以直线OA作为x轴，以B点在OA上的投影BxB为y轴正方向建立局部相对坐标系。所有的局部坐标系建立完成后，相邻的坐标系通过坐标变换实现坐标统一，最终所有节点都变换成以选取的参考点为原点的坐标系实现定位。由于每个节点都要参与多次的坐标变换，计算量和通信开销都非常大。SPA算法开始是针对无线自组网提出的，未考虑功耗问题，但是用于无线传感器网络中，对于这种通信开销和节点数量呈指数上升的算法需要根据实际情况进行改进。

（5）聚类SPA算法

聚类SPA算法是针对SPA算法通信量过大而提出的改进算法。首先通过运行随机的定时器选取网络中的主节点，主节点一跳范围内的其他节点成为它的从节点。每个主节点使用SPA算法中相似的方法建立局部相对坐标系，并计算得到其余从节点的局部坐标。完成第一步之后，相邻的局部坐标系依据ID号由大到小的原则进行坐标变换，最终以ID号最小的主节点为建立相对坐标原点，从而实现定位。由于算法以节点簇为单位进行坐标变换，计算量和通信量相对SPA算法来说，都得到大幅度减少，基本与节点个数呈线性比例。该算法由于存在簇之间的变换，要求拓扑结构较规则、通信无障碍，故在地形复杂、节点之间通信容易产生冲突的环境下，定位效果不是很好，节点覆盖率也比较低。

（6）Map-growing算法

Map-growing算法是基于测距的算法，其基本思想是通过递归算法，重复进行三边定位实现节点坐标获取。首先在区域节点密度比较大的地方选取一个点O作为相对坐标系的坐标原点。在其邻节点里面选取两个点，选取原则是三点能构成一个良好三角形（3个内角都大于30°）。以其中一个点A作为x轴，另外一个点B确定y轴正方向建立坐标系，B点坐标通过计算可求得，即

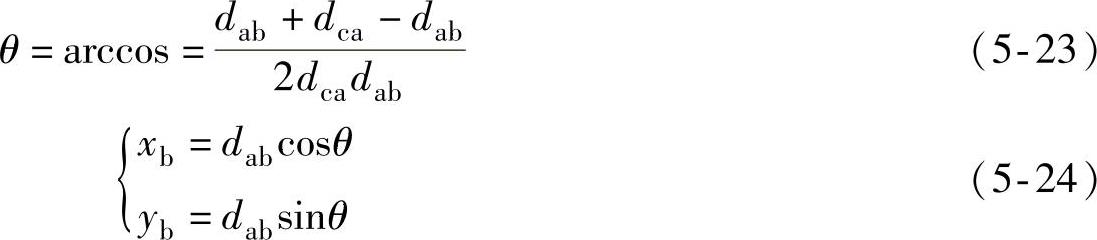
同时与O、A、B三个点为邻节点的未知节点C首先通过三边定位法计算得到自身的相对坐标，计算完成后，也将自身的坐标广播，与B点不是邻节点的D点收到C点发来的坐标消息后，通过O、A、C三个点实现定位并发布消息，重复运行此步，直到所有能计算得到坐标的未知节点都得到定位。

该算法实现简单，只需首先确定3个点建立相对坐标系就可实现区域大部分节点的定位。由于不断升级新的未知节点参与到坐标定位中来，该算法对拓扑结构适应性很强，节点覆盖率高。Map-growing算法是局部定位算法，对于任意一个节点来说，只要其邻节点有3个能确定坐标，它自身的坐标就能确定，并不需要考虑整体布局如何，只要局部区域满足要求，就能实现定位，它适合于节点密度大、地形相对复杂的区域使用。但是该算法使用本身就是经过计算得到坐标的点协助定位，会造成误差累计，一旦测距误差比较大时，距离3个选取的参考点较远的边缘区域节点计算得到的坐标误差就会很大，该算法的准确度有待提高。

（7）LDP算法(www.xing528.com)

LDP算法，同样是一种基于三边定位的相对定位算法。在网络中，选取节点作为网关节点并建立节点簇，簇半径参数k和网关节点的数量依据节点连通度的情况取值。节点经过测距获得邻节点的距离值，大于一跳的节点记录每个网关节点的最小跳数估计距离；每个网关节点采取与Map-growing算法类似的方法建立相对坐标系，并通过三边定位的方式向外扩展，收到两个网关节点信息的未知节点选取距离近的网关节点作为坐标原点计算坐标；每个网关节点建立的坐标系统相互转换，构成一个统一的全局坐标。

该算法在递归调用三边定位的基础上加入了分簇的思想，使得靠近边缘的节点不再由于远离坐标原点而增加误差，每个点都以距离自己比较近的网关节点建立自己的坐标，从而减少了误差累计的影响，提高了定位的准确度。但是不同网关节点之间要进行变换统一坐标，增加了计算量和通信量，并且与Map-growing算法一样，需要在节点密度较高的区域才能获得好的定位效果。

（8）GFF算法

GFF（GPS Free Free）算法其实就是一种Range-free算法。该算法和DV-Hop算法类似，通过两点之间的最小跳数估算这两个点的距离。首先在原点P₁发布一个包[包括坐标（0，0）和自身的ID号]，其余节点相互转发消息。每次转发依此都增加一个跳数。每个节点对同一个数据包，都只接收最小跳数并转发，抛弃跳数大于节点记录跳数的数据包。当P₇接收到这个包时，就以最小跳数d确定x轴。同理，它再向P₃发送包含自身ID号和坐标值（d，0）的DDP包，P₃收到这两个DDP包之后可根据三者之间的距离确定y轴正向。其他的节点n也知道了P₁、P₇、P₃三点之间的距离和每个点到这3个点的跳数，通过三边定位，每个节点能计算得到以跳数表示的相对坐标。

当以跳数代替直线距离时，会产生一定的误差，跳数越多的点，估算的距离值的误差就越大。该算法优势在于无需节点有测距功能，硬件成本低，计算和通信量都较小。由于该算法始终都只有3个节点作为锚节点，因此在节点密度较小的区域，会出现无法与锚节点通信的失效节点，定位准确度严重下降，因此，只有在节点密度高的环境下，此种算法才能有较好定位准确度。

（9）MDS-MAP算法

MDS是多维定标分析方法，最早来源于心理测量学和精神物理学的数据分析技术，指导思想是通过降维方法，在低维数空间中，体现出原来在高维数下的某些特征，从而在低维数条件下进行处理，快速得出所需要的目标值。由于对于任意的两个点之间的参数，若要它们在原来的高维空间中的距离与将维数约简后的低维空间（一维或者是二维）中的距离相同，在低维空间可以重建两点在原来高维空间中的距离特征，体现高维空间的误差信息，这要非常仔细才能完成，否则将产生较大的误差。

MDS-MAP算法将多维定标分析方法运用到节点定位中，通过建立最短距离的相似矩阵确定节点位置，算法主要分为以下3步：

1）从全局网络部署出发，计算所有节点间的最短路径，建立最短路径距离矩阵。如果节点具备测距功能，那么节点间距就是所测距离，如果不基于测距，只知道节点之间的连通度信息，就设节点之间的距离统一为1，然后使用最短路径算法生成节点间距离矩阵。

2）对距离矩阵直接使用MDS标准算法，将其中具有最大特征值的2个或是3个距离矩阵保留下来，建立二维或是三维的相对坐标系统。

3）在拥有足够的已知绝对位置信息的锚节点条件下，将建立的相对坐标系转换为绝对坐标系。

MDS-MAP算法适用于节点密度较大的区域，能基本实现100%的节点定位，但是由于该算法涉及很多的矩阵复杂运算，当节点数目较多时，算法复杂度为0，计算量大，节点耗能也比较大，并且该算法是集中式的，无法应用于需要节点分别计算坐标的区域。当节点连通度较小时，算法测距误差急剧增大，定位覆盖率不高，需要对计算过程有所简化。

3.非基于距离的定位算法

无需测距的算法去掉了节点自身的测距设备，通过跳数或是其他信息估计自身到选定的信标节点的距离值。由于是估计得到的数值，相对于基于测距的算法获得的距离值误差偏大。常用的定位算法有质心法、凸规划算法、DV-Hop算法、DV-Distance算法、Amor-phous算法、MDS-MAP算法和APIT算法等。

（1）质心法

质心法是一种无需测距的粗粒度算法。此算法只需利用锚节点的坐标（x，y）即可估算未知节点的坐标，当未知节点接收到锚节点的位置信息后，用如下公式计算未知节点位置：

（x，y）=（∑x_i/N，∑y_i/N） （5-25）

该算法的最大优点在于算法不需要信标节点和未知节点间的协调，因此算法简单，且容易实现。但是，该算法是假设节点均具有理想的球形无线信号传播模型，而实际上并非如此，而且算法的准确度与信标节点的密度及分布有很大关系，密度越大、分布越均匀，定位准确度越高。但是，对于位于传感器场边缘的未知节点，其定位误差很大。

（2）APIT算法

APIT算法的基本思想：未知节点监听自己附近锚节点的信息，然后从这些锚节点组成的集合中任意选取3个节点。假设集合中有n个节点，那么共有C³_n种不同的选取方法，确定C³_n个不同的三角形，逐一测试未知节点是否位于每个三角形内部，直至穷尽所有的组合。最后，计算包含未知节点所有三角形的重叠区域，将重叠区域的质心作为未知节点的位置。

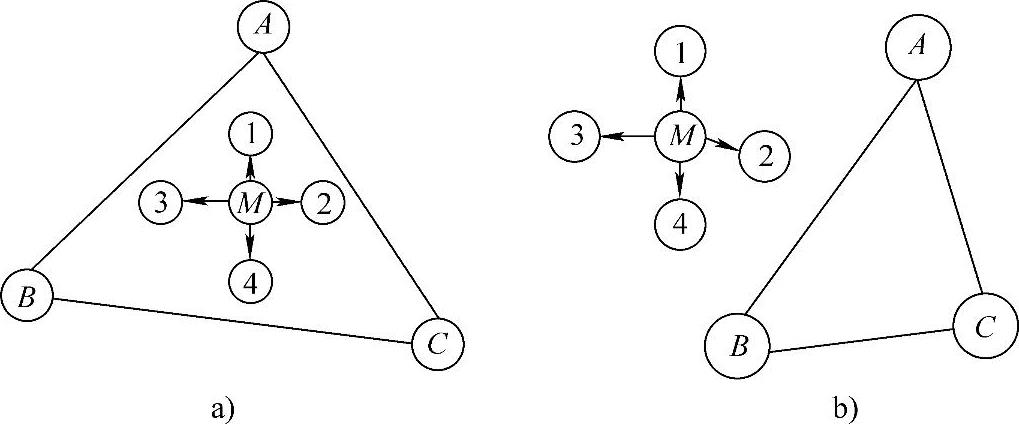
图5-15 APIT定位原理示意图

APIT算法的理论基础是最佳三角形内点测试（Perfect Point-In-Triangulation Test，PIT测试）法。假如存在一个方向，沿着这个方向未知节点M会同时远离或接近三角形的3个端点A、B、C，则M位于△ABC外；否则，M位于△ABC内。

为了在静态网络中执行PIT测试，APIT测试（Approximate PIT Test）应运而生：假设节点M的邻节点没有同时远离/靠近3个锚节点A、B、C，那么，M就在△ABC内；否则，M在△ABC外。APIT算法利用传感器网络较高的节点密度来模拟节点移动，利用无线信号的传播特性来判断是否远离或靠近锚节点。通常在给定方向上，一个节点距锚节点越远，接收信号强度越弱，并通过信息交换来判断与某一锚节点的远近，以此来仿效PIT中的节点移动。APIT定位原理如图5-15a所示，节点M通过与邻节点1交换信息，得知自身若运动至节点1，将远离锚节点B和C，但会接近锚节点A。邻节点2、3和4的通信及判断过程类似，最终确定自身位于△ABC中。在图5-15b中，通过信息交换节点M可知：邻节点3将同时远离锚节点A、B和C，故判断自身不在△ABC中。

（3）DV-Hop算法

DV-Hop（Distance Vector Hop）算法是一种分布式定位算法，属于APS（Adhoc Posi-tioning System）中的一种。在传感器节点通信中，其特点是节点有限，且每节点之间只与邻节点交换信息。此种矢量定位算法符合传感器网络的特点，因此在很多传感网中广泛被采用。

由于在无线传感器网络中常采用距离矢量定位方法，节点间先计算出与信标节点的最小跳数，然后再根据信标节点估算出平均每跳的距离，最后利用最小跳数乘以平均每跳距离，得到目标节点与锚节点之间的估计距离。计算步骤主要分3个阶段：第一阶段，网络中的各个节点采用典型的距离矢量交换协议，使网络中所有节点获得距锚节点的跳数；第二阶段，在获得到其他锚节点位置和相隔跳数后，锚节点计算网络平均每跳距离，然后将其作为一个校正值广播至网络中，目标节点根据其接收到的第一个校正值（对该校正值立即转发，而丢弃之后收到的校正值），以及第一阶段中得到的距各个锚节点跳数来近似计算到各个参考节点的距离；第三阶段，当目标节点获得与3个或更多锚节点的距离之后，利用三边测量法或其变换形式，也即利用GPS定位原理，将GPS中的坐标加时钟同步，求解缩减到二维求解，估计出节点的二维坐标值，实现节点的二维定位。

本算法在不需要测距单元、各向同性的网络中可广泛使用。因为它不需先进行距离的测量，是根据网络的连通性和距离矢量信息的交换，转化为近似的距离测量，方法较为简便。

（4）DV-Distance算法

DV-Distance算法与DV-Hop算法类似，其特点是在距离矢量报文交换阶段，交换的不是节点间的跳数，而是采用RSSI、ToA等方法得到的估计距离之和。由于用节点间估计距离之和来代替两个节点间的直线距离，有过估计的倾向，所以应该利用DV-Hop计算校正值的方法来得到直线距离与折线距离和的大致比例。除此之外的其他步骤，DV-Distance算法和DV-Hop算法相同。

4.基于时间差的节点定位法

网络模型与定位算法：为便于表述，以下将位置已知的节点称为锚节点，待定位的节点称为目标节点。假设传感器节点随机分布在二维监测区域中，3个锚节点A、B与C置于监测区域的外围，坐标分别为（x_a，y_a）、（x_b，y_b）和（x_c，y_c），目标节点坐标为（x，y）。3个基站不共线，每个锚节点可以和目标节点进行单跳RF通信。

锚节点之间以及锚节点与目标节点之间无时间同步的要求。如果待定位的区域很大，3个锚节点无法覆盖，可将区域划分成若干个小区域，分别对每个区域内的节点进行定位。设锚节点A为主站，负责向锚节点B、C和目标节点S发送初始定位信号，其格式见表5-4。锚节点B、C与目标节点S均有局部时钟，用来记录定位信号到达自身的时刻。节点S根据数据包中的“锚节点名称”，可判断是何锚节点发送的定位信号。

表5-4 定位信号格式

5.定位误差分析

当α＜0且γ＞0时，即选择合适的锚节点的位置，就可以对节点进行定位（但坐标的解算准确度受k₁和k₂影响）。从k₁与k₂的表达式来看，其准确度由锚节点B、C和目标节点S局部时钟的测量准确度决定。根据中心极限定理，当测量次数足够多时，k₁、k₂满足N（0，σ²₁）和N（0，σ²₂）分布，且相互独立。利用k²₁/R²≈0、k²₂/R²≈0和k₁k₂/R²≈0，可得以下近似结果：

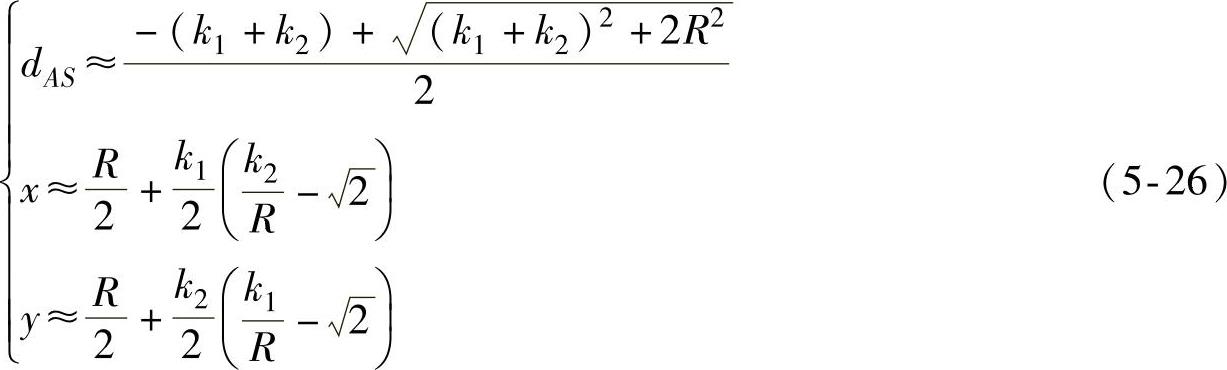
由x与y的方差可知：D（x）=Ex²-E²x=σ²₁[σ²₂/（2R²）+1]/2，D（y）=Ey²-E²y=σ²₂[σ²₁/（2R²）+1]/2。从D（x）和D（y）的表达形式来看，当k₁、k₂不存在测量误差，即σ²₁=σ²₂=0时，位置估计亦不存在误差。当等边直角三角形的边长R→∞时，D（x）=σ²₁/2，D（y）=σ²₂/2。这就意味着在布置锚节点时，可通过增加锚节点间的距离来提高定位准确度。

定位试验法是利用无线传感器网络测试床验证上述定位算法的有效性，其中锚节点与目标节点的配置见表5-5。锚节点采用8位MCU，目标节点由于承担定位算法和与PC的通信，采用16位ARM核的MCU。两种类型的节点均采用3节1.5V的AA电池供电。

锚节点与目标节点的布置：3个锚节点呈等边直角三角形放置，待定位的目标节点放置在3个锚节点的通信范围内，以避免隐终端和暴露终端问题。在试验过程中，固定目标节点的位置，使x=3，y=4，改变三角形的边长R，验证定位准确度与R的关系。

表5-5 锚节点与目标节点的配置