1901年，爱因斯坦的狭义相对论提出并验证

第一章中，我们成功说明了亚里士多德的直观时空观是一个沉重的负担。也就是说空间不是一个固定、不变或绝对的结构，它仅给事物提供一个发生的场所。我们读到了，伽利略已经领会到，持有绝对空间的观念是没有意义的，但他仍坚持绝对时间的观念。上一章中，我们进入了19世纪，接触了法拉第和麦克斯韦的物理学，了解到光是一种电磁场，这是优美的麦克斯韦方程组揭示的。这些都会导致什么结果呢？如果抛弃绝对空间的观念，那么用什么来替代它？绝对时间的观念崩溃又是什么意思呢？我们在本章中给出解答。

毫无疑问，爱因斯坦是现代科学的标志人物。他蓬乱的白发和不穿袜子的样子几乎成了一个“教授”的标准形象。因此出现在孩子画作中的科学家形象经常是一个白发老人。然而，本书中的思想是由一个年轻人提出的。20世纪之交，在思考空间和时间本质时，爱因斯坦才不过20岁出头，他成立了家庭，有一个年轻的妻子。那时，他没在大学或研究机构任职，却经常与几个朋友聚在一起讨论物理问题，时常到深夜。爱因斯坦显得有点远离主流学术团体，现代人倾向于将他视为一个大获全胜的独行侠，这导致一个不幸的后果：这给某些疯子提供了榜样，他们认为自己单枪匹马发现了一种新的宇宙理论，却不明白为什么没有人听他们的。事实上，尽管爱因斯坦的学术生涯开始得并不轻松，但他却与科学界有着非常密切的联系。

令人奇怪的是，他坚持探索那个时代重要的科学问题，却没有取得大学的学术职位。21岁时，他从瑞士联邦理工学院（ETH）毕业，取得了科学和数学专业教师的资格，随后担任了一系列临时教职，为撰写博士论文争取了时间。1901年，在瑞士北部沙夫豪森的一所私立学校任教时，他向苏里奇大学提交了博士论文，却遭到拒绝。那次挫败之后，他搬到了伯尔尼，在瑞士专利局开始了三等技术专家的职业生涯。这时他拥有相对稳定的收入和自由，这成就了他一生中成果最多的几年，历史上任何一个科学家在同样短暂的时间内都无法企及。

这本书主要讲述1905年——“奇迹年”——中，爱因斯坦完成的工作。这一年，他首次写下了E=mc²，并因此获得了博士学位，他完成了一篇关于光电效应的论文，后来他因此获得了诺贝尔奖^[17]。1906年，爱因斯坦还在专利局工作，他因彻底改变我们对宇宙的看法而被提升为二等技术专家。1908年，他终于在伯尔尼获得了一个“合适的”学术职位。这让人忍不住去想，如果那些年，爱因斯坦没有把物理学当作业余爱好，他会取得什么成就？他总是满怀深情地回首伯尔尼的往事。在《上帝难以捉摸》（Subtle Is the Lord）中，爱因斯坦的传记作者兼朋友亚伯拉罕·帕伊斯（Abraham Pais）对爱因斯坦在专利局的日子做出了形容，他写到那是“他最接近人间天堂的日子”，因为他有时间思考物理学。

在通往E=mc²的道路上，爱因斯坦的灵感来自麦克斯韦方程组。它的数学美给他留下了深刻的印象，促使他去认真对待光速不变的结论。光速不变具有科学基础，不具有太大争议，因为麦克斯韦方程组是以法拉第的实验作为基础的。是什么让我们挑起了纷争呢？阻碍我们前进的只是一种偏见，这种偏见使我们无法接受这样的事实，即无论我们以多快的速度追赶，所追物体的速度都保持不变。若你以40英里每小时的速度行驶，此时，一辆汽车以50英里每小时的速度从身旁经过，很明显，你会看到这辆车以10英里每小时的速度开走。如果我们接受爱因斯坦的观点，认为身边的光速不随我们行走的速度而改变，那么前面原本“显而易见”的结论将是一种偏见。我们必须承认常识的误导性，抵制这种偏见，跟随爱因斯坦，看看光速不变会带给我们什么结论。

爱因斯坦狭义相对论的核心是两个假设，用物理的话来说，是两个公理。公理是假定为真的命题。基于公理，我们得以推演出结论，然后，在现实世界中用实验来检验这些结论。运用公理是一个古老的技艺，最早可以追溯到古希腊。采用公理的方法，欧几里得在《几何原本》中发展了一套现在仍在学校讲授的几何体系，其中它对公理方法的应用广为人知。根据5条公设，欧几里得建立了他的几何学，他还认为这5条公设是不言而喻的。然而，随后我们便会看到，欧几里得几何仅仅是许多可能几何体系中的一种，它适用于像桌面这样的平直空间。用来描述地球表面的几何学就不属于欧几里得几何，而是由另一套完全不同的公理定义的。我们很快还会碰到另外一种重要的几何学例子——时空几何学。对照自然检验通过公理得出结论是重要的一个环节，古希腊人没能广泛使用。否则的话，今天的世界会是另外一番景象。早在11世纪，这个简单步骤被穆斯林科学家使用，到16世纪和17世纪已在欧洲生根发芽。最终，在实验的支持下，科学迅速发展，技术的进步和繁荣也随之而来。

爱因斯坦第一个公理是麦克斯韦方程组成立，即无论光源或观察者如何运动，光总是以相同的速度在真空运动。他的第二条公理主张遵循伽利略的说法，即任何实验都不能用来标识绝对运动。有了这两个命题作为武装，我们就可以像优秀的物理学家那样继续去探索了。爱因斯坦的理论源于他的两个公理，理论的最终检验标准却是它预测和解释实验结果的能力，科学一向如此。搬用费曼的话来说：“概括起来讲，我们通过以下步骤寻找新的规律。首先，猜猜看。然后，基于猜测计算出结果，看看这个基于猜测的定律后面蕴含的结论。接着，将结果与大自然、实验或经验进行对比，通过与观测结果直接对比来判断猜测是否可行。如果与实验不一致，那么理论就猜错了。这简短的一句话是科学的关键。这跟你的猜测有多美没有关系，跟你多聪明，你是谁，叫什么也没关系。只要与实验不符，就是错的。就是这样。”这则绝妙的话摘录于费曼在1964年的一次演讲，我们建议读者在网络上搜索演讲视频观看。

接下来几页的目标是找出爱因斯坦公理内含的结论。我们的工具是思想实验，一种爱因斯坦经常喜欢使用的技术。具体说来，假定无论观察者怎样相对运动，光速相对于所有观察者都保持不变，我们探讨这一假定导致的结果。为此，想想一种叫作光钟的笨重钟表，它由两个镜子组成，镜子间，一束光来回反射，光束反射一次，光钟走动一下。例如，如果镜子相距1米，则光大约需要6.67纳秒完成一次往返^[18]。一次往返，光以299792458米每秒的速度移动了2米，您可以亲自检查下这个数字。这是一个高精度的时钟，一个心跳的时间，它走了1.5亿下。

现在，把光钟放在一列火车上，随火车从站台上的人身边疾驰而过。重要的问题是，对站台上的人来说，时钟走多快？在爱因斯坦之前，人们假定时钟快慢是不变的，即每走一步需要6.67纳秒。

图2显示了光钟在火车上的一个时间单位，它是由站在站台上的人观察到的。因为火车正在前进，在一个时间单位内，光必须传播更长的距离。也就是说，在站台上的人看来，由于时钟的运动，在一个时间单位内，光束的起点和终点落在了不同的地方。因此，若要使光钟与它静止时走动的快慢相同，光必须传播得快一点，否则，它无法在6.67纳秒内走完这段被拉长的距离。在牛顿世界里，火车的运动增加了光速。但关键是，爱因斯坦认为光不能加速，它对每个人都一样。这引起一个令人不安的结果，即对站台上的人来说，由于光线要走更长的距离，移动的光钟每走一步都要花费更长的时间。这个思想实验表明，若光速如麦克斯韦所说的是一个不变的常数，那么时间将以不同的速率流逝，其流逝的快慢由物体相对于我们的运动状态来确定。换句话说，绝对时间与光速不变水火不容。

必须强调的是，时钟变慢并非光钟所特有的现象。普通的摆钟和光钟没有本质区别，只不过它的工作原理是每一秒钟摆在两个地方“往返”一次。原子钟也是这样，它通过原子发出光波的波峰和波谷的数目来确定一个时间单位。甚至，体内细胞的衰变率也可以用来计时。这些装置都测量了时间的流逝，会得到同样的结论。光钟常常被用来讲授爱因斯坦理论，不厌其烦，但这是一种非常陌生的时钟，引起了无数困惑。我们很容易被误导，认为以上结论是光钟独有的奇怪特性，而不是我们对时间本身的本质认识。若这样认为，那就大错特错了。选择光钟而不是其他时钟的唯一原因是，满足使用爱因斯坦光速不变的奇怪要求，从而让每位读者都能得到有关相对时间的结论。然而，通过对光钟思考而得到的所有结论都适用于任何其他类型的钟表。原因如下。想象一下，把自己放在一个密闭箱子里，在箱子里放入一个光钟和一个摆钟，给它们校准时间。若这两个钟表足够精确，它们将保持同步，并永远显示相同的示数。接下来，把箱子放到运动的火车上，由爱因斯坦第二公理，箱子里的人不能判断自己是否在运动。但若认为光钟和摆钟不同，它们不再同步，那么箱子里的人就可以肯定自己的运动状态，这违背第二公理的结论^[19]。因此，摆钟和光钟必有完全相同的时间规律，对站上的人来说，运动的光钟变慢，那么其他运动的时钟也将变慢。实际上，站台上的观察者看到的是移动的火车上时间流逝变慢。这不是幻觉引起的。

因此，我们必须做出选择，要么坚持绝对时间这一令人舒服的概念，但要抛弃麦克斯韦方程，要么抛弃绝对时间，支持麦克斯韦和爱因斯坦。该如何选择呢？如果想证明爱因斯坦是对的，必须找到这样一个实验，通过该实验在运动的物体上观察到变慢的时间。为了设计这个实验，首先需要确定物体速度达到多大时，才能出现明显的效果。显然，高速路上70英里每小时的车速，并不能使时间慢下来，否则，我们开车去一次商店，回家后会发现自己的孩子变得比我们老。这很荒谬，但爱因斯坦的理论确实如此，如果我们能够以足够快的速度旅行，那么就能看到因运动引起的年岁差别。足够快是多快呢？在站台上的人看来，光沿着图2中三角形两斜边传播。爱因斯坦论述，因为光比它在静止的光钟中传播的距离要远，时间单位变长了，时间的流逝就变慢了。接下来，要做的是计算时间变长了多少（给定列车的速度的情况下）。毕达哥拉斯^[20]可以帮助我们完成这一任务。

若不想看数学，你可以跳过下一段，但你必须相信，任何人都能算出最后的数值。书中碰到的其他数学问题也一样，跳过它，别担心。尽管数学有助于更深入地理解物理，但撇开它们，本书一样可以读懂。若你以前没有任何数学经验，或许你能跟着学一学。在这里，数学问题已经变得相当容易，你只要不抵触它就好，一些常见的脑筋急转弯都比我们的数学难。说来说去，数学可能是读懂本书的一个小挑战，但是值得去努力尝试。

回到图2，对站台上的人来说，一个时间单位的一半是光从底部反射镜传播到顶部反射镜所用的时间，假设它等于T。我们先找到T，然后让它翻倍，就得到了整个时间单位的长度。知道T之后，我们可以计算出三角形最长边（斜边）的长度cT，即光速（c）乘以光从底镜到顶镜所用的时间（T）。请记住这样一个定义，物体通过的距离等于物体的速度乘以运动的时间。例如，一辆汽车以60英里每小时的速度在一小时内行驶的距离是60×1=60英里。算出两个小时走过的路程也不难，你只需调用公式“距离=速度×时间”。知道T之后，我们还可以计算出时钟在半个时间单位中移动了多远。若火车以v的速度移动，那么仅仅调用公式“距离=速度×时间”，就可以得到在半个时间单位中光钟移动的距离是vT，这个距离是三角形底边的长度。因为我们已经表示出最长边的长度^[21]，因此，只需使用下勾股定理就可以找到它与镜间间距的关系。已知镜子间间距为1米，根据勾股定理就有(cT)²=1²+(vT)²。在数学中，圆括号表示计算操作的先后顺序，例如，公式中(vT)²表示：“首先把v乘以T，然后给它的结果求平方。”仅此而已。

知道光速c，火车的速度v，T就可以从公式中得出来了。最粗暴的方法就是猜测了，猜一个T的值，看它是否满足方程。大部分猜测都是错的，你需要一遍一遍地尝试，一番操作后就可以找到答案。这个过程很烦琐。幸运的是，我们可以通过“解”方程来避免这个烦琐的过程。此方程可以表示为T²=1/(c²-v²)，其中，斜杠用来表示“除以”，如，1/2=0.5，再如，a/b表示“a除以b”。上式的意思是“先算出c²-v²，然后再用1除以它。这样我们就得到了T²的值了。如果你有一些数学基础，这确实有些无聊。如果你没有数学基础，不能理解为什么T²=1/(c²-v²)，不用去管它，请相信结论，或者往公式里代入些数值验证下。得到T²的结果，也就是“T乘以T”的结果，然后通过对结果求平方根就可以得到T的值。在数学里，一个数的平方根是这样定义的：一个数的平方根乘以它自身，等于这个数。例如，9的平方根是3，7的平方根接近于2.646。大多数计算器有计算平方根的功能。一个数的平方根通常由符号“”表示，如。求平方和求平方根互为逆运算，如4²=16，。

回到我们的问题上来，有了以上数学基础，对站台上的人来说，光钟的一个时间单位就可以轻松获取了。光从底部反射镜到达顶部反射镜并再次返回所需要的时间是2T。首先对T²求平方根，然后乘以2，就可以得到。在知道火车的速度v、光速c以及两个镜子之间的距离（1米）的情况下，该公式就能计算出站台人员观测到的时间单位。对于火车上光钟旁的观察者来说，这个过程光仅是以速度c运动了2米（因为距离=速度×时间，所以时间=距离/速度），所以光钟一个时间单位仅等于2/c。站台上的人观测到火车上的光钟变慢了，变慢了多少可以通过以上两个时间单位的比值得出。简单计算表明，光钟变慢由系数表示。重新整理得到，。这个常数用希腊字母γ表示，它的发音为“gamma”^[22]，是相对论中一个非常重要的数值。通过观察可以发现，只要光钟速度低于光速，由于v/c小于1，γ总是大于1。此外，当光钟速度远小于光速时（生活中常见的速度，对驾驶员来说，光速是6.17亿英里/小时），γ非常接近1。只有当光钟速度与光速可比拟时，γ才明显偏离1。

讲到这里，我们成功确定了对于站台上的观察者，飞驰火车上的时钟变慢了多少，所需相关数学也已讲述完毕。让我们根据情况代入数据看一看。如果火车以300千米每小时的速度行驶，那么不难发现v²/c²是一个非常小的数字，0.000000000000077，继续通过算式=1.000000000000039，便得到了“时间拉伸”因子γ。不出所料这是一个微乎其微的影响。在站台上的朋友看来，乘火车旅行100年，你的寿命只会延长0.000000000000039年，这个数字略高于十分之一毫秒。然而，当火车以90%光速的速度疾驰而过时，情况就不同了。这时，时间拉伸因子将大于2，也就是说坐在站台上的人看到，移动的时钟的摆动频率不到车站上时钟的一半。这就是爱因斯坦的预言，有点难以置信。不过对优秀科学家来说，能否相信它要看实验检验。

接下来会讨论验证这一结论的实验，但在此之前，我们停一停，进一步思考下刚刚得到的结果。我们坐在光钟旁边，从火车上乘客的角度出发，再做一次思想实验。对乘客来说，时钟没有运动，光只是上下运动，这就像我们坐在咖啡馆里看到身边的时钟一样。根据伽利略的说法，光钟相对于乘客静止，乘客肯定会看到光钟每6.67纳秒走一个时间单位，心跳一次，它走1.5亿次。与此同时，对站台上的观察者来说，火车上的光钟用了6.67纳秒多一点的时间来完成一个时间步。在数过1.5亿次时间单位后，他的心跳略多于一次。在站台上的人看来，他比坐在火车上的乘客衰老得快。这是很惊人的结论。(www.xing528.com)

我们刚刚已证明，对于真实的火车来说，其速度远不及光速，这种影响微乎其微，但它确实存在。在一个想象的世界里，火车以接近光速的速度在一条长长的轨道上疾驰，这种效果将被放大，以至于站在月台上的人会感觉到自己变老得快些。

在实验室，若要测试到这种否定绝对时间的结果，就需要发展一种方法来研究接近光速运动的物体。因为，只有物体接近光速，时间拉伸因子γ才足以被实验测量到。稍微理想一些，我们寻找一个有寿命的物质来做研究，看看可否通过让它快速运动起来来延长它的寿命。

幸运的是，这样的物质确实存在，科学家对它们再熟悉不过了。事实上，我们本身就是由这些物质构成。它们就是基本粒子，一种非常小的亚原子粒子，宇宙中所有物体的最小组成部分。它们因为小，所以很容易被加速到很大的速度。在本书的后面，我们还会看到很多有关基本粒子的内容。现在，我们给出两个基本粒子，即电子和μ子。

电子是构成我们身体的重要粒子，我们应该感激它们。电子参与导电，当它们通过电线时，点亮灯泡，加热烤箱。μ子在许多方面与电子相同，只是质量更大些。科学家并不理解为什么自然界会存在μ子，它更像是电子的副本，却不参与地球和人类的构造。不管μ子存在的原因是什么，它在检验爱因斯坦相对论方面表现非常出色。因为它的寿命很短，而且质量很小，很容易加速到很大的速度。据我们所知，把一个μ子放在身边时，它的寿命大约是2.2微秒（一微秒是百万分之一秒），相比μ子，电子的寿命很长，没有限制。μ子死亡时，变成一个电子和一对叫作中微子的亚原子粒子。这里，我们只需要知道μ子死亡就可以了，不需要其他额外信息。在纽约长岛，有一个布鲁克海文国家实验室^[23]，实验室内有一台交替梯度同步加速器（AGS），这台设施为爱因斯坦理论的验证提供了了不起的实验。上世纪90年代末，布鲁克海文的科学家们制造了这台机器，他们产生一个μ子束，μ子以光速的99.94%在14米直径的圆环上循环。如果μ子在圆环中只能存活2.2微秒，那么它们只能跑15圈^[24]。实际上，它们跑了400圈，这说明它们的寿命延长了29倍，达到60多微秒。实验事实说明爱因斯坦是对的，他走在真理的道路上。但他的理论能有多准确？

本章前面所讲的数学将在这里发挥作用了。我们刚才用它精确预测了以恒定速度运动的时钟比静止时钟变慢多少。因此，这里我们可以通过数学公式预测，当μ子以99.94%的光速运动时，时间会减慢多少，寿命又会延长多少。根据爱因斯坦理论，布鲁克海文μ子的时间将延长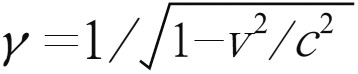倍，其中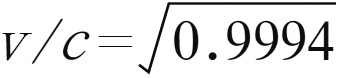。按下手边的计算器，验证下，你会发现γ等于29，和布鲁克海文的实验人员发现的完全一样。

我们值得在这里稍作停留，思考下发生了什么。根据勾股定理和爱因斯坦关于光速不变的假定，我们导出了一个数学公式。它赋予我们预测亚原子粒子寿命延长的能力。当一个称为μ子的亚原子粒子在布鲁克海文的粒子加速器中加速到99.94%光速的速度时，我们计算出它的寿命应该是静止μ子寿命的29倍。这一预测与布鲁克海文的科学家所测到的数值完全一致。这就是物理学的天地，你思考得越多，它就越精彩。当然，在20世纪90年代，爱因斯坦的理论早已成熟。布鲁克海文的科学家们更关注μ子的其他性质。爱因斯坦理论的寿命延长效应给他们提供了额外的好处，这意味着他们有了更多的时间对μ子进行观察。

根据实验，我们不得不得出这样的结论：时间是可拉伸的。它流失的快慢因人而异（因μ子而异），取决于他们的运动状态。

嗅觉敏锐的读者可能已经发现，时间这种令人不安的行为似乎不是问题的全貌，还有其他东西潜藏在后面。回到交替梯度同步加速器中，再想一想那些嗡嗡作响的μ子。在加速器上画一条终点线，数一数μ子在死亡前跨越终点线的次数。对于观察μ子的人来说，由于μ子寿命延长了，它们跨越了400次。但如果和μ子一起绕环疾驰，你会跨越终点线几次呢？必须是400，否则这个世界将毫无意义。问题来了，当你随着μ子绕环飞行时，手表会显示它们的寿命只有2.2微秒，因为μ子相对于你是静止的，并且μ子静止时的寿命只有2.2微秒。尽管如此，在μ子消失前，你和μ子还必须绕环运动400多圈。然而，在2.2微秒内跑400圈似乎又是不可能的。这是怎么回事？幸运的是，有办法摆脱这种困境。从μ子的角度来看，环的周长缩小了。为了观测的一致性，从μ子看来，环的长度必须收缩，直到它产生的效果和μ子寿命增加的相同。所以空间也必须是可伸缩的！跟时间膨胀一样，空间收缩也是一个真实的效果。运动的物体确实如此。举一个奇怪的例子，有一辆4米长的汽车试图进入一个3.9米长的车库，这似乎不可能。但根据爱因斯坦理论，如果汽车的速度超过光速的22%，它就能挤进去，至少在碰到墙的最后一刹那。同样，根据数学公式，你可以验证22%是正确的数字。因为，再快一点，车子就缩小到3.9米以下；再慢一点，车身缩小的长度不够。

在亚原子世界，发现时间减慢，距离缩短，就足以令人惊讶了，更何况爱因斯坦的推理对人类这样大小的物体也适用。有朝一日，我们的生存将依靠这些奇怪的现象。想象一下几十亿年后的遥远未来，太阳不再能给我们提供生命所需的稳定光照，它已变成了一个恒星怪物，会在最后死亡的暴胀中，吞没掉我们的星球。那时，如果我们没有因其他原因而灭绝，就必须设法逃离地球家园，前往其他行星。然而，人类生活的银河系是由1000亿个太阳组成的螺旋状岛屿，直径约10万光年。也就是说，在地球上看来，光需要10万年才能穿过银河系。若如上所述，前往其他行星是我们最终的命运，那么我们的目的地似乎也只能局限于临近的一小部分恒星（天文尺度上），因为好像我们很难指望达到银河系更遥远的角落，即便光也需要10万年的时间。事实并非如此，爱因斯坦的理论可以拯救我们。我们可以建造一艘飞船，以非常接近光速的速度飞向太空，那么恒星间的距离就会缩短。我们越接近光速，间距就越短。如果我们能以99.99999999%的光速旅行，那么我们就可以用短短的50年时间离开银河系，飞到邻近的仙女座星系，尽管它距离我们将近300万光年。这是一项艰巨的任务，最大的障碍是如何为宇宙飞船提供动力，使其能够达到如此快的速度。随着空间和时间扭曲的发现，前去宇宙远处旅行的想法和以前已大不相同。如果你是人类第一批仙女座探险队的一员，经历了50年的旅程后来到了新的星系，并在那里给出生的孩子讲太空中蓝色星球的故事，若这些新生的小孩希望回到地球家园，亲眼一睹它的姿态，他们需要调转宇宙飞船，再花上50年才能返回地球。这样，往返仙女座的整个旅程将花费100年的时间。然而，更令人震惊的是，当他们回到地球轨道时，地球上的居民已经生活了600万年了。那时，他们祖先的文明是否还存在？爱因斯坦让我们看到一个匪夷所思的世界。

[17]因在数学物理方面的成就，尤其是发现了光电效应的规律，爱因斯坦获得了1921年度的诺贝尔物理学奖。

[18]1纳秒是千分之一微秒，即0.000000001秒。（原书注）

[19]设定密闭的箱子是为了防止产生这样的想法，即，通过观看窗外的世界来确定我们是否在运动。事实上，即便看到外面也是没用的，通过向外看你只能确定自己是相对于地面在运动。（原书注）

[20]这里指的是勾股定理。

[21]被表示为cT。

[22]中文注音：伽马。

[23]布鲁克海文国家实验室(BNL)位于纽约长岛萨福尔克县中部，成立于1947年。历史上该实验室曾经有7个项目12人次获得过诺贝尔奖，是世界著名的大型综合性科学研究基地。

[24]利用圆的周长等于π乘以直径，其中π约等于3.142时，你可以自己验证下。（原书注）