维数是人们熟悉的几何学基本概念,如零维的点、一维的直线、二维的平面、三维的空间。但在自然界和工程中却有许多现象难于用传统的概念作出回答。如雪花、彩云、花朵、大气湍流、粉粒形状、粗糙表面的表面粗糙度等,对这些现象最多只能加以定性描述。分数维图形则将给出定量分析,用分维加以表示。分维图形可以表征广泛存在于自然界的一个大类无序、复杂、奇异的客体。因为从分维的角度看空间是连续的,也就是空间维数不是从0到1、从1到2、从2到3跳跃式地变化,而是可以连续地变化,即可以是整数,也可以是分数,通过具体计算所确定的维数称为豪斯道夫维数,记为Df。
取一个边长为单位长的正方形,若每边放大2倍,则正方形面积放大4倍,其数学表达式为22=4,这是2维图形。对于3维图形,取一个棱长为单位长度的立方体,若每条棱边的长度放大2倍,则立方体体积放大8倍,其数学表达式为23=8。依此,对于一个Df维的几何对象,若每个棱边长度都放大L倍,则这个几何对象相应地放大K倍,归纳上述结果,Df、L和K三者的关系为
LDf=K (11-1)
取对数则有

式(11-2)中Df不必是整数,对具有奇异构形的分形结构,体系的维数一般为分数,只有个别情形是整数。上面是从放大几何对象来考虑分数维的,也可以从缩小几何对象定义分数维。如图11-3所示,假定有单位正方形,把它等分为4个小正方形,每个小正方形相对原来的单位正方形每边缩小为原来的 ,然而4个小正方总的面积仍为原单位正方形的面积,既有
,然而4个小正方总的面积仍为原单位正方形的面积,既有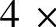
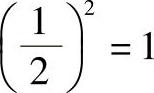 ,取对数就成为
,取对数就成为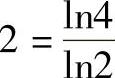 ,这里2正是该几何图形的维数。
,这里2正是该几何图形的维数。
现在,把一个Df维的几何对象等分成N个小的几何图形,则每个小图形每维缩小为原来的r,而N个小图形的综合应为NrDf=1,所以分维数为


图11-3 分数维定义
图11-3所示为等分后的单位图形数,直线为2,正方形为4,立方体为8,则N和r的关系为直线 
正方形 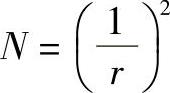
立方体  (https://www.xing528.com)
(https://www.xing528.com)
如图11-4所示,Koch曲线的构造方法是把一直线三等分,去掉中间一段,并补进两条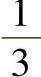 直线长度的线段,经无限重复而得的自相似图形。按上述分析可知,这时单位长度
直线长度的线段,经无限重复而得的自相似图形。按上述分析可知,这时单位长度 ,单位图形N=4,故有
,单位图形N=4,故有
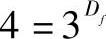
所以
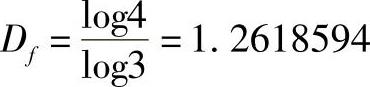
这种Koch曲线的构造是有规则的,它具有严格的自相似形,Koch曲线处处连续,但处处不可微,它是一个分维图形。构造Koch雪花与折线的构造相似,以一个三角形为源多边形,即初始元,如图11-5a所示,将三角形的每一边三等分,舍去中间的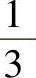 ,然后按生成规则产生初始元。图11-5b、c所示是Koch雪花的形成过程。
,然后按生成规则产生初始元。图11-5b、c所示是Koch雪花的形成过程。
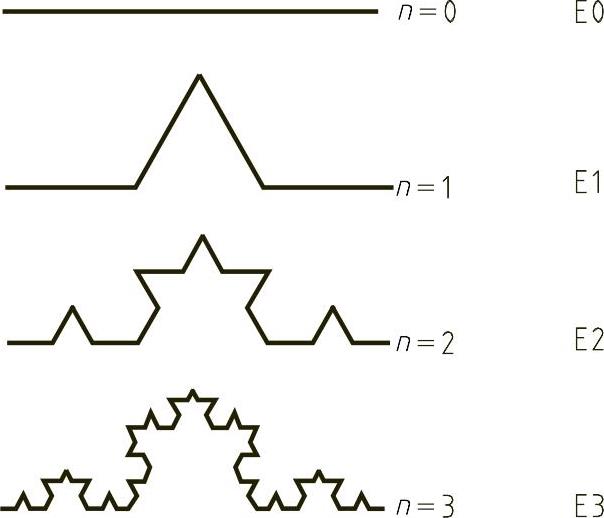
图11-4 Koch曲线的构造方法
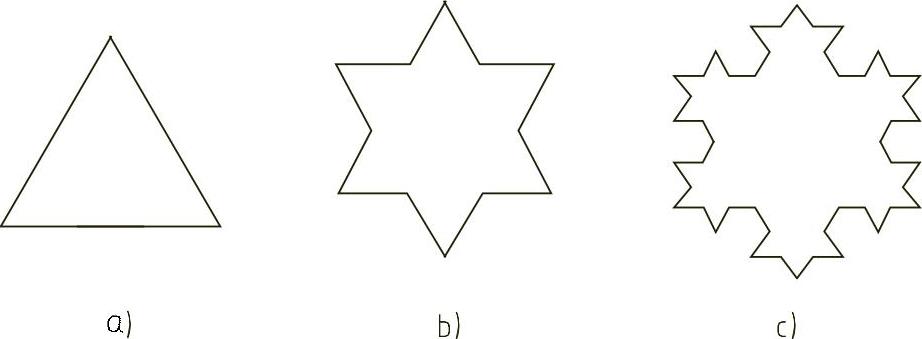
图11-5 Koch雪花的形成过程
从源多边形(三角形)开始,第一步形成六角星形,第二步是将六角星的12条直线边按Koch曲线生成规则进行同样的操作,依次类推,直至无穷,在极限情况下,折线成为曲线,组成曲线的各个折线趋于无穷小,所以它虽是处处连续的,但处处无切线,不可微。因为雪花的构造过程每一步演变都使折线的长度增加,所以在极限情况下Koch雪花的轮廓线总长度趋于无穷。可是,它是一条闭合曲线,因此雪花面积有一个确定的值,通过简单的计算,有
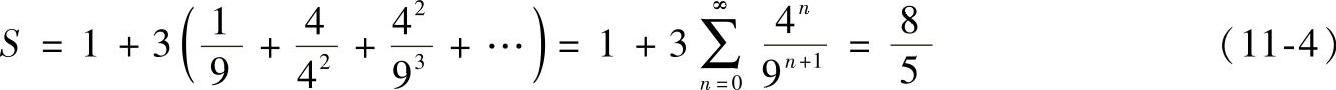
这里n=0相当于图形演变过程的第一步,n=1为第二步,以此类推。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




