计算机实验工程图形学：回转薄壳的主曲率半径

图9-31所示为一空间曲面Σ，其上有一点P，过P点在该曲面上作任意两条曲线c₁和c₂，在P点分别作这两条曲线的切线t₁和t₂，t₁和t₂组成一平面T，T即是曲面Σ在P点的切平面，过P点作该切平面的垂线n，n即为曲面在P点的法线。过该法线可以作无数个平面，它们均与空间曲面相交，产生无数条平面曲线，在这些平面曲线中，它们在P点的曲率半径有一最大值和一最小值，也就是曲面在P点的两个主曲率半径——第一曲率半径R₁和第二曲率半径R₂。

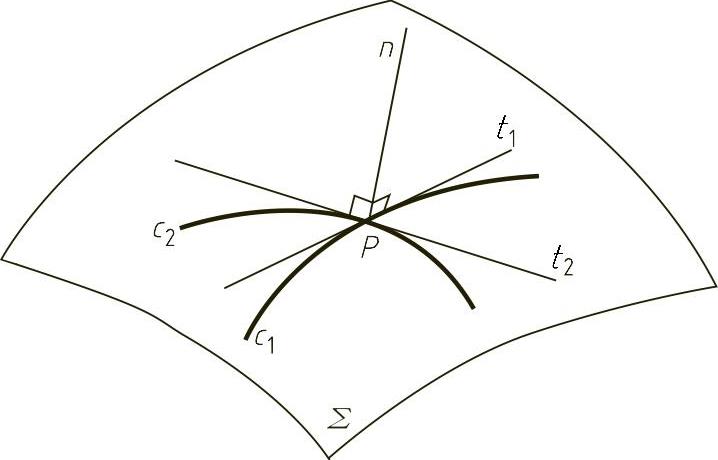
图9-31 空间曲面

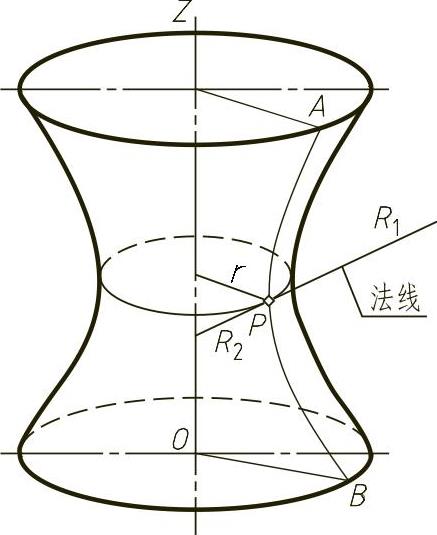
图9-32 回转曲面

如图9-32所示，设平面曲线AB绕同平面中的OZ轴旋转形成一个回转曲面，曲线AB称为该回转曲面的母线，又称为经线。设P为经线上一点，它与轴所构成的平面与曲面的交线（即经线）在该点处的曲率，称为第一主曲率，其倒数为第一主曲率半径R₁。回转面上P点的法线延长线与轴的交点与P点之间的距离称为第二主曲率半径R₂。

过P点作垂直于OZ轴的平面与壳体中面相交得到一个平行圆，它的半径记为r。

可以发现，回转曲面上处于同一平行圆上的点其第一主曲率半径和第二主曲率半径保持不变。

下面利用投影图，分析常见回转曲面的主曲率半径、回转曲面上某一点的纬圆半径r_k，以及曲面经向线上某点切线与旋转轴的夹角ϕ。

1.圆柱面

设圆柱面的直径为D，其投影如图9-33所示。根据上述分析，由图可知，圆柱面上任一点P（p，p′）的主曲率半径为

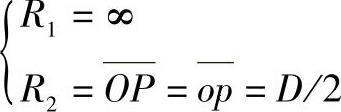
2.圆锥面

设圆锥面的顶角为2θ，其投影如图9-34所示。锥面上任意一点P（p，p′）所在平行圆半径为r，由投影图可以看出，P点的两个主曲率半径为

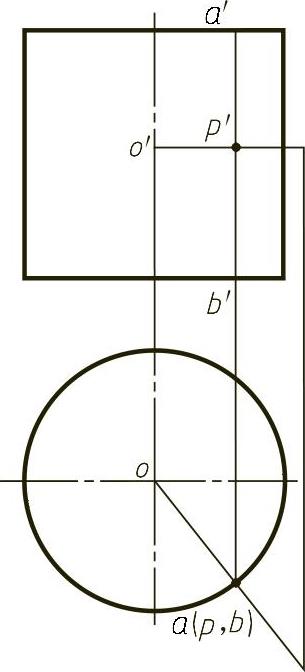
图9-33 圆柱面的投影

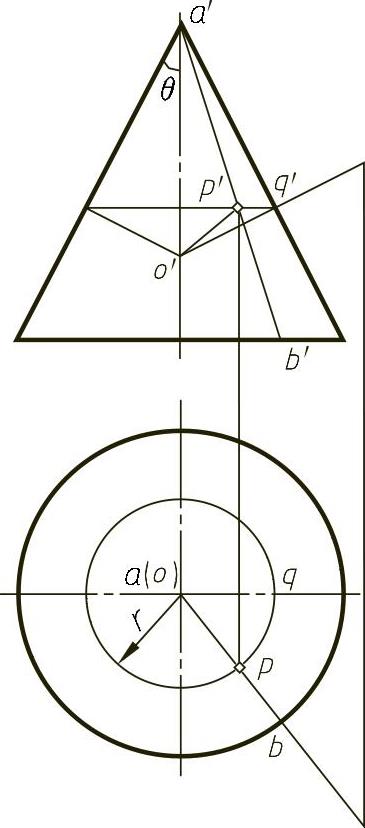
图9-34 圆锥面的投影

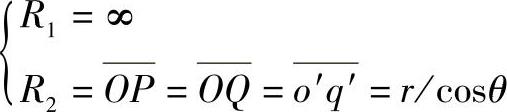
3.球面

设球面直径为D，其投影如图9-35所示。球面上任一点P（p，p′）的两个主曲率半径可从投影图看出应为

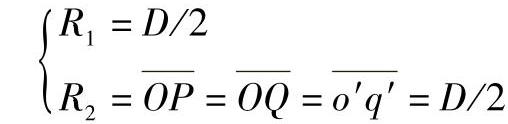
4.回转椭球面

设椭圆的长轴为2a，短轴为2b，其投影如图9-36所示。回转椭球面上任一点P（p，p′）所在的经线为一椭圆，其方程为

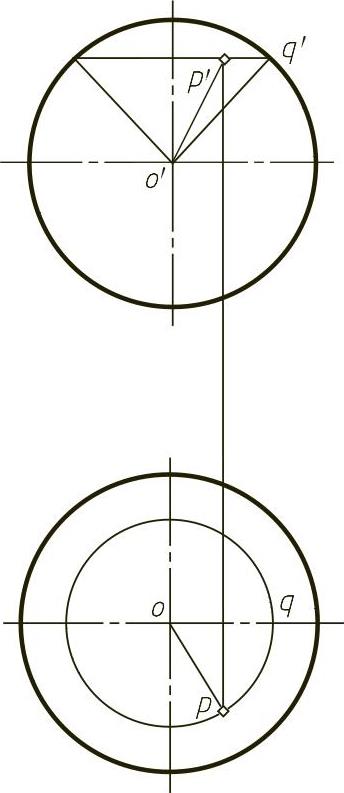
图9-35 球面的投影

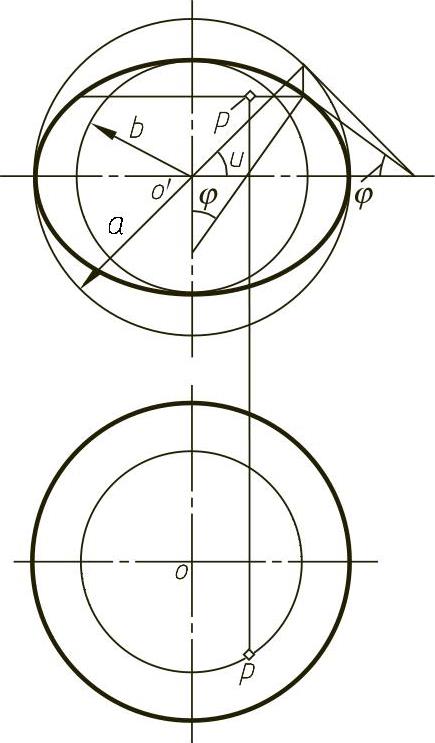
图9-36 回转椭球面的投影

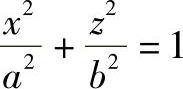
由投影图可得

x=acosu(www.xing528.com)

z=bsinu

x′=-asinu

z′=bcosu

x″=-acosu

z″=-bsinu

由高等数学可知

又由投影图可得

而

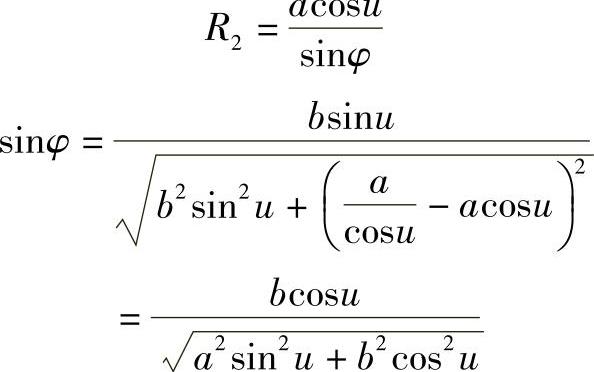
所以

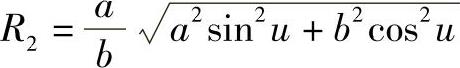
由此可以看出，回转椭球面上点的第一、第二主曲率半径R₁、R₂随着u的变化而变化。

根据式（9-64），当容器材料选定后，按第三强度理论进行设计，使许用应力[σ]小于σ₁、σ₂中的大者，即可得出壁厚计算公式。在不考虑焊缝系数和腐蚀裕量的条件下，球罐的壁厚计算公式为

式中 p——内压力；

D——球面直径；

[σ]——材料许用应力。

椭圆形封头壁厚计算公式为

式中 p——内压力；

a——椭圆形封头长半轴；

c——短半轴；

[σ]——材料许用应力。

圆环管道壁厚计算公式为

式中 p——内压力；

r——母线圆半径；

R——母线圆圆心旋转轨迹圆半径；

[σ]——材料许用应力。