用部分圆锥面代替部分球面展开：实现惊艳图形

由于用部分圆锥面法展开球面，每一份的面积均不相等，因此不能仿照圆柱或椭圆柱面的方法来求展开图形的面积，只能建立求某一块展开面积的通式，然后求其总和，如图9-20所示。

图9-20 以圆锥面代替部分球面展开

LP9-7.lsp程序

由图9-20可知，每一块圆台的面积为

A=π（R_i+R_i+1）L （9-38）

式中各参数为

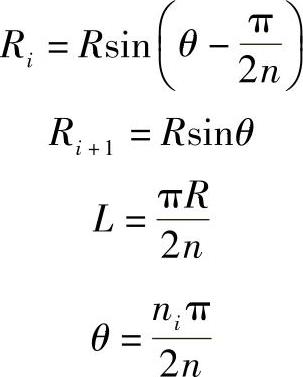
而n为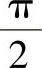角度的等分数，与A_i份数一致，n_i为第几份，球面份数为2n。将各参数代入式（9-38）并整理得

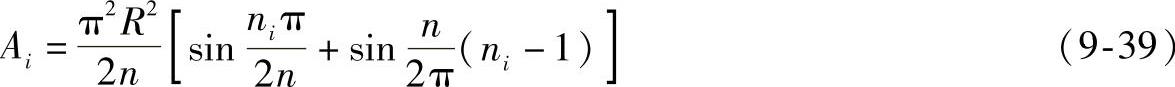
用部分圆锥面近似代替部分球面进行展开的程序LP9-7.lsp，可通过扫描二维码观看。

1.近似展开方法合理性的第一判断标准

以面积为判断标准，对三种近似展开方法进行比较。在不同份数下，用不同方法展开的每块球面的展开面积与相应份数下每块真实球面表面积的比较见表9-2。

表9-2 近似展开面积与真实面积对比

在不同份数下，用部分圆锥面法展开的球的总展开面积见表9-3。

表9-3 用部分圆锥面法展开的球的总展开面积

以12等分（或12份数）球面为例，利用各种展开方法所得面积和其理论面积分别为

A_理论=4πR²=12.566R²

A_圆柱=12.852R²

A_椭圆=12.276R²

A_圆锥=12.496R²

通过各种近似展开面积与真实面积的比较可以得出以下结论：

1）近似展开方法得到的展开面积与球的真实面积之比取决于对球面的等分数n，而与球半径R无关。n越大，近似展开所得的面积越接近于真实表面积。

2）从制造角度出发，并非等分数（或份数）越多越好，而应在一定的允许误差条件下，确定适当的等分数（或份数）。

3）从三种近似展开方法比较来看，用圆锥面近似展开方法所得的球的总展开面积更接近于真实球面的总表面积。

4）从冲压成形的角度考虑，球面展开以采用椭圆柱面法较好。

2.近似展开方法合理性的第二判断标准

（1）球体理论容积 设球形容器半径为R，原料深度为H，求原料所占体积V。所求体积为两部分之差，设整个球体体积为V₂，H深度以上部分体积为V₁，则V=V₂-V₁。与Z轴垂直的截平面截球得一圆，截平面的位置由参数u控制，如图9-21所示。而截断圆的半径r也为u的函数，有

r=Rcosu （9-40）

故截断面的面积为

A=πr²=πR²cos²u （9-41）

又因截平面的高度为

z=Rsinu

dz=Rcosudu （9-42）

所以有

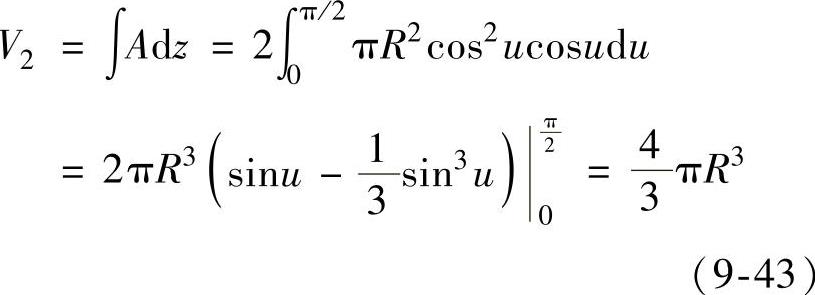
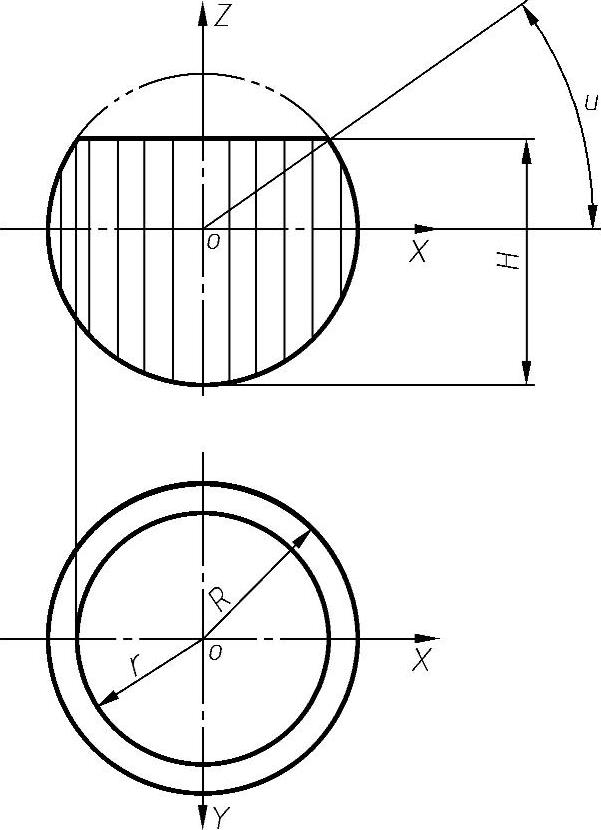
图9-21 球形容器投影示意图

而

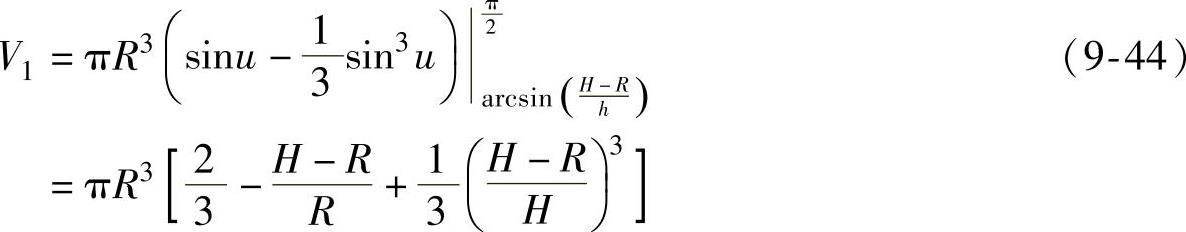(www.xing528.com)

得

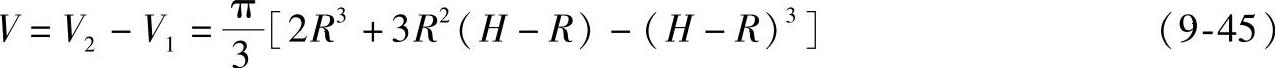
（2）圆柱面法展开球面的容积误差 图9-22所示为部分圆柱的两面投影，用平面π截切此部分圆柱面，得截断面面积为

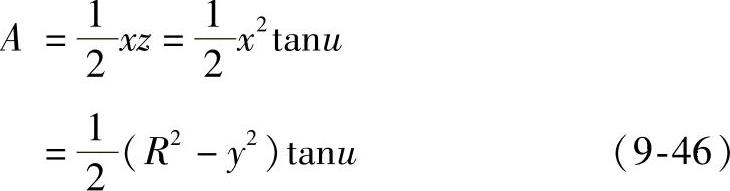
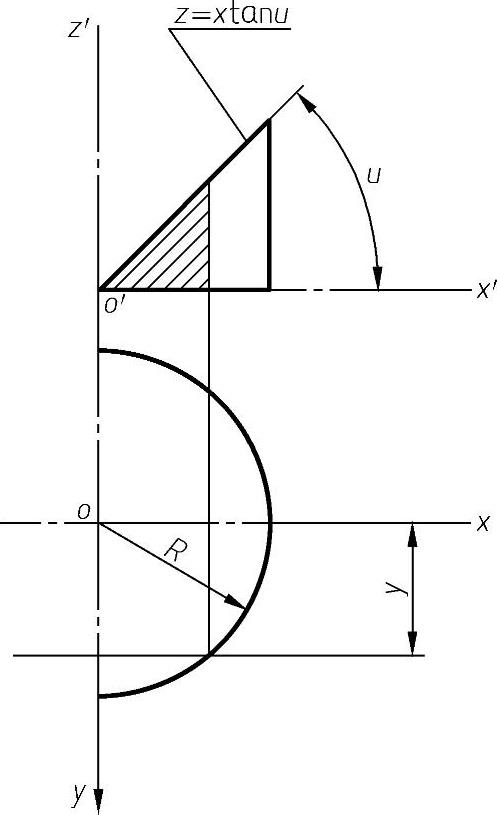
图9-22 部分圆柱面的两面投影

所以此部分圆柱体体积为

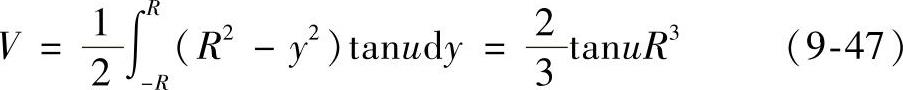
当u=15°，即12等分球面时，由式（9-47）可得展开容积为4.287187R³。而球体的理论容积为

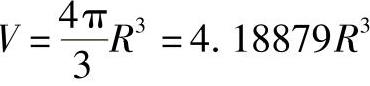
所以当12等分球面时，用圆柱面法展开球面的容积的误差为2.295%。

3.近似展开方法合理性的第三判断标准

（1）微分几何弧长计算方法 曲线的数学方程有直角坐标方程、极坐标方程和参数方程三种，相应的有三种弧长求解公式，分别如下：

1）由直角坐标方程

y=f（x） （9-48）

得出弧长

式中，。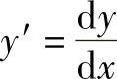

2）由极坐标方程

ρ=ρ（φ） （9-50）

得出弧长

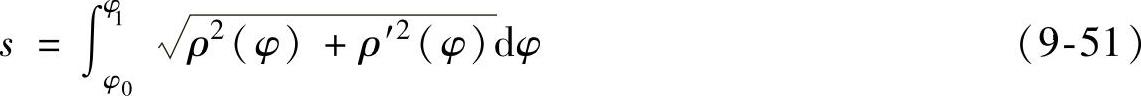
式中，。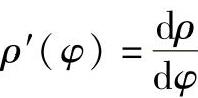

3）由参数方程

得出弧长

式中，。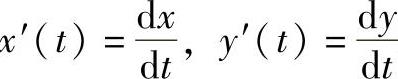

（2）球形容器圆柱近似展开拼缝计算 拼缝的数学方程为

求得弧长

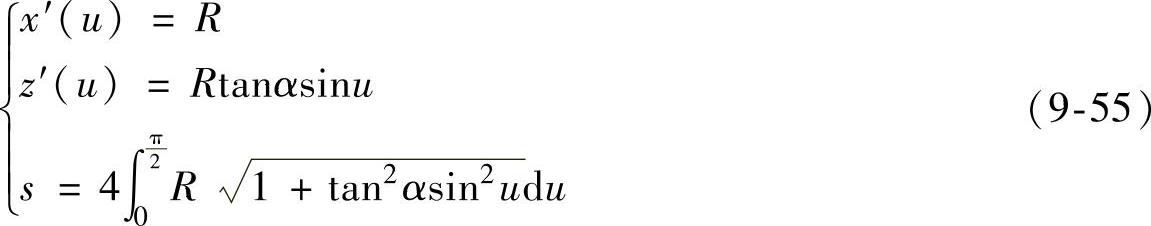
选用数值积分方程

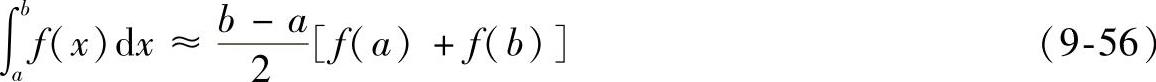
而

代入式（9-56），有

s=12.4233πR

而理论的拼缝为

s=12πR

所以球形容器圆柱近似展开拼缝误差为3.5276%。