实用索多边形作图方法

如图8-34所示，索多边形法的作图方法可按下列步骤进行：

1）正确画出F₁、F₂、F₃的作用线在物体上的位置，这样的图称为位置图，如图8-34a所示。注意：在画位置图时各力作用线之间的已知距离，应选取适当的比例尺画出；各已知角度也应正确定出。

图8-34 索多边形作图方法

2）将各力进行编号，即F₁、F₂、F₃分别用①、②、③表示。(www.xing528.com)

3）选用适当的比例尺，在位置图附近任取一点a开始作已知力的力多边形abcd，如图8-34b所示，此图正确地表明了各力的大小和方向，称为力图。如所作的力多边形不封闭，则表示此力系的主矢R′≠0，力系合成的结果为一合力R。力多边形的封闭边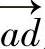所在的位置，不是合力R作用线的位置。为此，应继续作图求出合力R作用线的位置。

4）在力多边形的附近任选一点O，称为极点。由极点向力多边形各顶点作连线，则线段Oa、Ob、Oc、Od称为射线。由极点向力多边形的第一个顶点与最后一个顶点所作的两条射线Oa、Od，命名为α、ω，其余的射线则以与它相交的两个矢量所对应的力的编号来命名。例如，射线Ob与矢量F₁、F₂相交，矢量F₁、F₂所对应的力的编号为①、②，所以射线Ob命名为1-2；同理，Oc命名为2-3。

5）在位置图上力F₁的附近任取一点E，过E点作一直线α平行于射线α与力F₁的作用线相交于A点；过A点作直线1-2平行于射线1-2与力F₂的作用线相交于B点；过B点作线2-3平行于射线2-3与力F₃的作用线相交于C点；再过C点作一直线ω（即CF）平行于射线ω。直线α、1-2、2-3、ω等称为索线，由这些索线所组成的多边形EABCF称为索多边形（见图8-34a）。

6）延长索线α与ω得交点K，则合力R的作用线必通过K点。过K点作平行于力多边形上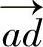（R）的直线，就得到力R的作用线。