通过力的平移可使空间任意力系由汇交力系和力偶系两部分组成。因此,其图解过程包含图解汇交力系和图解力偶系两个部分。下面同样以一实例对图解空间任意力系展开讨论。
例8-6 如图8-19所示,三根绳索缚于支座的B、C、D点上。将绳索的力用点A的等效力偶系代替。
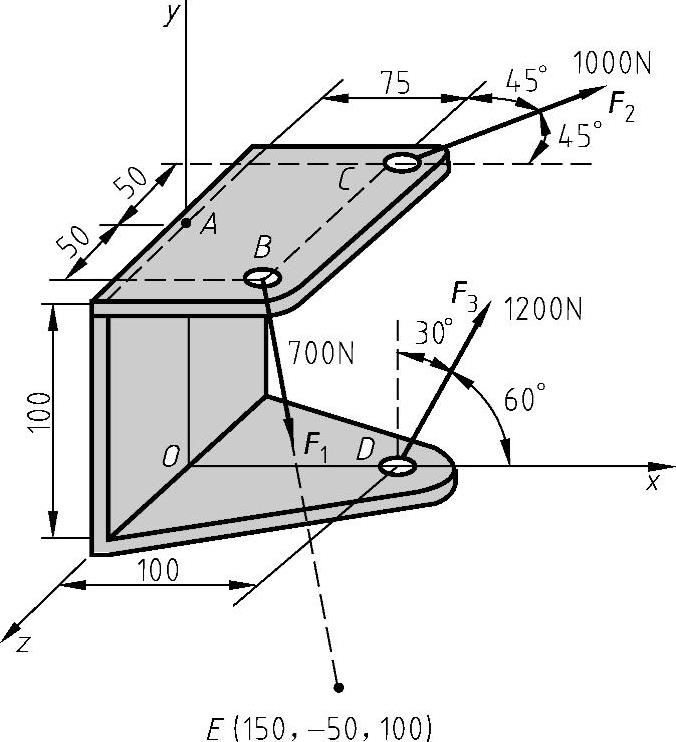
图8-19 支座受力直观图
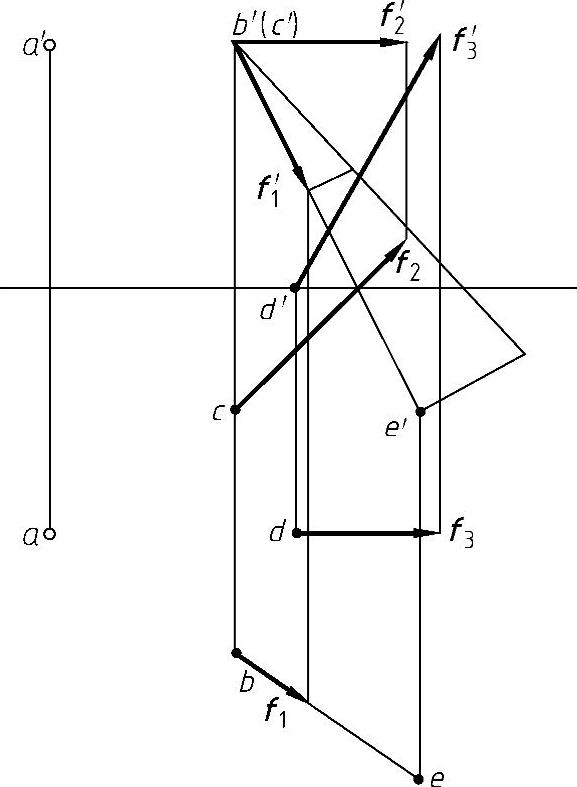
图8-20 支座受力投影图
1.图示
如图8-20所示,根据支座受力的直观图上的尺寸绘制出A、B、C、D四个点的投影,并以1∶10的比例画出过B、C、D三个点的绳索拉力F1、F2、F3的投影。其中,F2处于水平位置,其水平投影反映该力的实际大小,F3处于正平位置,其正面投影反映该力的实际大小,而F1处于一般位置,因此用构造直角三角形求实长的方法先求出BE线实长,将F1度量到实长线上,再确定F1的投影。
2.图解
(1)汇交力系部分的图解步骤 如图8-21所示。
1)将F1、F2、F3三个力的起始点B、C、D平移到A点,三个力也随之一起平移,应用Au- toCAD的捕捉功能可以精确地实现这一平移。
2)用平行四边形法则将F2、F3合成为F23,再将F23与F1合成为F。
3)用尺寸标注功能,设定好精度要求,标注出F的大小,根据作图比例可知合力大小为174.16N×10=1741.6N。
(2)力偶系部分的图解步骤 如图8-22所示。
1)求A点到F1、F2、F3各力作用线的距离。其中,F2的作用线为水平线,在水平投影面上过a作f2的垂线即可得到A点到F2之间的距离,图中用对齐方式直接标注出尺寸17.68mm,省略了作垂线的过程。同理,F3的作用线为正平线,在正投影面上过a′作f3′的垂线即可得到A点到F3之间的距离,图中用对齐方式直接标注出尺寸136.6mm,也省略了作垂线的过程。而F1的作用线是一般位置直线,图中用旋转法将其旋转成正平线,A点也随之旋转,然后在正投影面上标出尺寸77.26mm,即为A点到F1作用线的距离。
2)求各附加力偶的大小。将各力的大小乘以其平移到A点的距离即可得到各附加力偶的力矩大小。具体为
M1=F1×77.26mm/1000=54.028N·m
M2=F2×17.68mm/1000=17.68N·m
M3=F3×136.6mm/1000=163.92N·m
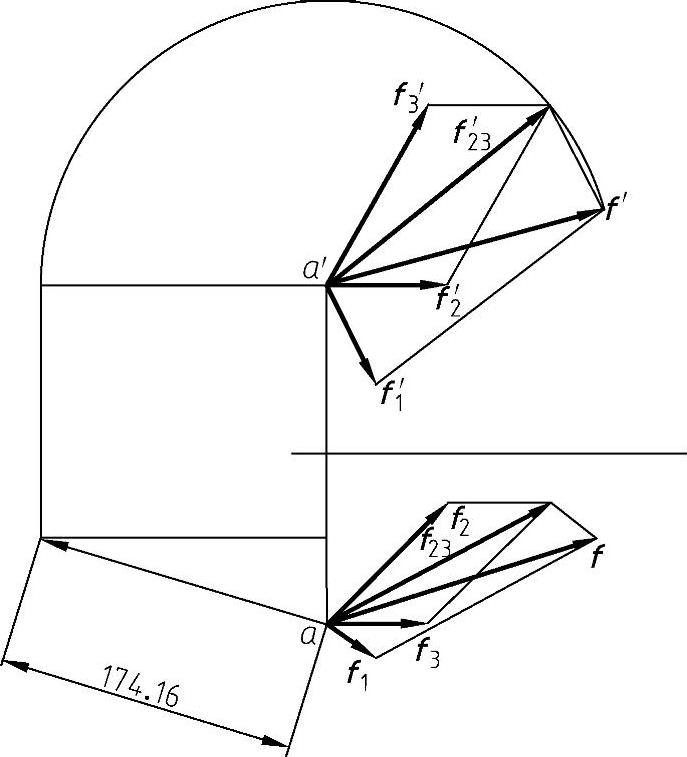
图8-21 汇交力系图解
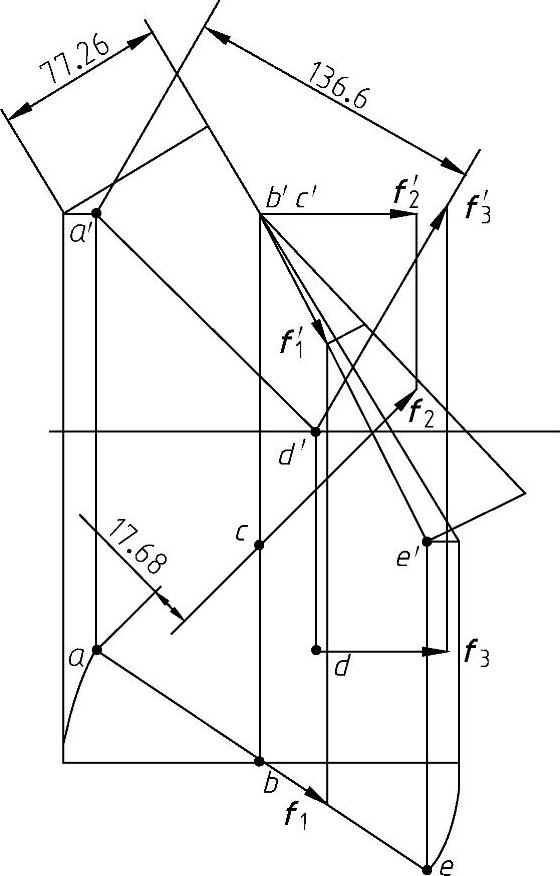
图8-22 力偶系图解
例8-7 如图8-23所示,在点A和B受到支承的矩形板,同时用一根绳索CD拉着。已知绳索的张力为200N,确定绳索作用于C的力对点A的力矩。
要求绳索作用于C的力对点A的力矩,关键是要求出A点到力作用线的距离L,有了距离L,只需将力乘以距离就可以得到力矩。因此图解的步骤如下:
1)如图8-24所示,根据图中所注尺寸确定A、B、C、D四个点的投影,以及CD线的投影(画图比例为1∶10)。
2)用换面法将力作用线CD变换为铅垂线,A点也随之一起变换。
3)在新投影面上标注A点到CA线的距离为20.6397mm。
4)计算已知力与距离的乘积得到力矩为
M=(20.6397×10×200/1000)N·m=41.2794N·m
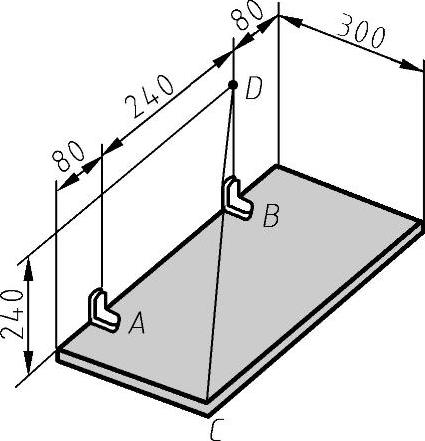
图8-23 例8-7的图形条件
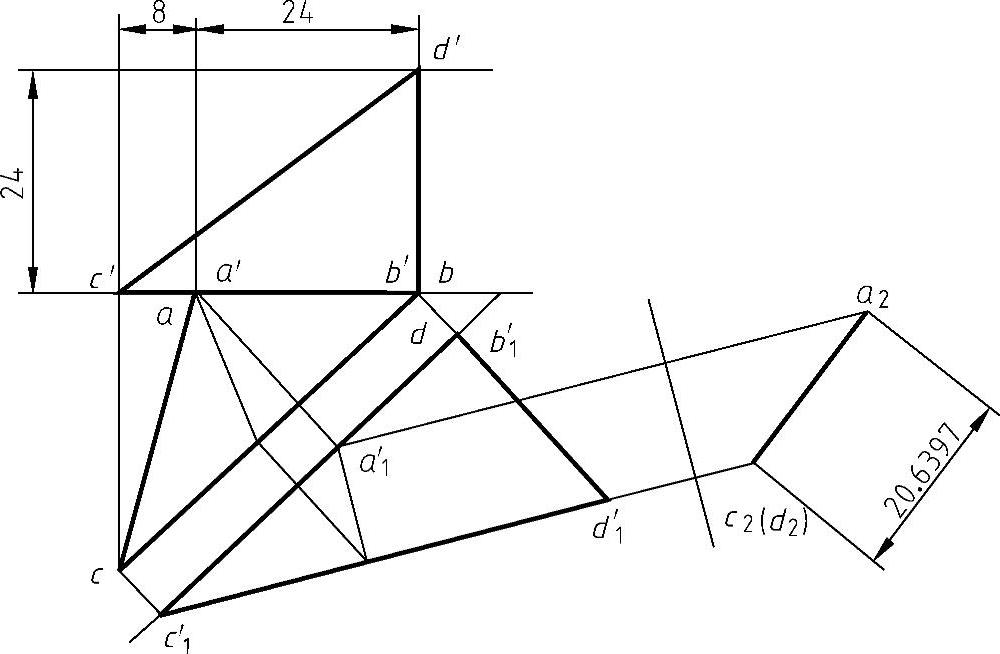
图8-24 力矩的图解
例8-8 如图8-25所示,一个半径r=240mm、质量为30kg的均质管道顶盖,通过绳索CD保持水平位置。假设位于点B的支承不提供任何径向推力,计算绳索的张力和点A、点B的约束力。
解 画出受力投影图,如图8-26a所示。依次图解绳索的张力,以及A点、B点的约束力。
(1)图解绳索张力 因为A、B两点的约束力所在的AB杆为侧垂线,其侧面投影积聚为一个点a″(b″),所以A、B两点的约束力的侧面投影也过a″(b)″,将各力的侧面投影当作一个平面任意力系,各力的投影对a″(b)″取矩,其中t″对a″(b)″的矩的力臂长可在图8-26b中直接量取,f″对a″(b)″的矩的力臂长为已知,而其余力的侧面投影均过a″(b)″,不产生矩,因此有240×f″=214.66×t″,f″=30×9.81N=294N,由此解出t″=328.71N。在侧投影面上利用直角三角形法求出绳索张力T的实长,再从t″的端点引线与所作三角形的另一直角边的平行线,该线与实长线相交,即可量取T的实际大小为T=343N,如图8-26b所示。
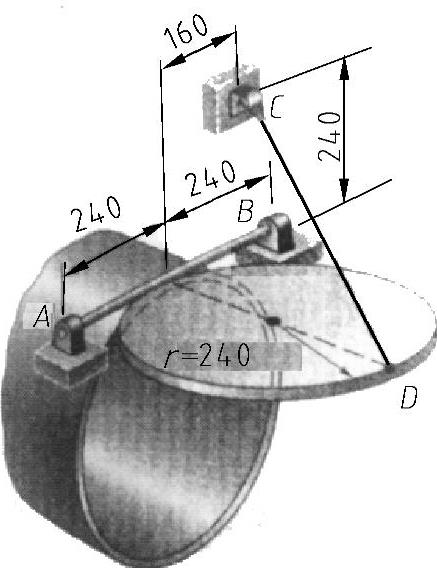
图8-25 例8-8的图形条件
(2)图解A、B两点的约束力 画出正面投影图,如图8-26c所示,将各力的正面投影当作一个平面任意力系,各力的投影对a′取矩,其中t′对a′的矩的力臂长可在图8-26c中直接量取,f′、bz′对a′的矩的力臂长为已知,而其余力的正面投影均过a′,不产生矩,因此有t′×199.8-f′×240+b′×480=0,由此解出b′z=73.5N。由图8-26c可知a′x=98N,a′z=f′-b′z-146.81N=73.5N。
画出水平投影图,如图8-26d所示,将各力的水平投影当作一个平面任意力系,各力的投影对a取矩,其中t对a的矩的力臂长可在图8-26d中直接量取,t的长由直角三角形法求出,为已知,因此有t×379.47-by×480=0,由此解出by=245N。由图8-26b可知ay+by=294N,由此可得ay=294N-by=49N。根据所求得的A、B各点处的约束力的分量可求出该两点处的约束力的大小和方向,如图8-26e所示,有NA=131.94N,NB=255.79N。
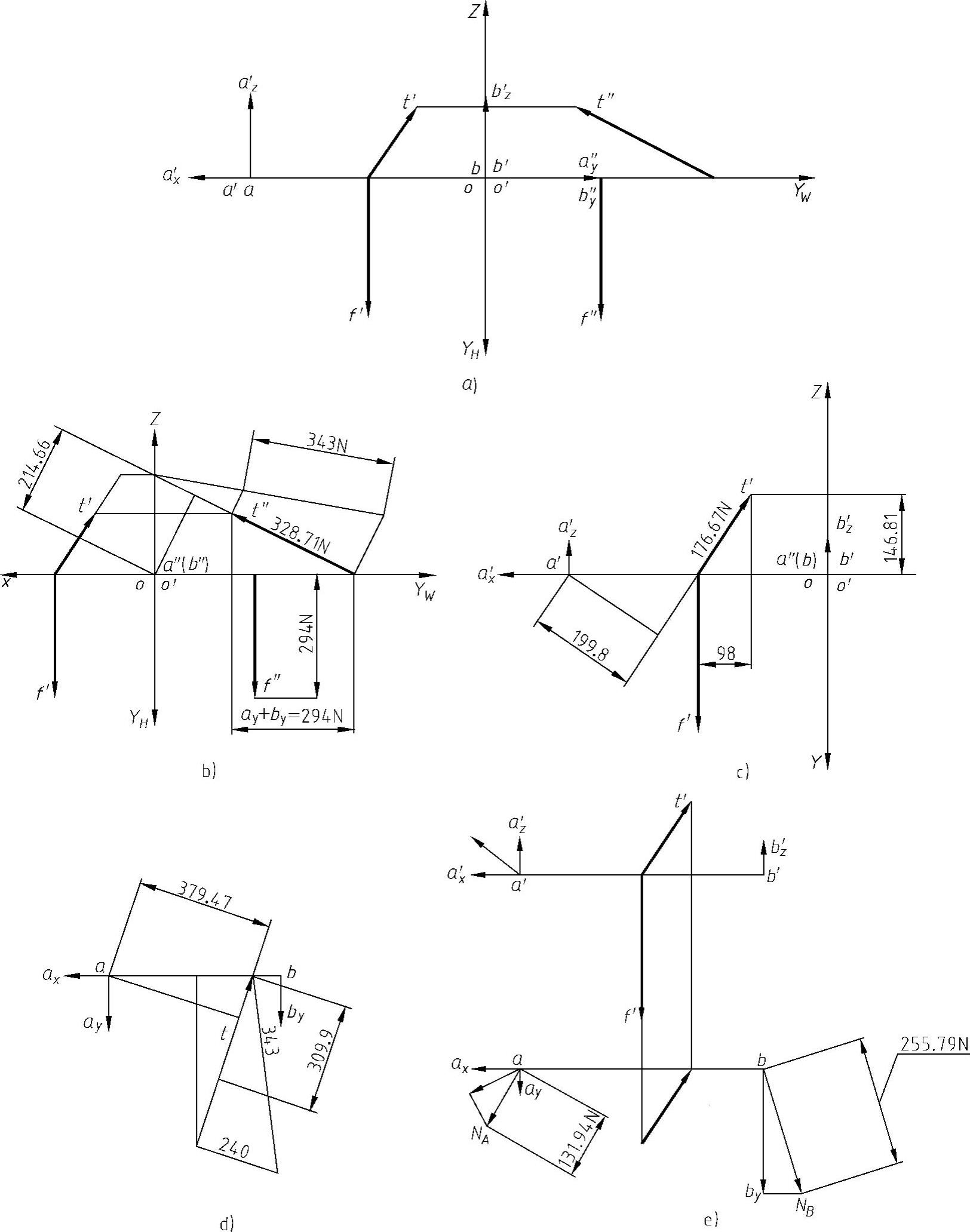
图8-26 例8-8图解
例8-9 弯成图8-27所示形状的一段刚性管子ABCD,在转角C处悬挂质量为200kg的载荷。管子由点A和点D处的球形铰链支承,球形铰链分别紧固在地板和垂直墙面上,管子还用连接管子BC段中点E和墙上一点G的绳索拉着。试图解使绳索内张力最小的点G的位置及对应张力的最小值。
1)根据图8-27所示的尺寸,画出AB、BC、CD各杆及E点和重力W的投影图,如图8-28a所示,画图比例为1∶10。
2)将A、D连线作为一条轴线,以便图解重力W、拉力T对此轴线的矩。而A、D两点的约束力因过此轴而不产生对此轴的矩。
3)二次投影变换将AD轴线变换为投影面的垂直线(铅垂线)重力W和点E也随之变换,并在图中标注出重力W的投影长为w2=146.24N,E点的投影e2,AD线积聚性投影a2d2与e2之间的距离200mm及a2d2到w2(重力W的投影)的距离178.89mm,如图8-28b所示。
4)在H2投影面上应有关系t2×200mm=146.24N×178.89mm,由此求出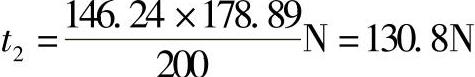 根据作图比例1∶10,可得T=130.8N×10=1308N。其方向如图8-28c所示。
根据作图比例1∶10,可得T=130.8N×10=1308N。其方向如图8-28c所示。
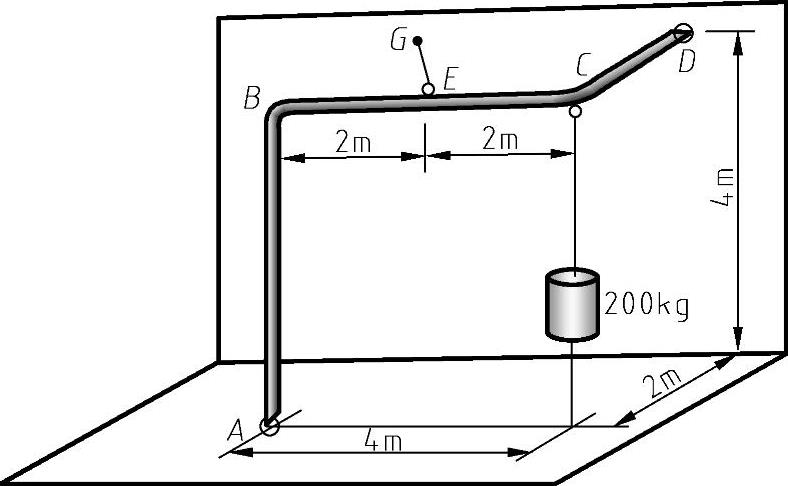
图8-27 例8-9图
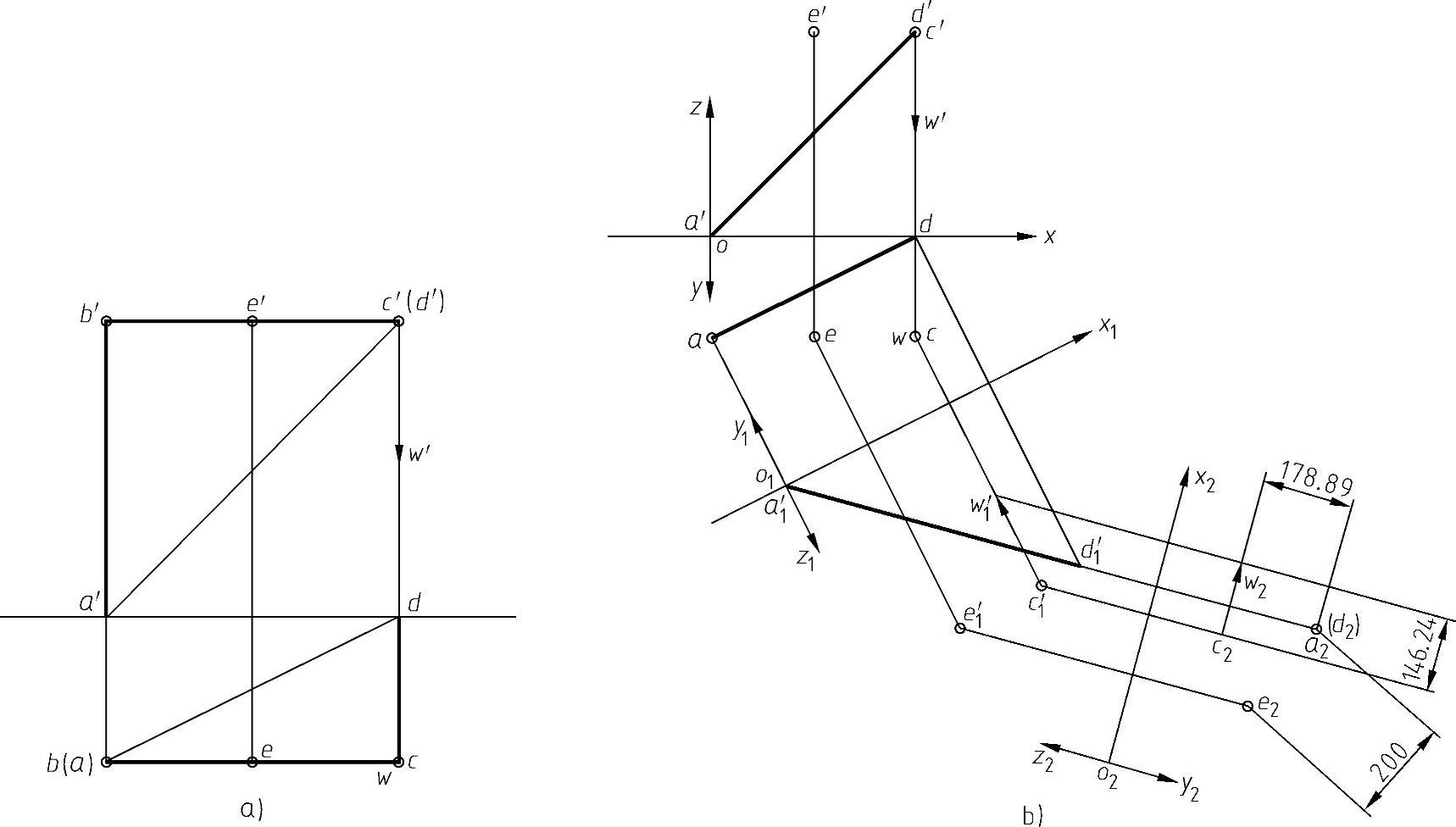
图8-28 图解过程(注:为使图形简捷起见,图中未标注的投影轴的符号参见图8-28b)
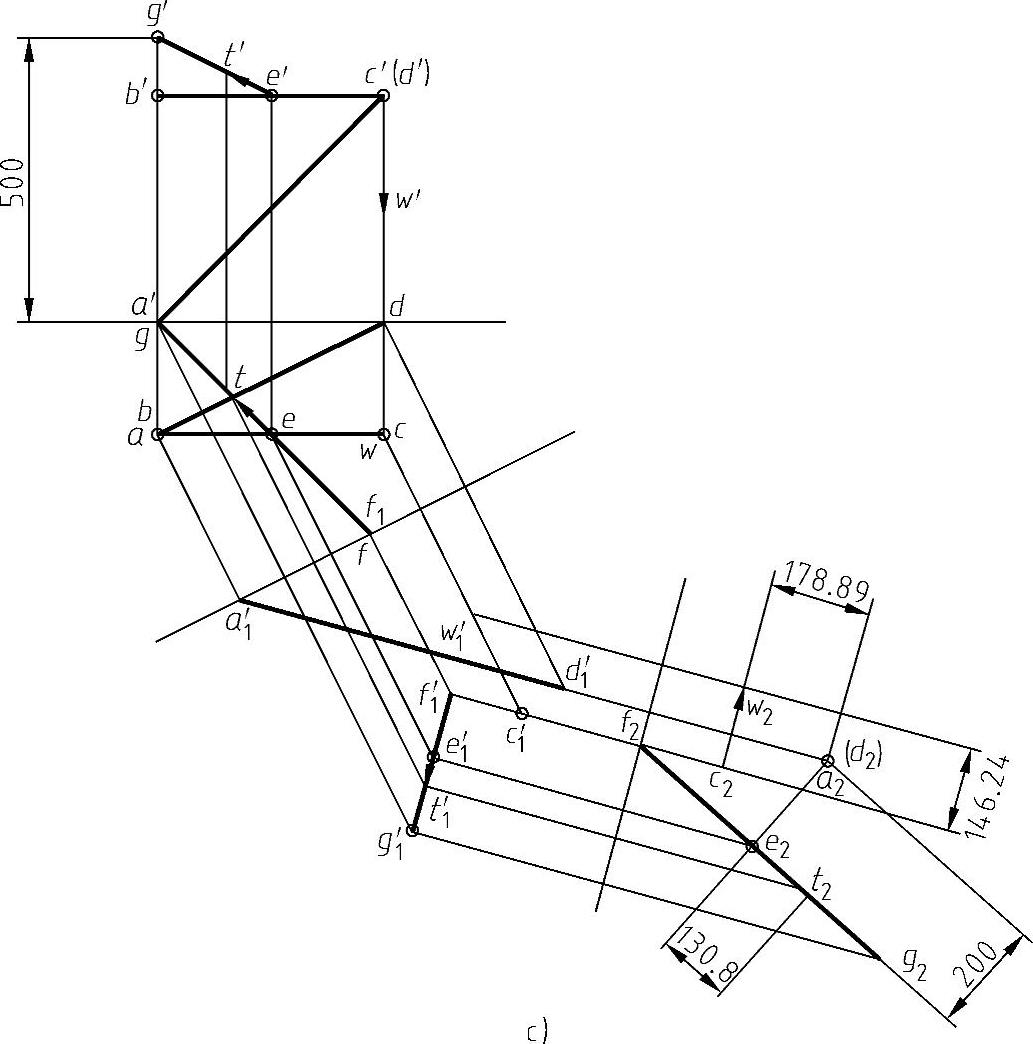
图8-28 图解过程(注:为使图形简捷起见,图中未标注的投影轴的符号参见图8-28b)(续)
5)图解G点位置。因G点在V面上,在H2投影面上,延长e2t2与x2轴交于f2点,由f2点求出F点在V1面上的投影f1′,f1′应为过f2点垂直于x2轴的投影联系线与过e1′点的x2轴平行线的交点(在V1/H2体系中,因为在H2投影面上e2f2⊥e2a2,根据直角投影定理,应有e1′f1′//x2轴),由f1′引线垂直于x1轴得到f1、(f),将f、e两点用直线相连并延长与x轴交于g,由g在V1面上求得g1′,根据V面与V1面z坐标相等的关系可求出g′。由此可量取G点的x、y、z坐标为x=0,y=0,z=5m。
上面所选用的实例具有代表性,用AutoCAD作为工具,作图精确性好,直接将力的大小标注在图上比较直观显见。另外,图解过程也有助于图解训练和实现画法几何的应用价值。为了充分体现图解法的优越性,下面列出例8-5~例8-9的矢量法求解过程,以便更加理解基于Auto-CAD的图解工程静力学问题是一种值得推广的实用方法。
例8-5的矢量法求解过程如下:
图8-29所示为例8-5中所描述的箱子的受力图,以A点为研究对象,有四个力的作用,其中有三个力的大小未知,引入单位矢量i、j、k,将每个力分解为三个分量。
对于重力
G=-mgj=-1597.4j
对于力TAD、TAB和TAC,首先要确定矢量 、
、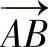 和A
和A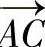 的大小和分量。
的大小和分量。
用λAD表示沿AD方向的单位矢量,有
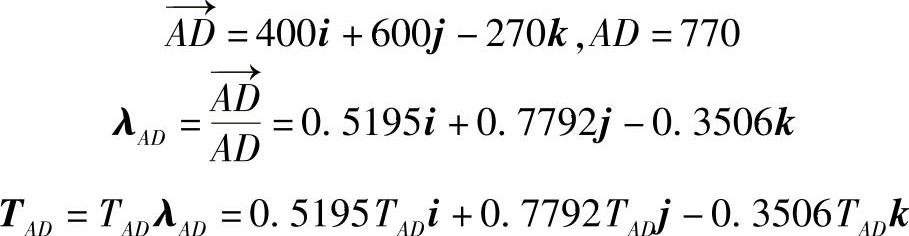
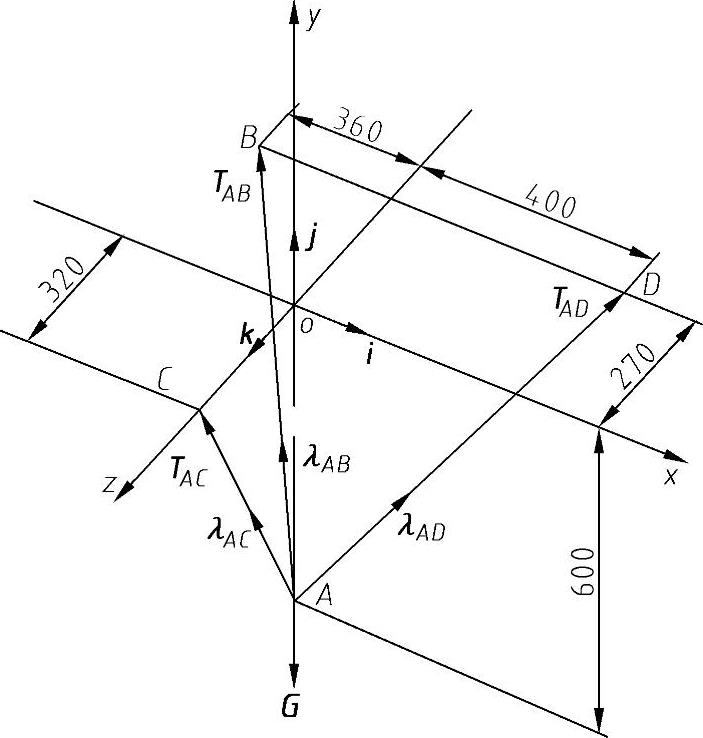
图8-29 受力图
用同样方法得到
TAB=TABλAB=-0.48TABi+0.8TABj-0.36TABk(https://www.xing528.com)
TAC=TACλAC=0.8824TACj+0.4706TACk
平衡条件:由A点平衡,得
∑F=0,TAB+TAD+TAC+G=0
将上式代入并按i、j、k合并同类项得
∑Fx=0,-0.48TAB+0.5195TAD=0
∑Fy=0,0.8TAB+0.7792TAD+0.8824TAC-1597.4=0
∑Fz=0,-0.36TAB+(-0.3506TAD)+0.4706TAC=0
解方程得:TAD=526.672N,TAB=569.991N,TAC=828.482N。
例8-6的矢量法求解过程如下:
首先,计算从点A到各力作用点的相对位置矢量,并将各力分解为直角坐标分量。显然FB=(700N)λAB,其中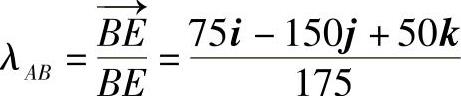 ,采用m和N为单位有
,采用m和N为单位有
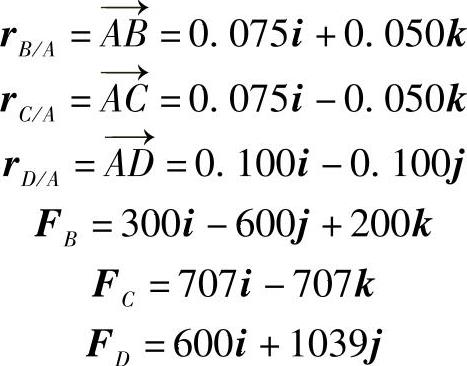
点A的等效力系包括力R=∑F和力偶MAR=∑(r×F)。通过将力R的x、y和z方向的分量相加,得
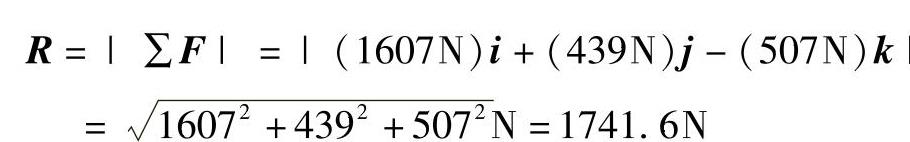
各力偶矩表示形式为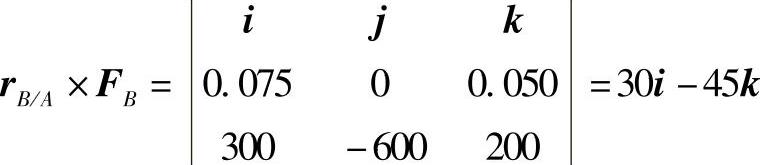 ,力偶矩大小为∑
,力偶矩大小为∑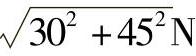 ·m=54.03N·m
·m=54.03N·m
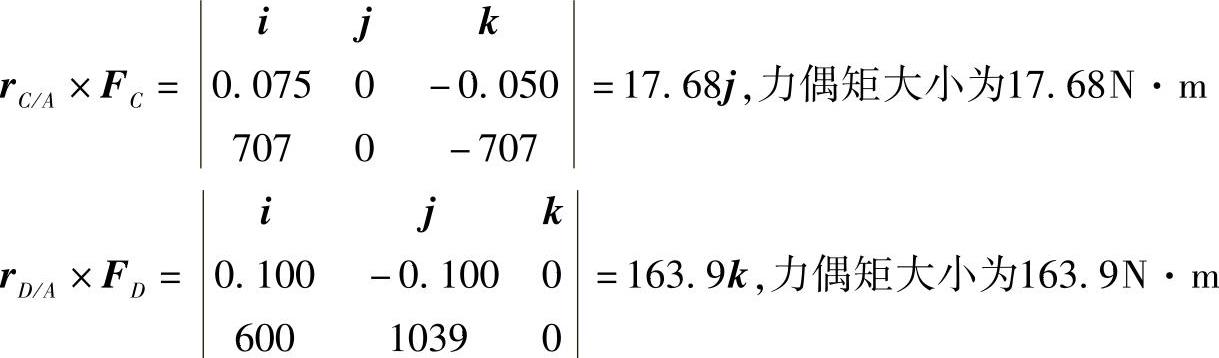
例8-7的矢量法求解过程如下:
作用于点C的力F对点A的矩MA可以通过以下矢量积获得。计算参考图如图8-30所示。
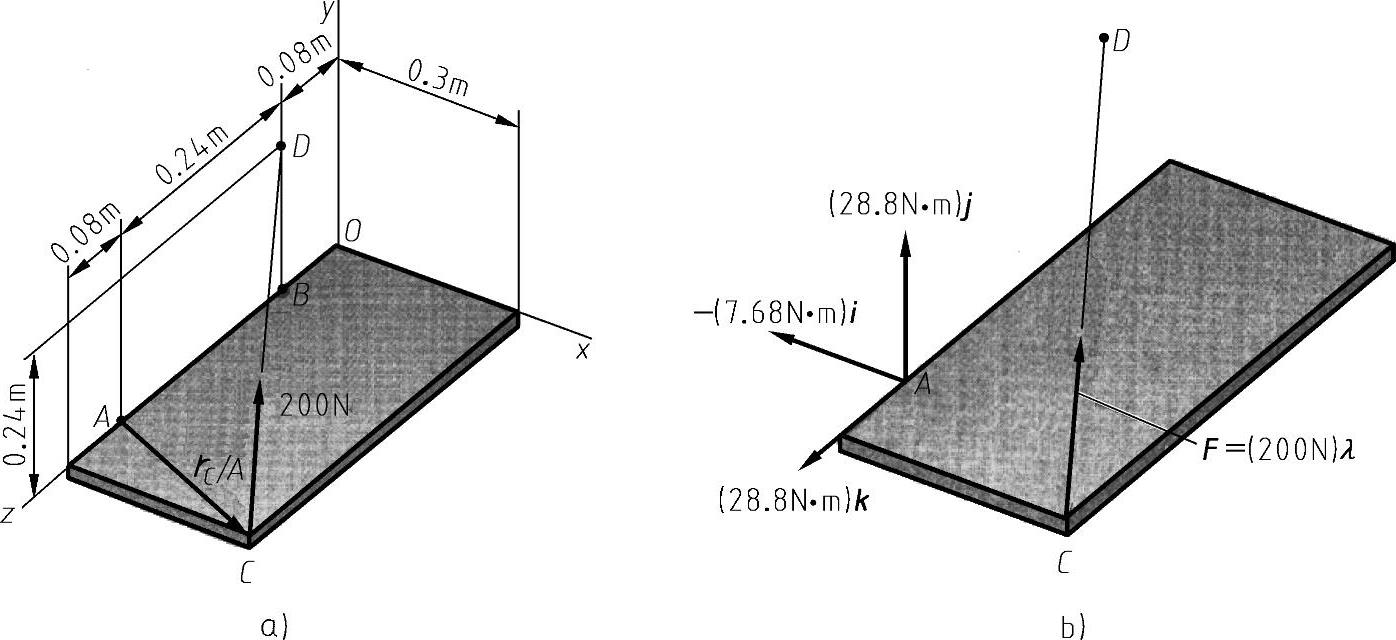
图8-30 例8-7图计算参考图
MA=rC/A×F (1)
其中,rC/A是从点A到点C的矢量,有

F为沿CD方向作用的200N的力,引入单位矢量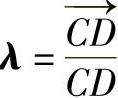 ,可以写为
,可以写为

将矢量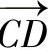 分解为直角坐标分量的形式,有
分解为直角坐标分量的形式,有
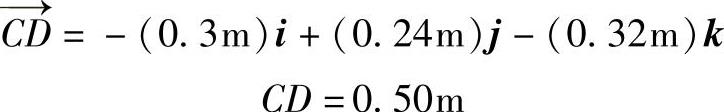
代入式(3),有
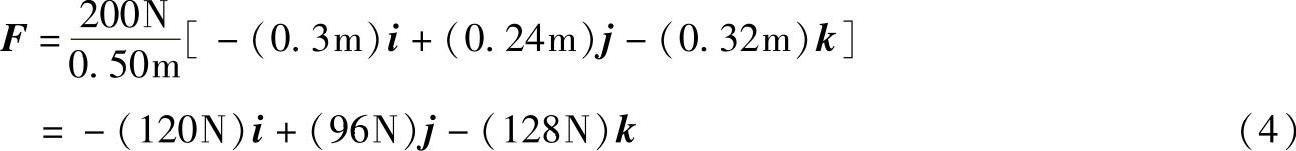
将式(2)和式(4)中的rC/A和F代入式(1)有
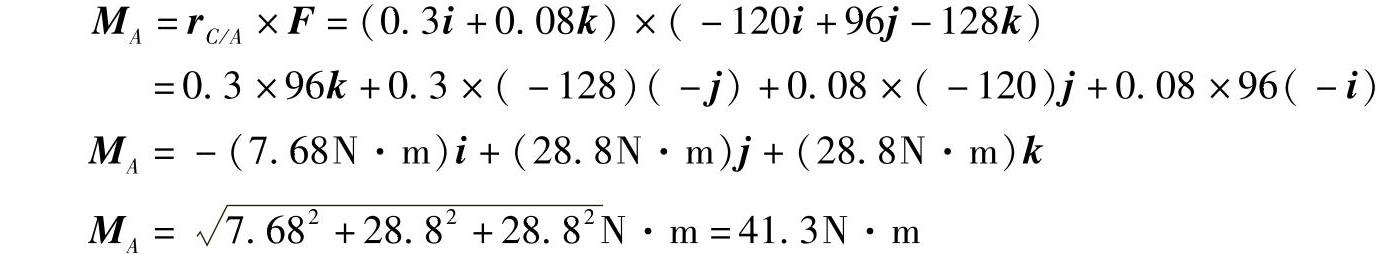
例8-8的矢量法求解过程如下:
有坐标轴的受力图如图8-26所示。作用在隔离体上的力为顶盖的重力。即
W=-mgj=-(30kg)×(9.81m/s2)j=-(294N)j
约束力包括6个未知量,即绳索作用力T的大小、铰接点A处约束力的3个力的分量和铰接点B处的两个力的分量。作用力T表示为直角坐标分量(图8-31),有
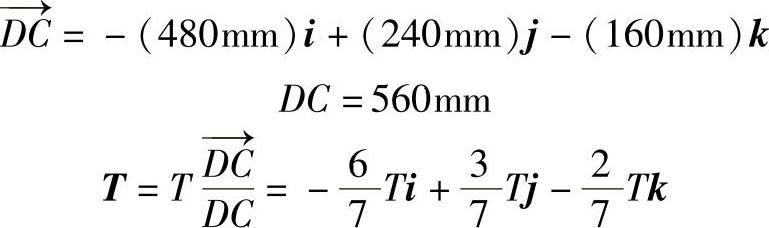
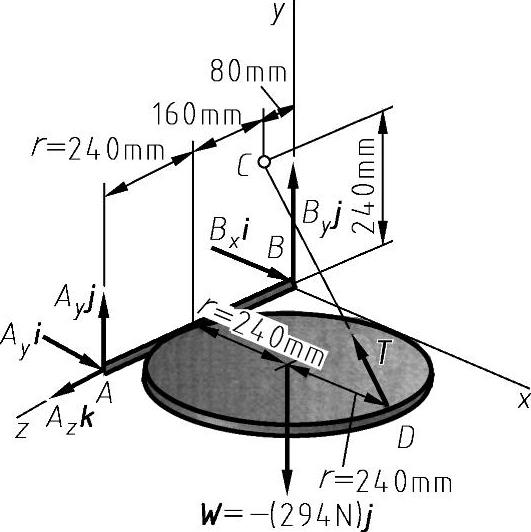
图8-31 例8-8隔离体图
作用在管子顶盖的力等效为零力系,即
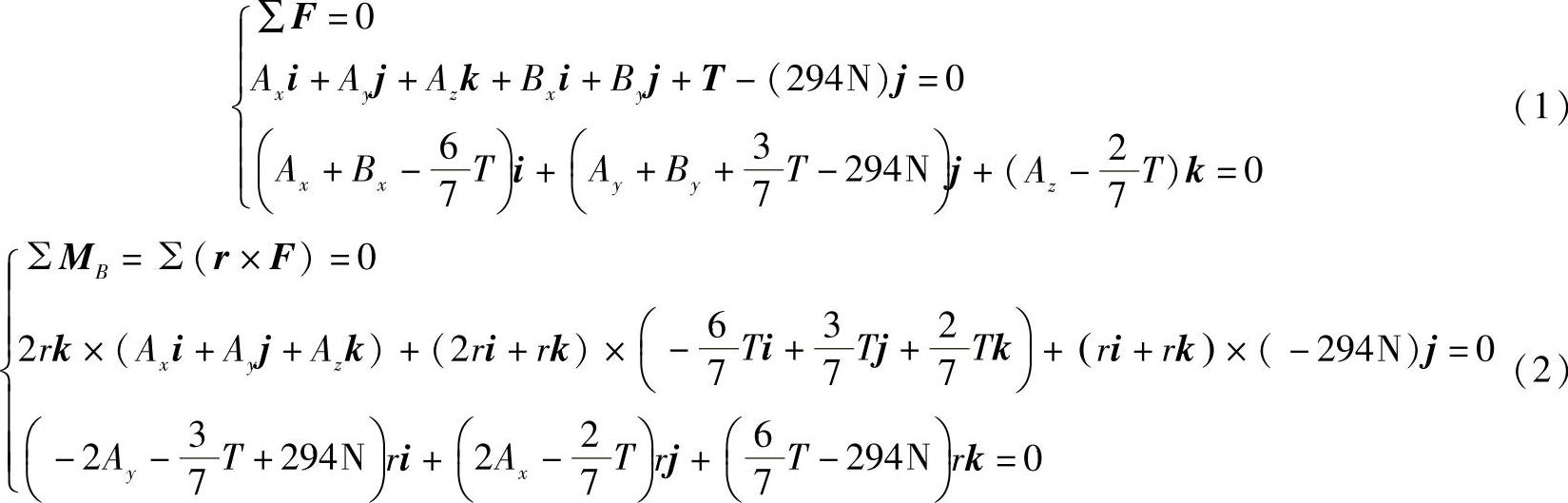
令式(2)中的单位矢量的系数为零,可以写出3个标量方程,从而可以求出
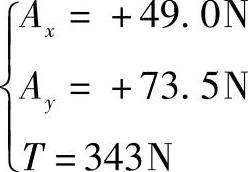
令式(1)中的单位矢量系数为零,可以得到另外3个标量方程。将T、Ax、Ay代入这3个方程,有
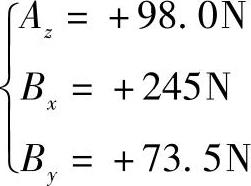
因此点A和点B的约束力为
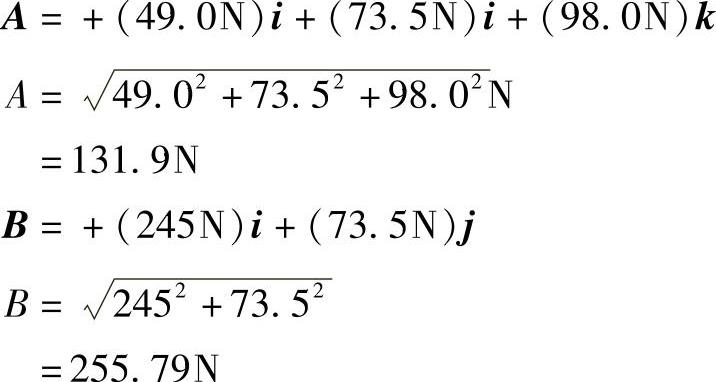
例8-9的矢量求解过程如下:
如图8-32所示,管子的受力图包括载荷W=-(1962N)j,以及点A、点D的约束力和绳索拉力T。为了在计算中排除点A和点D的约束力,对AD求力矩之和。用λ表示沿AD的单位矢量,有
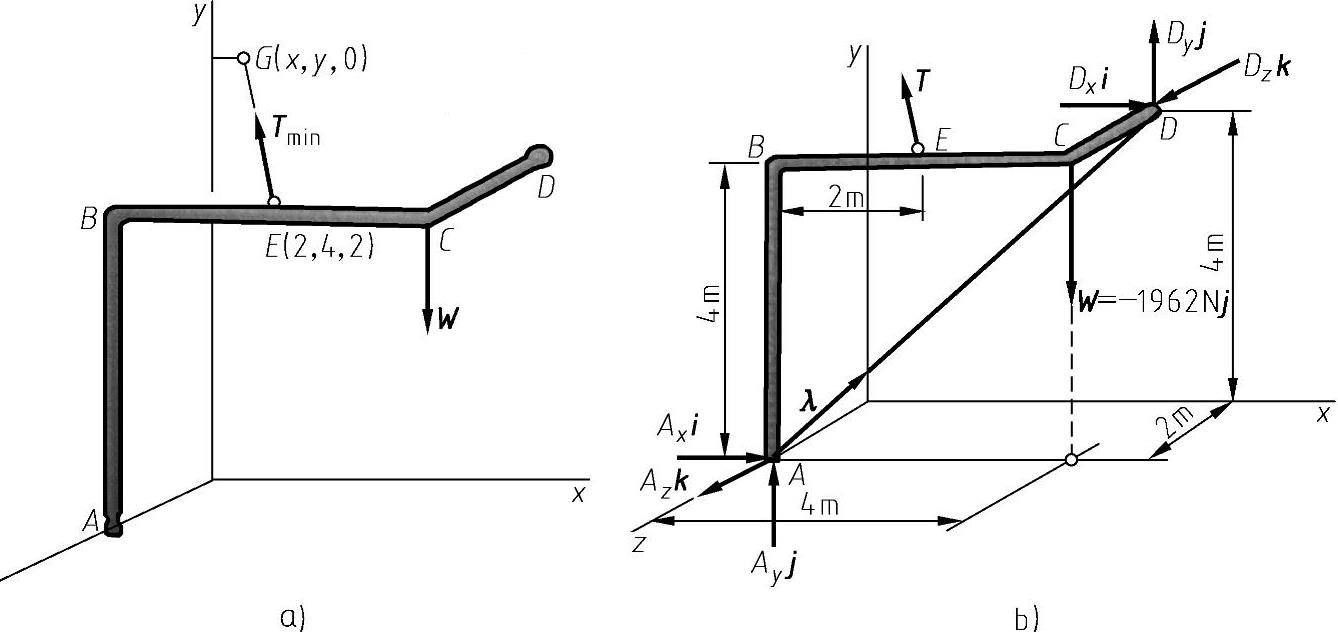
图8-32 受力图
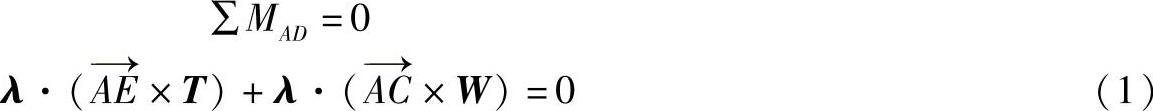
式(1)中的第2项可以进行如下计算
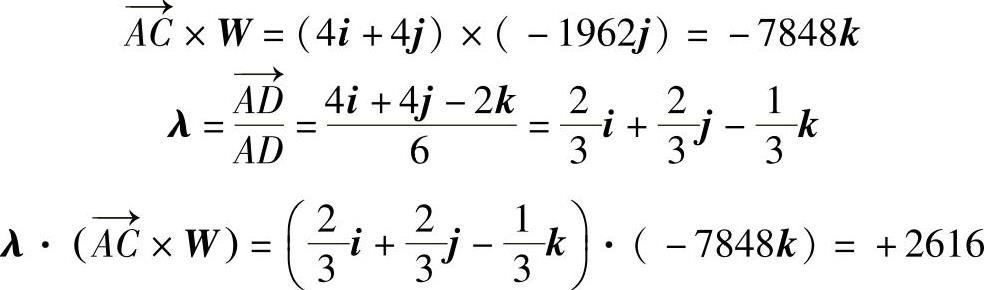
将获得的值代入式(1),有

张力的最小值:利用混合积的交换性,将式(2)重写为

由式(3)可见,T在矢量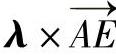 上的投影为常值。当T平行于
上的投影为常值。当T平行于
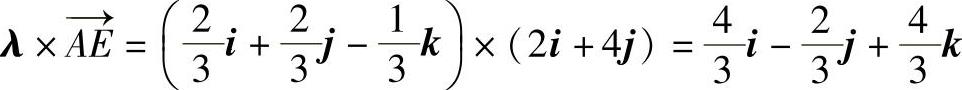
时,T值最小。由于对应单位矢量是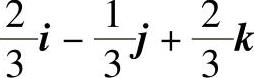 ,故有
,故有

将T和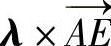 代入式(3),并计算标量积,可以得到2T=-2616N,因此T=-1308N。将此值代入方程(4),有
代入式(3),并计算标量积,可以得到2T=-2616N,因此T=-1308N。将此值代入方程(4),有
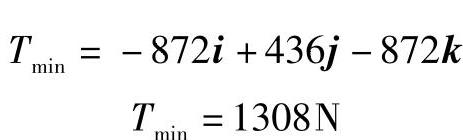
点G的位置:由于矢量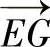 和Tmin方向相同,它们的分量必然成比例。将点G的坐标用x、y和0表示,有
和Tmin方向相同,它们的分量必然成比例。将点G的坐标用x、y和0表示,有
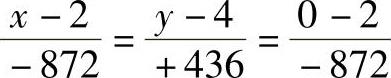
故x=0,y=5m,z=0。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




