图解平面任意力系，简洁高效！

当力系中各力的作用线处于同一平面且可以任意分布时，称其为平面任意力系。可以通过力的平移获得一个平面汇交力系，而为了使得平移后的力系与原力系等效，每平移一个力需要附加一个力偶，因此平面任意力系等效为两个简单力系：平面汇交力系和平面力偶系。其中平面汇交力系的图解方式上面已经介绍过了，而力偶系中的每一个力偶矩的大小和方向由每一个力的大小和该力平移到汇交点的距离决定，这一距离由简单的几何作图就可解决，然后将力的大小乘以平移的距离即可得到力偶矩的大小。

例8-3 如图8-13所示，大小为800N的力作用于托架上，确定该力对B点的力矩。

根据力对点的矩的定义，图解法非常简单、方便，只需根据托架的尺寸确定A、B两点的位置，过A点画出力的作用线，再过B点作力作用线的垂线，用标注尺寸的方法量取垂线距离，将此距离乘以力的大小即为所求的力矩。具体作图如图8-14所示。

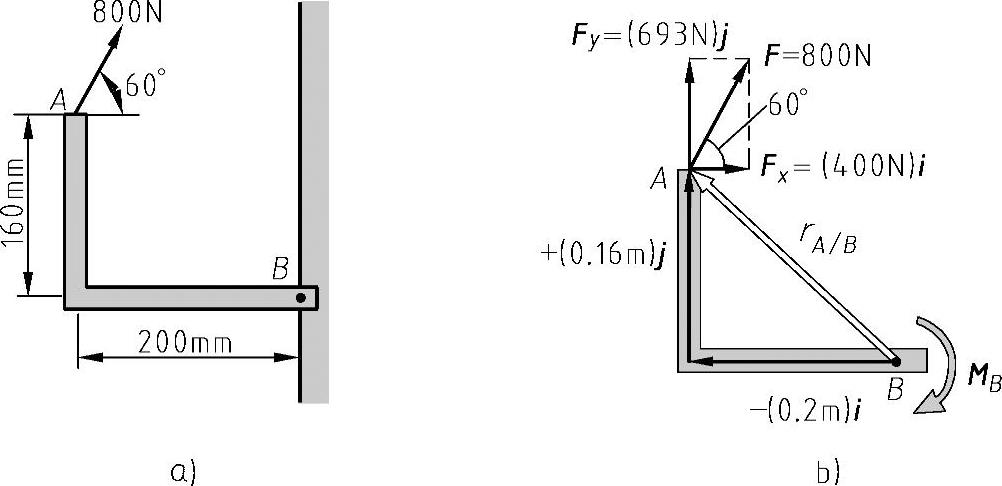
图8-13 例8-3的图形条件

a）托架整体情况 b）托架受力图

图8-14 力矩的力臂长度图解

根据图解的力臂长度和已知力可以算出力矩的大小为

M_B=800×253.2051N·m=202.56N·m

例8-4 起重机自重P₁=10kN，可以绕铅直轴AB转动；起重机的挂钩上挂一自重为P₂=40kN的重物，如图8-15所示。起重机的重心C到转动轴的距离为1.5m，其他尺寸如图8-15所示。求推力轴承A和B处的约束力。

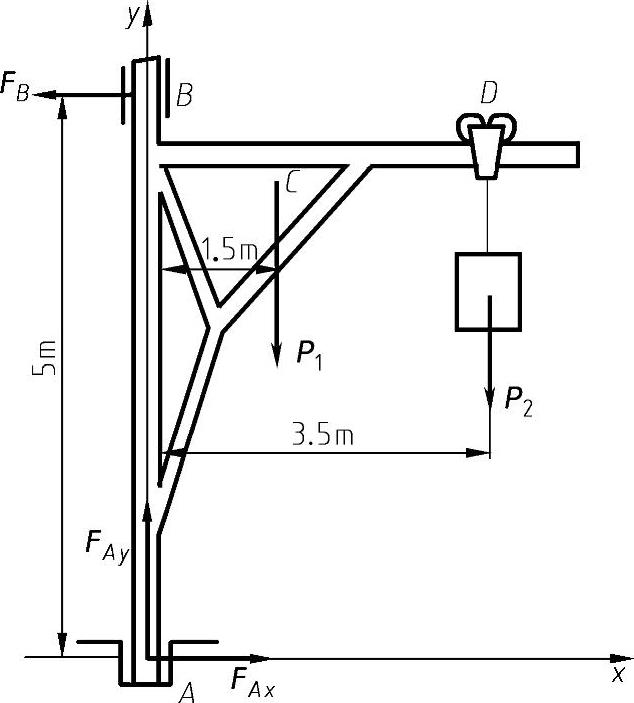
图8-15 例8-4的图形条件

图解 1）画出受力图。

2）标注尺寸。

3）将P₁、P₂、F_B三力平移至A点，构成一平面汇交力系，如图8-16a所示，由图可知

图8-16 构造的平面汇交力系

F_Ay=P₁+P₂=10kN+40kN=50kN

各力平移到A点后，为使与原力系等效，要附加P₁、P₂、F_B三个力平移产生的力偶，由图8-16b可知，三个力偶矩的大小分别为

M₁=P₁×1.5m=15kN·m，M₂=P₂×3.5m=140kN·m，M₃=F_B×5m=5F_Bm其中，P₁、P₂对A点产生负值力矩，F_B对A点产生正值力矩，因此有(www.xing528.com)

5F_Bm=（15+140）kN·m=155kN·m

故F_B=31kN，而F_Ax与F_B大小相等、方向相反。

对上述平面任意力系的两个例子，也可用解析法加以求解，一方面可验证图解法的正确性，另一方面可通过比较两种方法的求解过程，理解图解法直观和简捷性的优点。

例8-3的解析解：力F对B点的力矩M_B可以通过矢量积得到，即M_B=r_A/B×F，其中r_A/B为从B到A的矢量，将r_A/B和F分解为直角坐标分量的形式有

r_A/B=-（0.2m）i+（0.16m）j

F=（800N）cos60°i+（800N）sin60°j=（400N）i+（693N）j

由单位矢量的矢量积关系，有

M_B=r_A/B×F

=[-（0.2m）i+（0.16m）j]×[（400N）i+（693N）j]

=-（138.6N·m）k-（64.0N·m）k

=-（202.6N·m）k

M_B为垂直于图中平面的矢量，方向指向纸内。

例8-4的解析解：以起重机为研究对象，它所受的主动力有P₁和P₂。由于对称性，约束力和主动力都位于同一平面内。推力轴承A处有两个约束力F_Ax和F_Ay，推力轴承B处只有一个与转轴垂直的约束力F_B，约束方向如图8-16b所示。取坐标系如图8-15所示，有

∑F_x=0，F_Ax-F_B=0

∑F_y=0，F_Ay-P₁-P₂=0

∑M_A（F）=0，-F_B×5m-P₁×1.5m-P₂×3.5m=0

求解以上方程，得

F_Ay=P₁+P₂=50kN

F_B=0.3P₁-0.7P₂=31kN

F_Ax=F_B=31kN