计算机实验工程图形学：力的合成与平行四边形法则

力学中各分力可用平行四边形法则求合力，该方法适合于各力共面或者异面两种情况。当各力共面时，直接在此面上用平行四边形法则求其合力，这个法则可以通过实验验证，但无法在数学上证明。可以证明，相交两个力的同面投影用平行四边形法则合成后的结果等于合力在该投影面上的投影。

证明：如图8-3a所示，设相交两个力F₁、F₂的作用线AB、AC构成一个平面，将该平面处

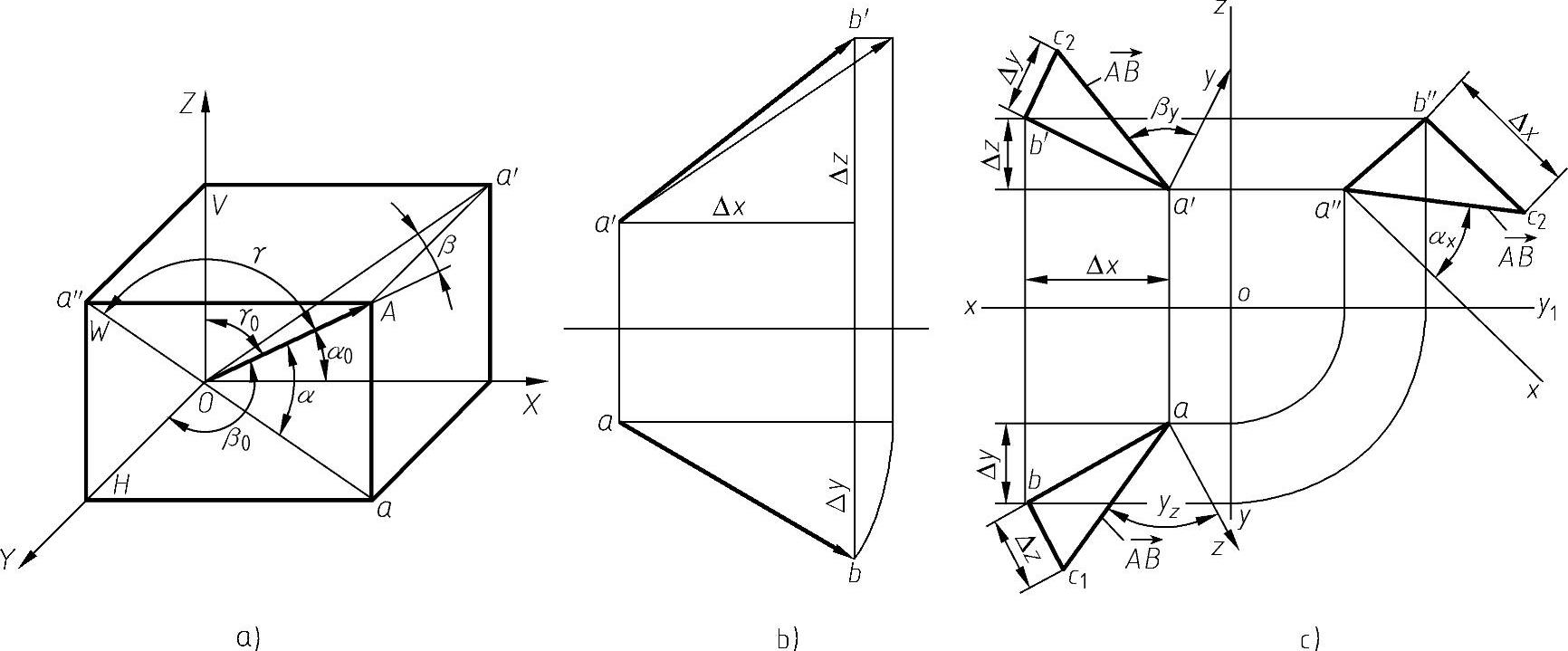
图8-2 力的实长及其与投影面及轴的夹角

a）力与投影面及轴的夹角 b）旋转法求力的实长 c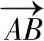）与投影面、投影轴的夹角

于正平面位置（如两个力作用线处于一般位置平面上时，可用换面法将其变换为投影面的平行面），在正立投影面上有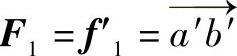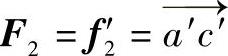：，，在V、H两投影面上分别采用平行四边形法则，在V投影面上，f₁′、f₂′合成为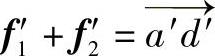；在H投影面上，如图8-3b所示，f₁、f₂合成为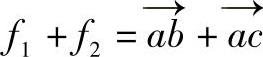，由平行四边形法则知在空间AC//BD，根据正投影原理应有a′c′//b′d′，ac//bd，且a′c′=b′d′，ac=bd，所以ab+ac=ab+bd=ad，因为ad//x轴，且AD为正平线，则有a′d′=AD，a′d′是F₁、F₂两个力在V投影面上投影的合成，等于F₁、F₂两个力的合力在V投影面上的投影，证明完毕。

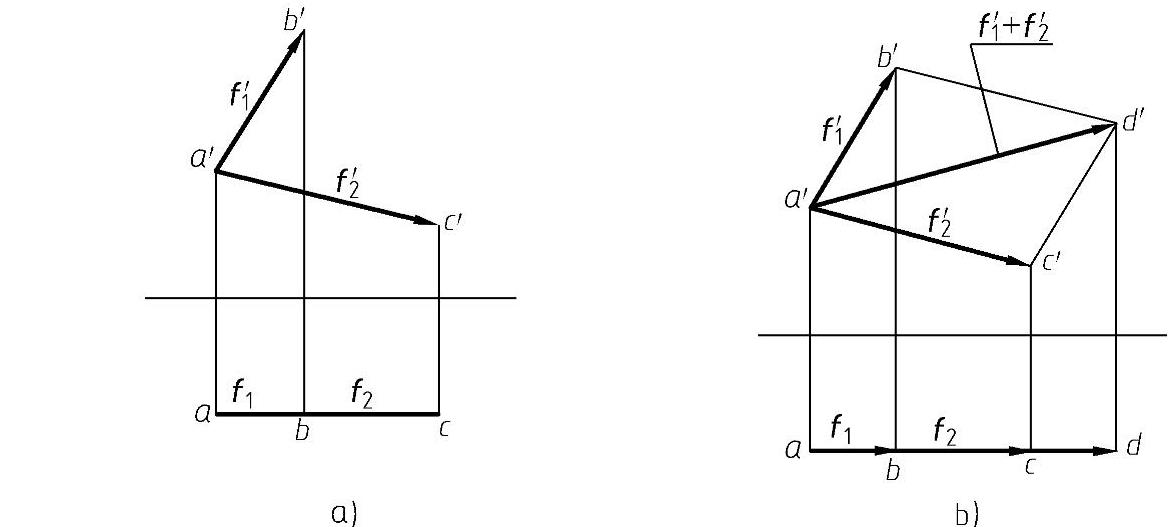
图8-3 力的合成

a）F₁、F₂的作用线AB、AC b）F₁、F₂的合成(www.xing528.com)

推论1 对力作用线为空间交叉的两个力，可以通过平移使其成为相交的两个力，另附加一个力偶与原力系等效，对平移后的相交两力的合成，上述定理仍然有效。

推论2 对n个空间相交的汇交力系的合成，可以用平行四边形法则，将力系中的F₁、F₂两个力合成为一个力R₁，再将F₃与R₁合成为一个力R₂，这样继续合成下去，最后也可以求出力系合成的结果，在此过程中每两个力的合成，上述定理仍然有效。

推论3 对n个空间相交的任意力系的合成，可将各力平移，使其成为一个汇交力系，为与原力系等效，每平移一个力附加一个力偶，最终获得一个汇交力系和一个力偶系，对汇交力系的合成推论2仍有效。

因此，求各力的合力可用平行四边形法则先将各力的同面投影按此法则合成，然后根据合成后的合力的投影求出合力的大小，如图8-4a、b所示。根据力学原理，空间共点各力的合力的大小等于力多边形的封闭边的大小。所谓力多边形就是各力依次首尾相接，最后由初始力的始端向最末力的终端相接构成的封闭多边形。封闭多边形的封闭边即为合力。当然对空间汇交力系来说，力多边形也是空间的多边形，如图8-4c所示。可以证明，在投影图中，将空间各力的同面投影依次首尾相接构成力投影的多边形等于空间力多边形在该投影面上的投影，上面已经证明将各力的同面投影用平行四边形法则合成后的结果等于合力在该投影面上的投影，由图8-4可知，用力多边形方法合成三力的结果与用平行四边形法则将三力合成的结果相等，因此可先由各力的投影作出力多边形的投影，再求合力的大小。

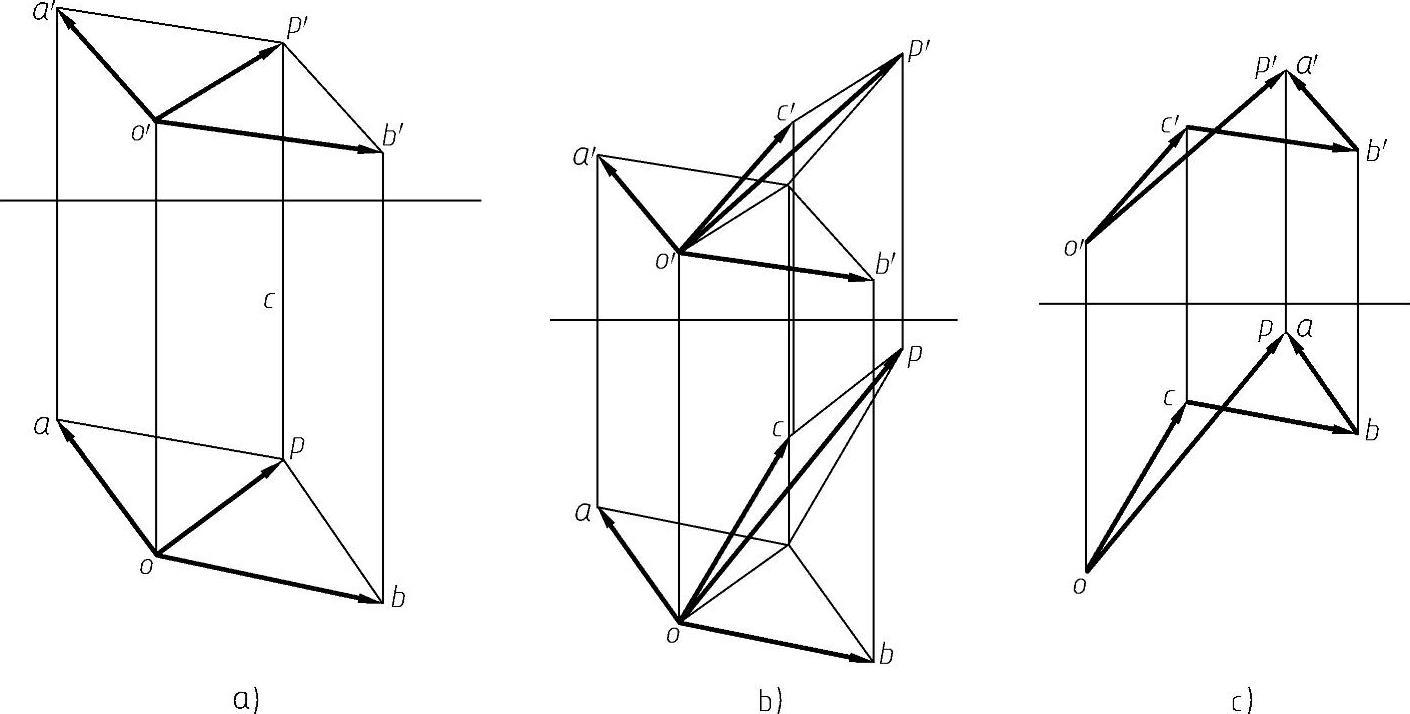
图8-4 力的合成

a）两个力的平行四边形法合成 b）三个力的平行四边形法合成 c）三个力的力多边形法合成