直齿锥齿轮背锥及其应用

锥齿轮传动用来传递两相交轴之间的运动和动力，轴交角Σ可根据传动需求来确定，一般多采用Σ=90°。锥齿轮的轮齿分布在一个圆锥上，这是它区别于圆柱齿轮的主要地方。

一对锥齿轮传动时，其锥顶交于一点O，在距锥顶O不等的截面上的轮齿大小不等，锥齿轮的轮齿是自大端向锥顶收缩的。为计算和测量的方便，通常研究大端的齿形，并取大端的齿形参数为标准值。

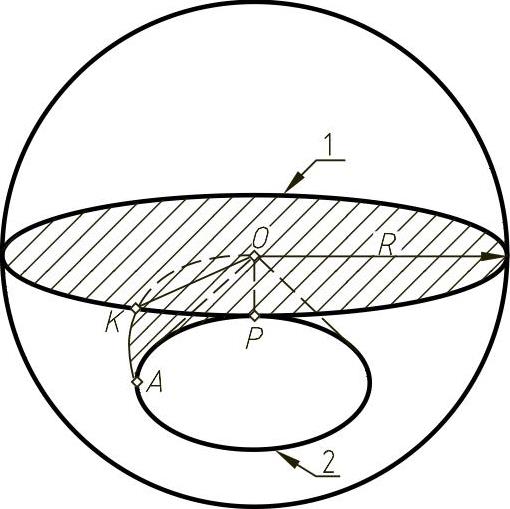
齿轮传动中，两齿轮绕各自的轴线回转，显然，只有与锥顶O等距的对应点才能相互啮合，故锥齿轮的共轭齿廓应分布在以锥顶O为球心的球面上。锥齿轮的齿廓曲面应为渐开线锥面。渐开线锥面的形成方法如图7-25所示。平面1在基圆锥2上作纯滚动时，该平面上过锥顶O的任一直线OK的轨迹即为渐开线锥面。该锥面与以O为球心，以锥距R为半径的球面的交线为球面渐开线，如图中的曲线AK，它应是锥齿轮的大端齿廓曲线。但球面无法展开成平面，这样，锥齿轮的设计计算就产生了困难，为此应寻求一种代替球面渐开线的近似的计算方法。

(www.xing528.com)

图7-25 渐开线锥面的形成方法

图7-26所示为一锥齿轮的轴剖面图，其中△OAA代表分度圆锥，△Obb代表齿顶圆锥，△Occ代表齿根圆锥。r为分度圆半径，以锥顶O为圆心，以OA为半径的圆应为球面的投影，若以球面渐开线作锥齿轮的齿廓，则圆弧bAc即为齿轮大端与轴剖面的交线，该球面曲线是不能展开成平面的。

过齿轮大端上A点作球面的切线O₁A，与齿轮的轴线交于O₁点。设想以OO₁为轴线，以O₁A为母线形成的回转面也为圆锥面，它与锥齿轮大端切于A点，称为锥齿轮的背锥。△O₁AA即为背锥在锥齿轮轴剖面上的投影。由于背锥母线O₁A与锥齿轮的分度圆锥母线相互垂直，将球面渐开线投影到背锥上得到的点b′、c′分别与球面渐开线上的b和c点非常接近，故可用背锥上的齿形近似地作为锥齿轮的大端齿形。