透视基本原理与程序示意图

进行透视投影要考虑好图面布局，以避免立体的平面或直线积聚成直线或点而影响直观性。具体地说，就是要考虑以下几点：

1）立体与画面的相对位置。

2）视距，即视点与画面的距离。

3）视点的高度。

1.一点透视

作一点透视的具体步骤是：先将立体平移到适当位置，再进行透视变换，然后向画面作正投影，这可以将平移矩阵、透视变换矩阵及向XOY面的正投影变换矩阵级联而实现。这三个矩阵级联后形成一点透视变换矩阵T₁，即

若某点的坐标为[x，y，z]，它的一点透视变换可写成

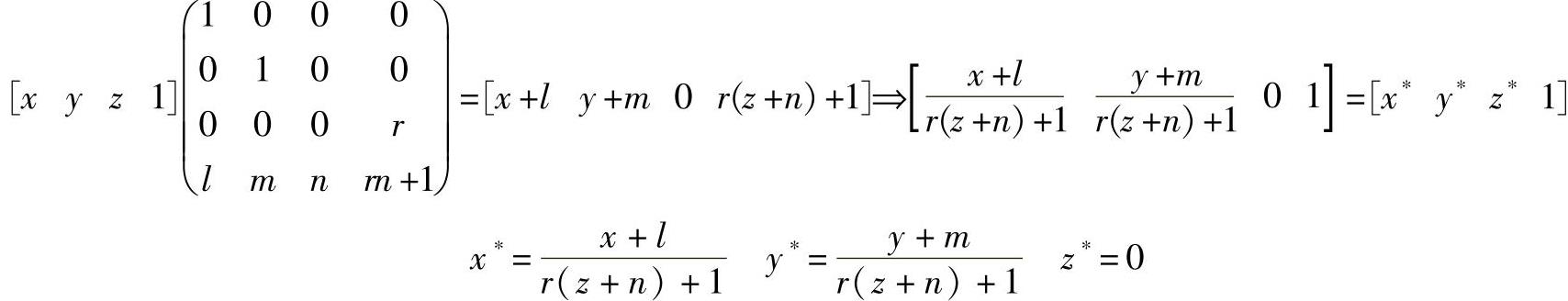
式中 l——将立体沿X方向移动的距离；

m——将立体沿Y方向移动的距离；

n——将立体沿Z方向移动的距离；

r——视点取在Z轴上，使视距d=-1/r。

对相机而言，视距即为相机焦距，由相机所定，z可以理解为物体与画面的距离，画面即相机胶片平面，相机透镜中心是投射中心，设为坐标原点。

例如，当l=0.8，m=-1.6，n=-2，r=-0.4时，求立方体的一点透视。

用矩阵级联的方法，即

一点透视的各点坐标也可以用公式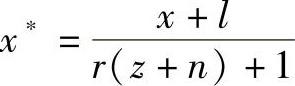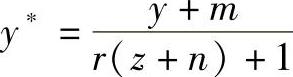，来求，当各参数条件不变，可算得立方体各点在透视图上的坐标与用矩阵级联的方法算得的结果相同。将透视图各点计算公式变换为

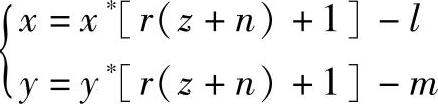
设z为自变量，将已知立方体各点在透视图上的坐标代入上式，即可求得立方体各点的空间坐标。

当z_a=0时

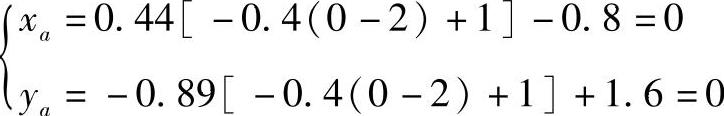
当z_b=0时

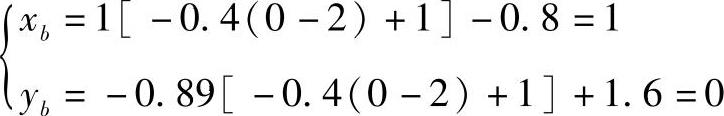
当z_c=0时

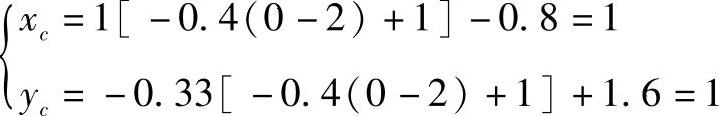
当z_d=0时

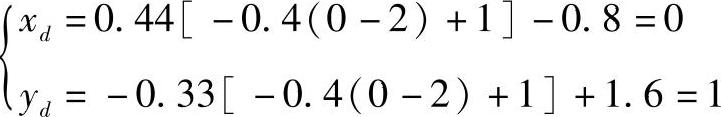
当z_e=1时

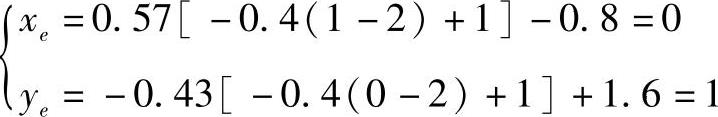
当z_f=1时

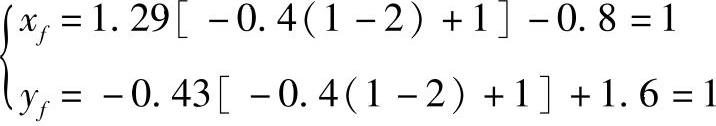
当z_g=1时

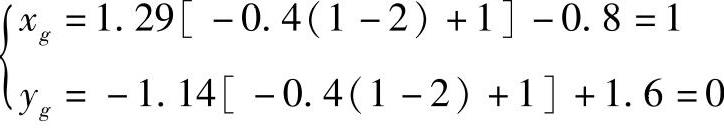
当z_h=1时

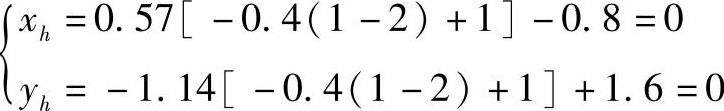
一点透视程序LP6-13.lsp可通过扫描二维码观看，程序运行后得到的图形如图6-28所示。

LP6-13.lsp程序

图6-28 一点透视程序运行后得到的图形

2.两点透视

两点透视的特点是平行六面体在作了透视变换后，只有垂直方向棱线的投影仍是互相平行的，另外两个方向棱线的投影分别交于灭点。作两点透视时要将立体绕Y轴旋转一个φ角，使立体的主要平面不平行于画面，经透视变换，使立体产生变形，然后向画面作正投影，如图6-26所示。如果立体的底面置于XOZ平面上，这时按上述步骤得到的透视，其底面积聚成一条直线，直观性较差，为此，必须先将立体作适当平移。其一般步骤如下：

1）将立体平移到适当位置，使视点有一定高度，且使立体的主要表面不会积聚成线。

2）将立体绕Y轴旋转一个φ角，一般使转角φ＜90°，旋转方向仍按右手规则。

3）进行透视变换，使立体产生变形。为了符合人的视觉，使变形后的立体渐远渐小，一般使p＜0，r＜0。

4）经上述变换后，向画面（XOY）进行正投影，即得透视。(www.xing528.com)

上述步骤用矩阵表示，则得两点透视变换矩阵T₂，即

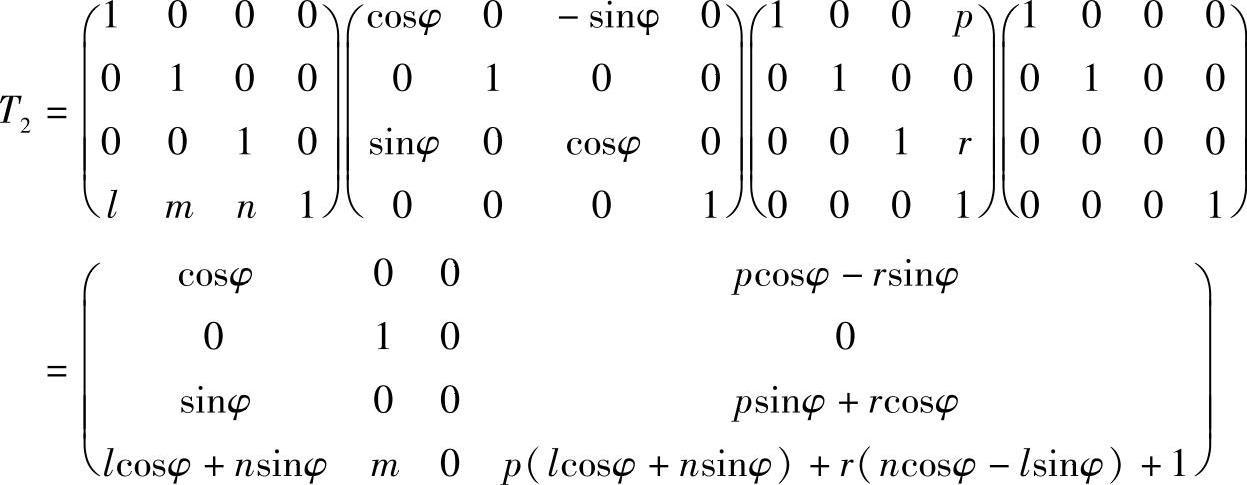
对空间各点作两点透视，其在透视图上的坐标也可写为

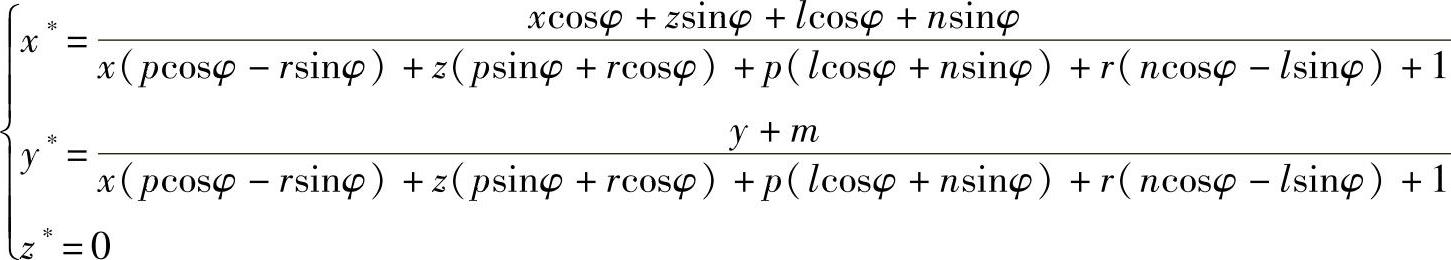
当已知p=-0.1，q=0，r=-0.45，φ=30°，l=n=0，m=-1.4时，有

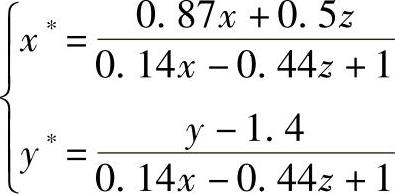
当z=0时，有

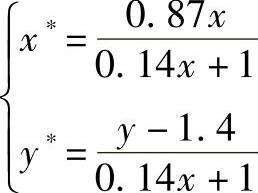
当z=1时，有

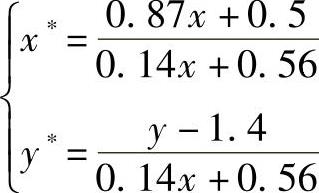
对立方体而言，其各点的空间坐标与透视图坐标分别为

设z为自变量，根据立方体各点透视图坐标反求其空间坐标的公式为

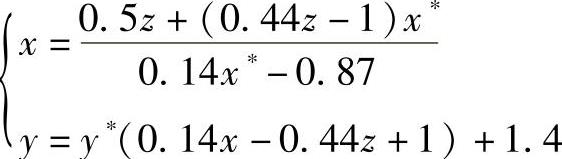
当z=0时，有

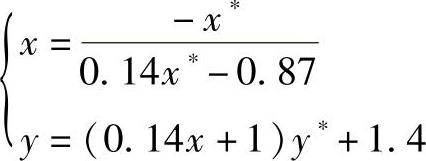
当z=1时，有

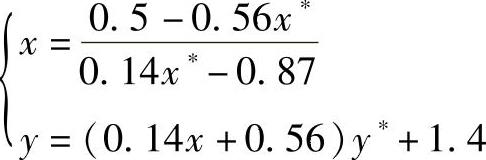
将立方体各点A^∗、B^∗、C^∗、…透视图坐标代入反求公式，即可得立方体各点A、B、C、…的空间坐标，请读者自行验证。

两点透视程序LP6-14.lsp可通过扫描二维码观看，程序运行后得到的图形如图6-29所示。

3.三点透视

三点透视就是有三个灭点的透视，如图6-27所示，这时，透视变换矩阵中的元素p、q、r都不等于零。平面六面体在三点透视图中三个方向的棱线分别汇交于三个不同的灭点。作三点透视的步骤如下：

1）将立体平移到适当位置。

2）将立体进行透视变换。

3）使立体先绕Z轴旋转θ角，再绕X轴旋转φ角。

LP6-14.lsp程序

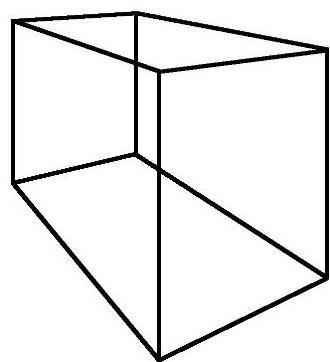
图6-29 两点透视程序运行后得到的图形

4）将变形而又旋转后的立体向画面进行正投影即得三点透视图。

用变换矩阵来表示上述作图过程，就得到三点透视变换矩阵T₃，即

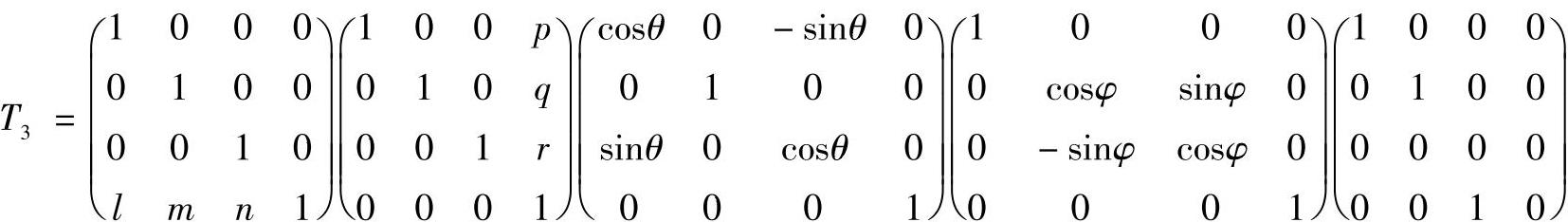
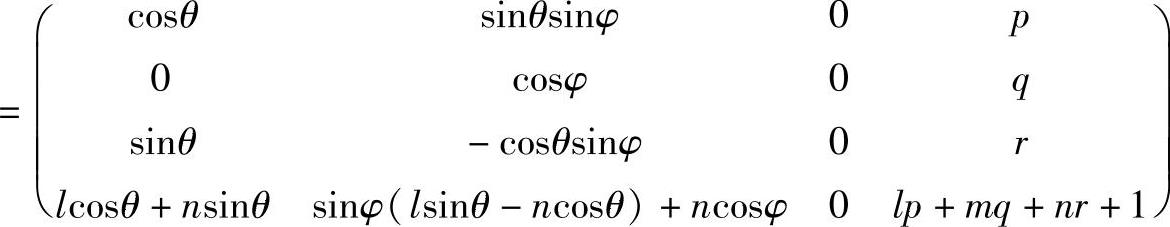
即有

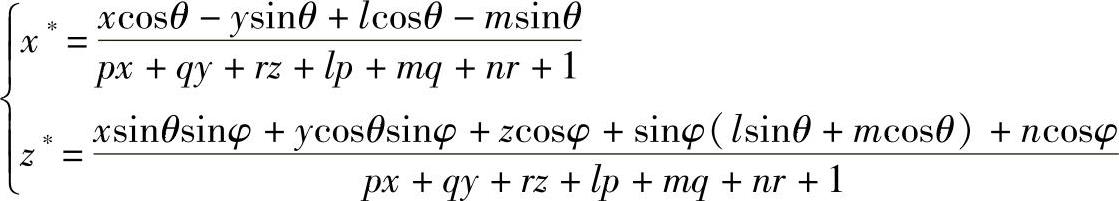
当p=-0.3，q=-0.3，r=0.35，θ=30°，φ=30°，l=-1，m=-1，n=-1.5时，有

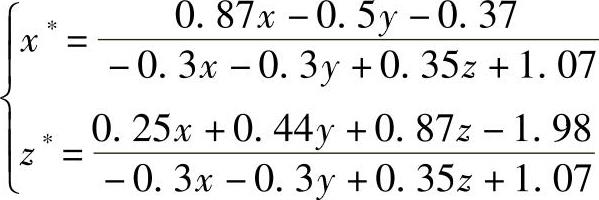
立方体各角点经透视变换后由A、B、…、H变为A∗、B∗、…、H∗，即有

三点透视投影变换公式是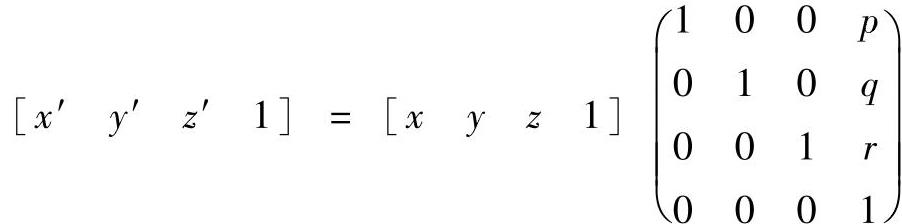，若投射中心在X轴的p_x处、Y轴的p_y处和Z轴的P_z处，则p=-1/p_x，q=-1/p_y，r=-1/p_z。通常一点透视投影变换r≠0，p=q=0；两点透视投影变换p、q、r中有一个数为零，其余两个数为非零；在三点透视投影变换中p、q、r均为非零。

三点透视程序LP6-15.lsp可通过扫描二维码观看，其程序运行后得到的图形如图6-30所示。

LP6-15.lsp程序

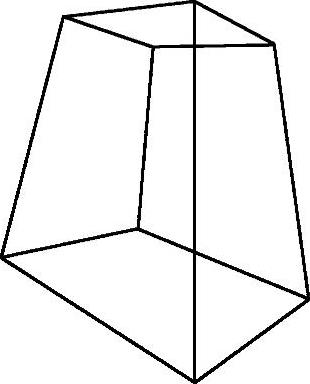
图6-30 三点透视程序运行后得到的图形