图6-22a所示是一建筑物的照片,照片上的成像是失真的,但人的感觉却是自然亲切的,这是因为照片的拍摄过程与人眼看物体时,在人眼视网膜上成像的变化是相似的。为了准确地画出这种具有明显的空间立体感的图像,过去的画家往往设想透过透明的纱面或玻璃来观看物体,将所见到的形体轮廓直接描绘在纱面或玻璃上。因此,很久以来就一直将近大远小这种特征的图像称为透视图或透视投影,简称为透视。从投影法来说,透视图就是以人眼为投射中心的中心投影。图6-22b表示了中心投影的基本要素。
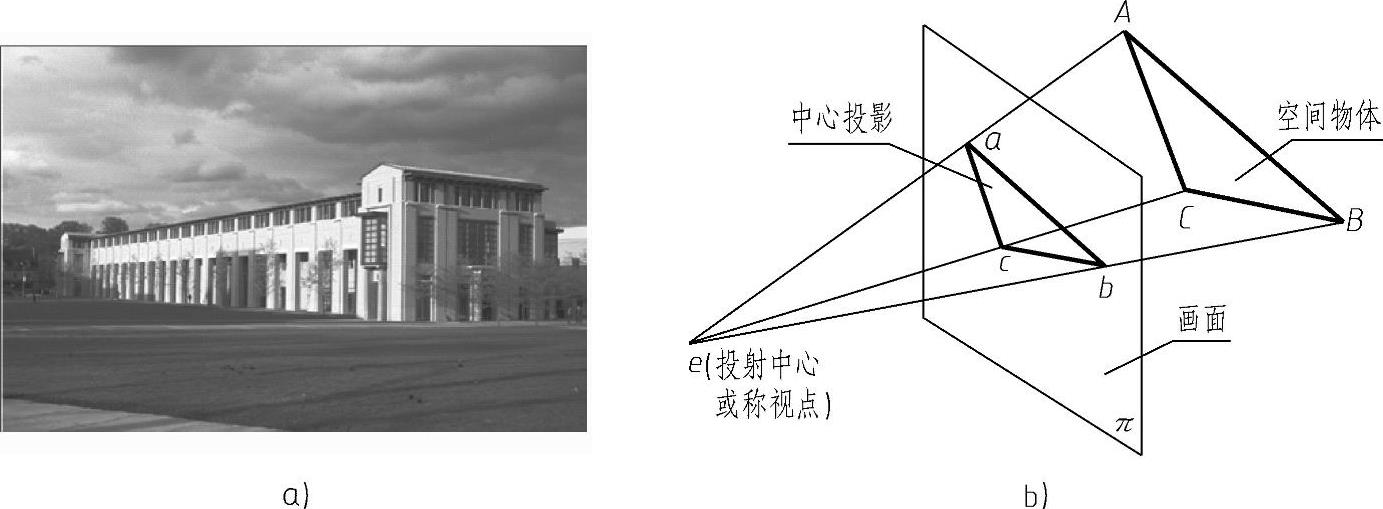
图6-22 照片与透视投影
a)照片 b)透视投影
在绘制透视图时常用到一些专门术语,必须弄清楚它们的确切含意,这样有助于理解透视的形成过程。结合图6-23介绍透视作图中的几个基本术语。
基面——放置物体的水平面,以字母G表示。
画面——透视图所在的平面,以字母P表示,一般以垂直于基面的铅垂面为画面。
基线——基面与画面的交线,在画面上以字母g-g表示,在平面中则以p-p表示画面的位置。
视点——相当于人眼所在的位置,即投射中心S。
站点——视点S在基面G上的正投影s,相当于观看物体时人的站立点。
心点——视点S在画面P上的正投影s°。
中心视线——引自视点并垂直于画面的视线,即视点S和心点s°的连线Ss°。
视平面——过视点S所作的水平面。
视平线——视平面与画面的交线,以h-h表示,当画面为铅垂面时,视平线与基线的距离反映视高。
视距——视点对画面的距离,即中心视线Ss°的长度,当画面为铅垂面时,站点与基线的距离反映视距。
图6-23中,点A是空间任意一点,自视点S引向点A的直线SA,就是通过点A的视线;视线SA与画面的交点A°,就是空间A点的透视;点a是空间点A在基面上的正投影,称为A的基点;基点的透视a°,称为点A的基透视。(https://www.xing528.com)
透视图的一个重要特性就是,在透视图中,空间相互平行两直线的投影可以不平行且相交于一点,这种点称为灭点,如图6-24所示。
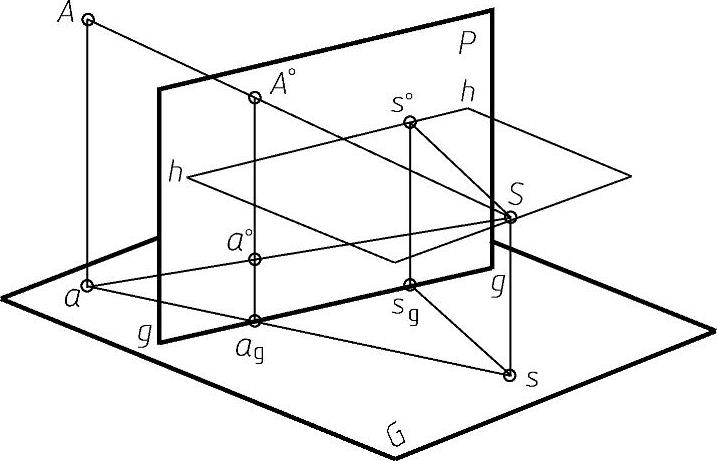
图6-23 透视常用术语
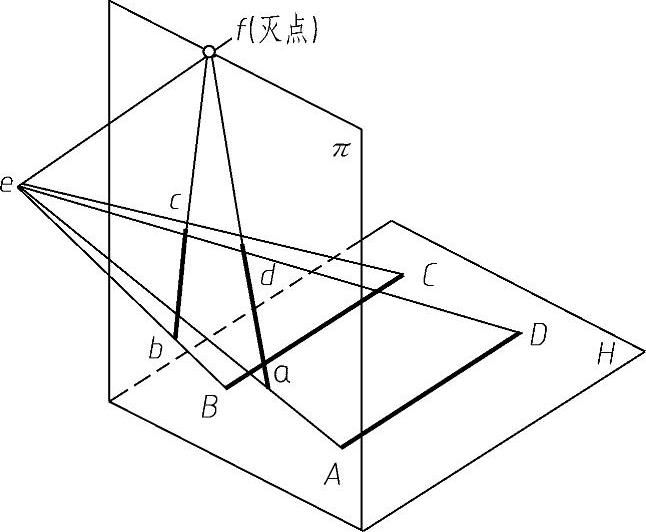
图6-24 透视图的重要特性
一个长方体由于它与画面间相对位置的变化,其长、宽、高三组主要方向的轮廓线,与画面可能平行,也可能倾斜。与画面倾斜的轮廓线,在透视图中会形成灭点;而与画面平行的轮廓线,在透视图中就没有灭点。因而,透视图一般就按照画面上灭点的多少分为以下三种。
(1)一点透视 如果长方体有两组轮廓线平行于画面,那么这两组轮廓线的透视图就不会有灭点,而第三组轮廓就必然垂直于画面,其灭点就是心点s°,如图6-25所示。这样画出的透视图称为一点透视。
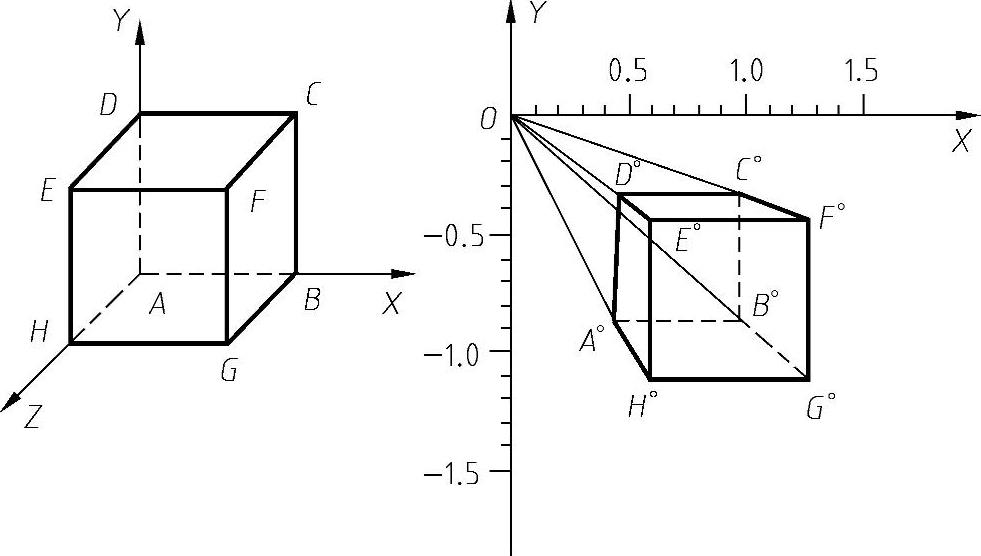
图6-25 长方体的轴测图和一点透视
(2)两点透视 如果长方体仅有铅垂轮廓与画面平行,而另外两组水平的轮廓线均与画面斜交,于是画面上形成了两个灭点FX及FY,这两个灭点都在视平线h-h上,如图6-26所示。这样画成的透视图称为两点透视。
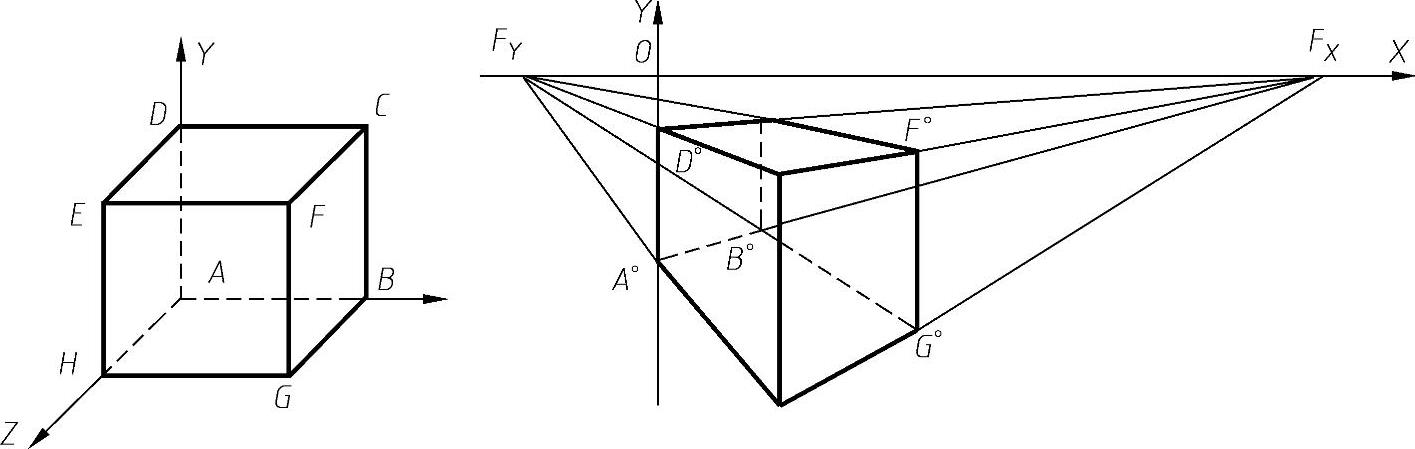
图6-26 长方体的轴测图与两点透视
(3)三点透视 如果画面倾斜于基面,即与长方体三组轮廓线均相交,这样,在画面上就会形成三个灭点,如图6-27所示。这样画出的透视图称为三点透视。
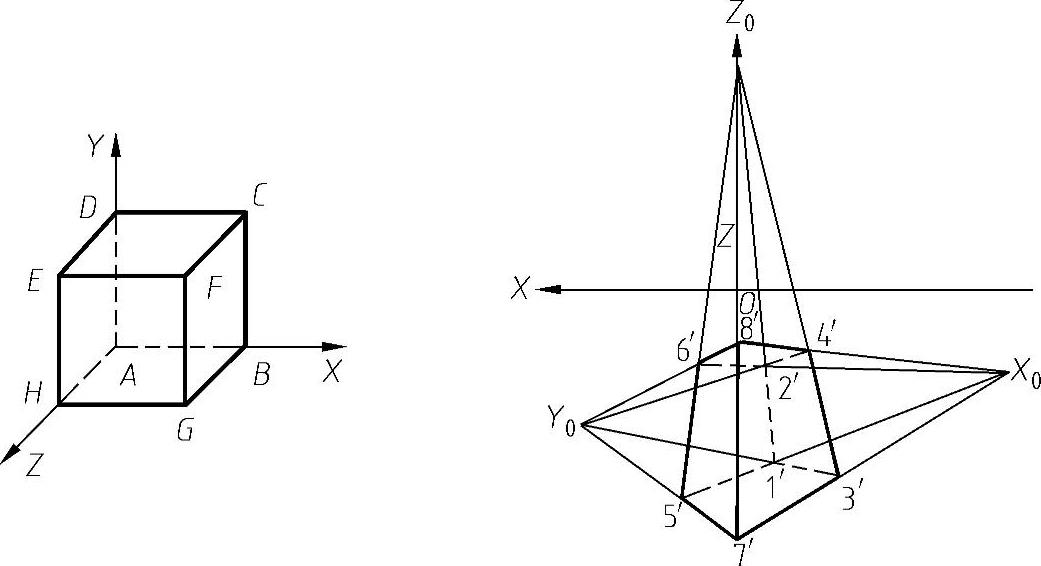
图6-27 长方体的轴测图和三点透视
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




