正轴测投影图的反求建模-正轴测投影图反求建模

为根据任意观察方向下的正轴测投影图来反求物体的大小，以图6-2所示物体为例，根据图6-2a所注的尺寸，可得图6-3a所示物体的各点坐标。图6-2b所示为新设的投射方向；图6-3b所示为新设投射方向对应的正轴测投影图；图6-3c所示为转正位置后的正轴测投影图。

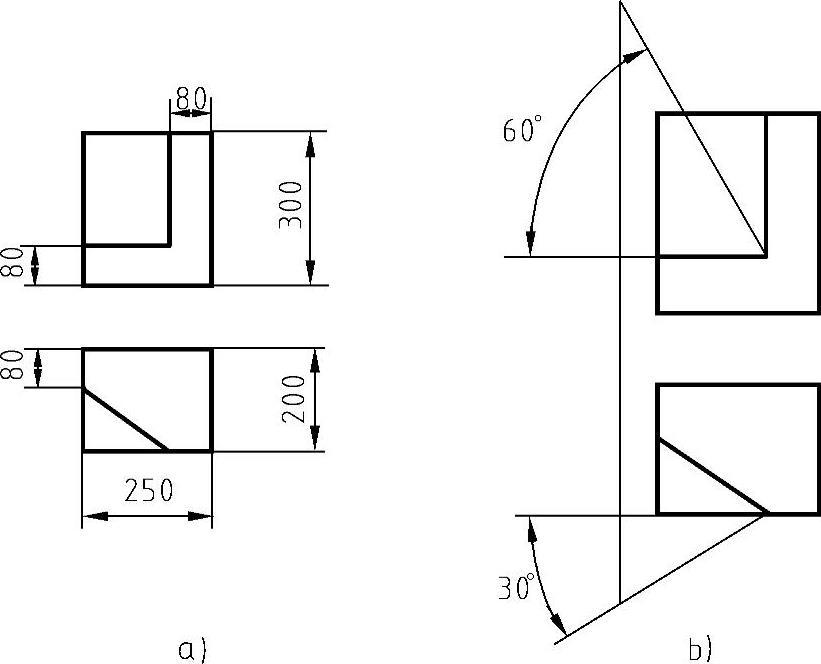
图6-2 物体的投影

a）物体的两个视图 b）新投射方向

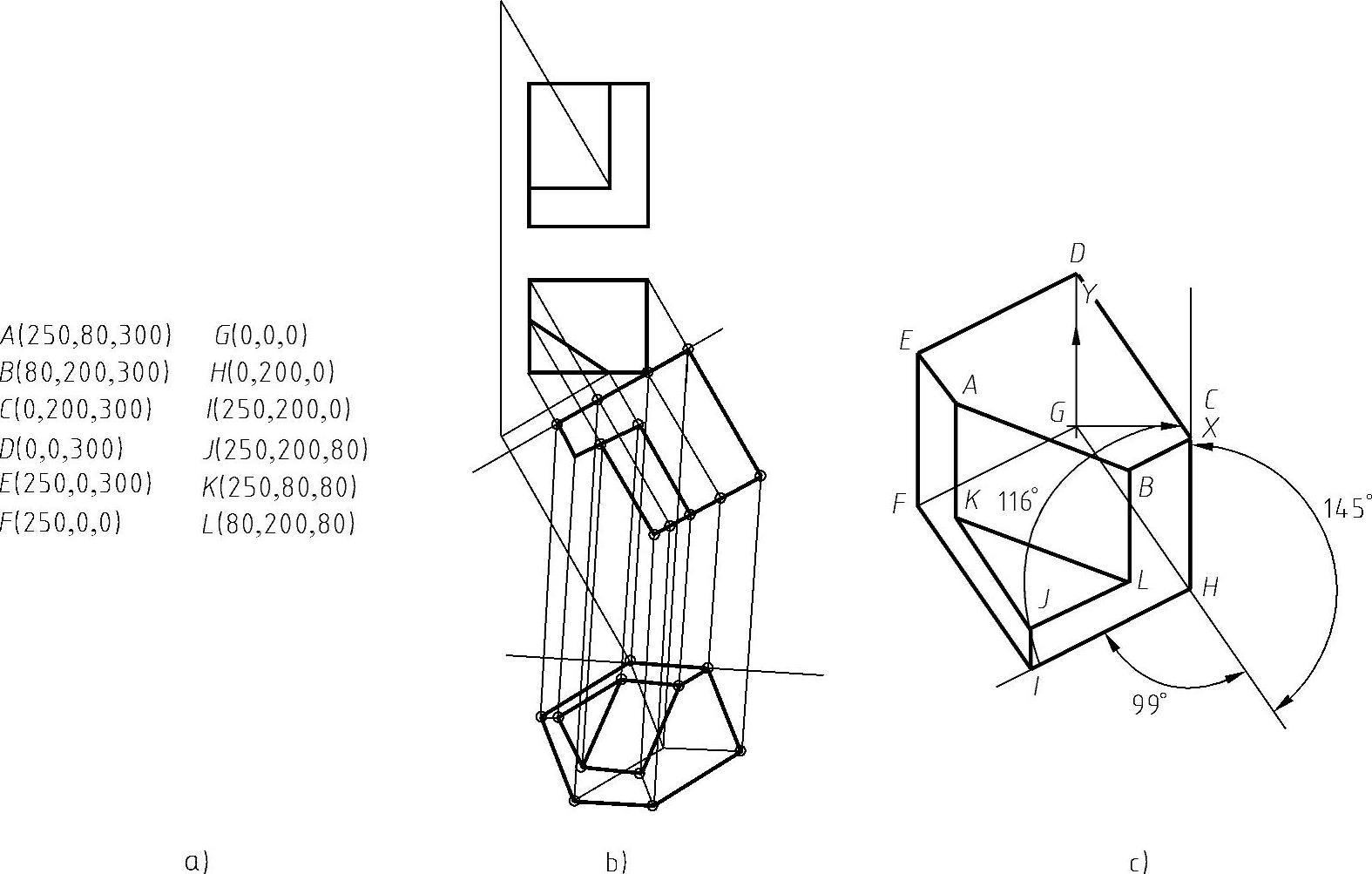
图6-3 投影变换获得的正轴测投影图

a）物体上各点的坐标 b）正轴测投影原位图 c）转正位置后的正轴测投影图

利用第1章中一般位置直线变换为投影面垂直线的数学公式式（1-13）和式（1-14）编制绘图程序LP6-1，并运行，得到物体正轴测投影图形的各点坐标及轴测投影图，如图6-4a、b所示。

利用式（6-1）～式（6-6）编制程序LP6-2，计算观察方向为φ=60°、β=30°时的轴向伸缩系数和轴间角，结果如图6-4c所示。如果将一般位置直线当作视线，当将视线变换为投影面垂直线时，其所垂直的投影面就是正等轴测投影面，因此根据式（1-13）、式（1-14），结合图1-46可以得出已知新投影（正轴测投影）的坐标，反求其在原空间坐标系中的坐标（原投影体系的投影）的计算公式为

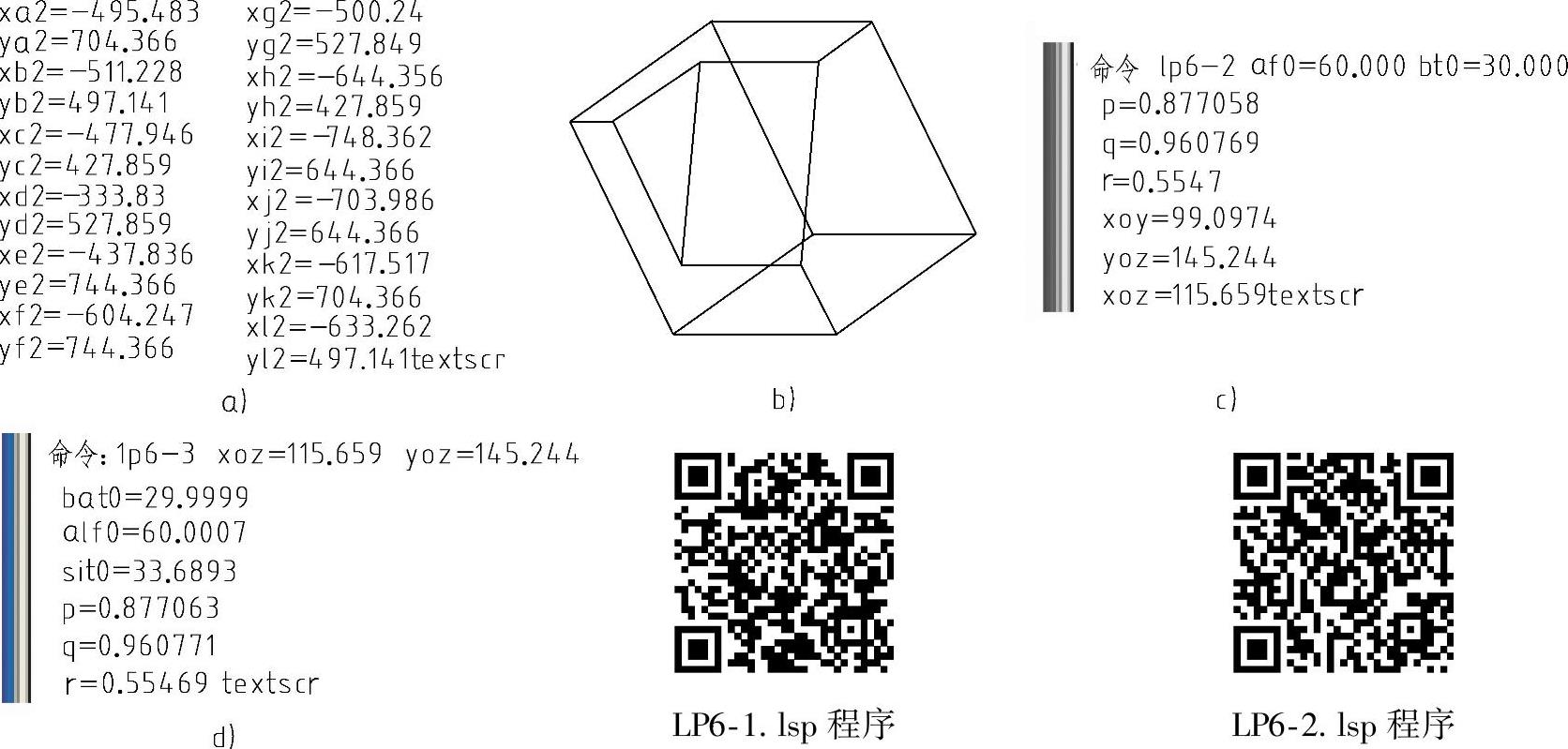
图6-4 轴测投影图二维坐标与反求得出的投影角及轴向伸缩系数

a）二维坐标 b）轴测投影图 c）由观察方向得出的轴向伸缩系数、轴间角 d）反求得出的投影角与轴向伸缩系数

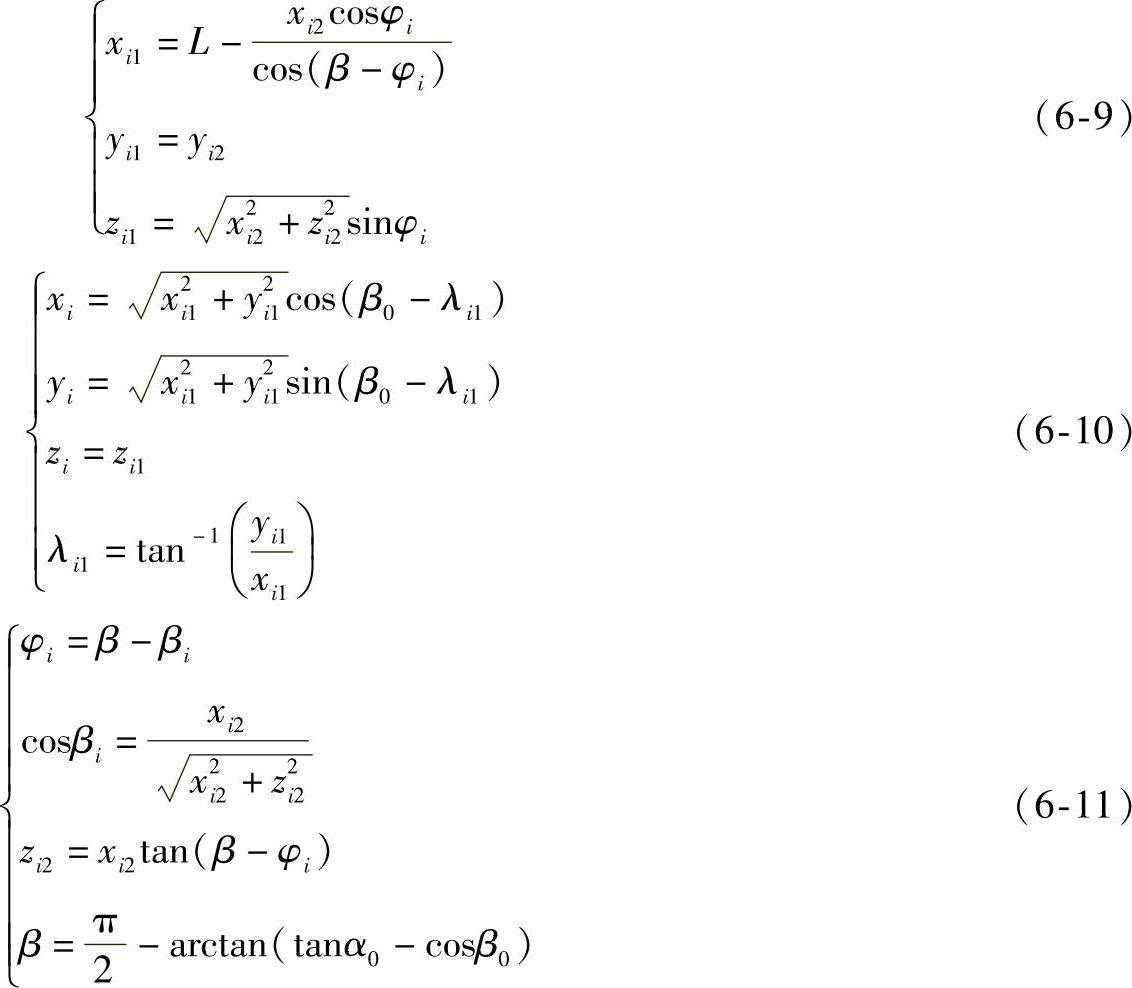
根据正轴测投影的轴间角，反求伸缩系数、投射方向的公式式（6-4）～式（6-6），编制程序LP6-3计算并打印出投影角与轴向伸缩系数，如图6-4d所示，应用图6-4a中的二维坐标，根据式（6-9）～式（6-11）编制程序LP6-4反求三维点坐标，并绘制物体的三维图形，如图6-5所示。

由图6-4c可知，反求所得的轴间角、轴向伸缩系数、投射方向与原始条件是一致的。由图6-5a中的各点坐标可计算图6-2a所示尺寸(www.xing528.com)

长度方向的尺寸为

LP6-3.lsp程序

LP6-4.lsp程序

图6-5 物体的三维图形

a）反求得出的三维坐标 b）三维图形

宽度方向的尺寸为

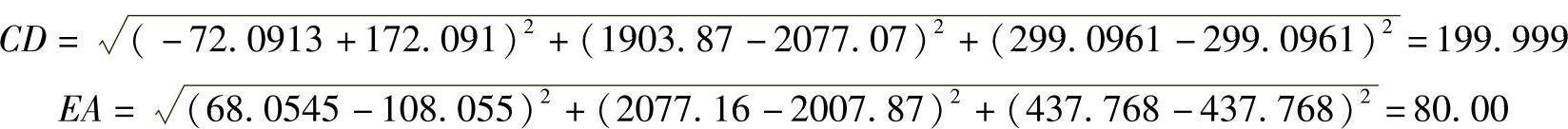
高度方向尺寸为

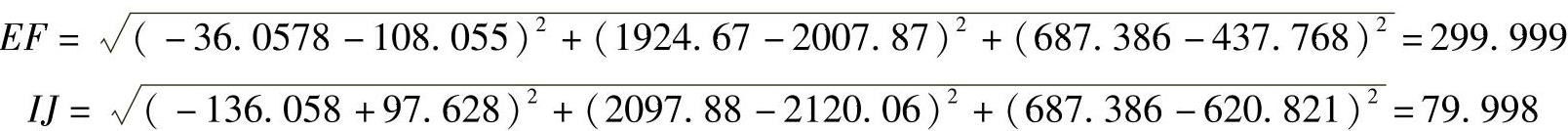
如忽略不计计算误差，可见反求结果与原尺寸相同。图6-5b所示是物体的三维线框图，可以通过旋转、移动获得各个方向的图形。本例是为了说明反求的正确性，给出了物体的主俯视图和尺寸，如果一开始就用轴测投影图进行设计，就须先根据轴间角由式（6-6）反求出β、θ，再由式（6-2）反求出φ角，然后才能按照上面的反求步骤求得实形，再造型后生成二维工程图。本例中四个程序LP6-1.lsp～LP6-4.lsp可分别通过扫描二维码观看。