计算机实验工程图形学.轴向伸缩系数

在1.5.1节中，用投影变换方法建立观察模型的实验中采用先选合适的观察方向，再应用换面法或旋转法获得立体感图形，所得到的立体感图形实际上就是正轴测投影图。因此，可选择投影变换的方法分析轴向伸缩系数与轴间角之间的关系，把物体上的坐标系OIJK的原点置于x轴并取OI=OJ=OK=e（e为单位长），使投射方向过原点O，设投射线S在空间坐标系中的位置由φ、β角确定，如图6-1所示。

一次投影变换将S变为正平线（应有x₁//S）。为简单起见，使x₁轴过S的水平投影s，并过原点O，物体上坐标系OIJK也随之变换为O₁I₁J₁K₁。二次变换将投射方向变换为铅垂线，此时新投影轴x₂必垂直于o′₁s′₁交x₁轴于o₂，设x₁轴与x₂轴的夹角为θ，由图6-1可知，θ、φ、β之间的关系为

得

θ=arccot（cosβtanφ） （6-2）

物体上坐标系O₁I₁J₁K₁也随之变换为O₂I₂J₂K₂。注意，x₂轴的方向与o₁′s₁′垂直，但x₂轴的位置不是唯一的，图中位置是为图形清晰起见而设，而为使寻求投射方向、轴向伸缩系数、轴间角之间的关系容易起见，可将y₂轴平移，使O₂与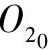重合。这时由图6-1可得I、J、K三点在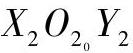坐标面中的坐标为

由于x₂O₂y₂即为正轴测投影面，而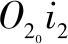、、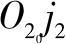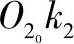即为轴测轴，因此可得轴向伸缩系数为

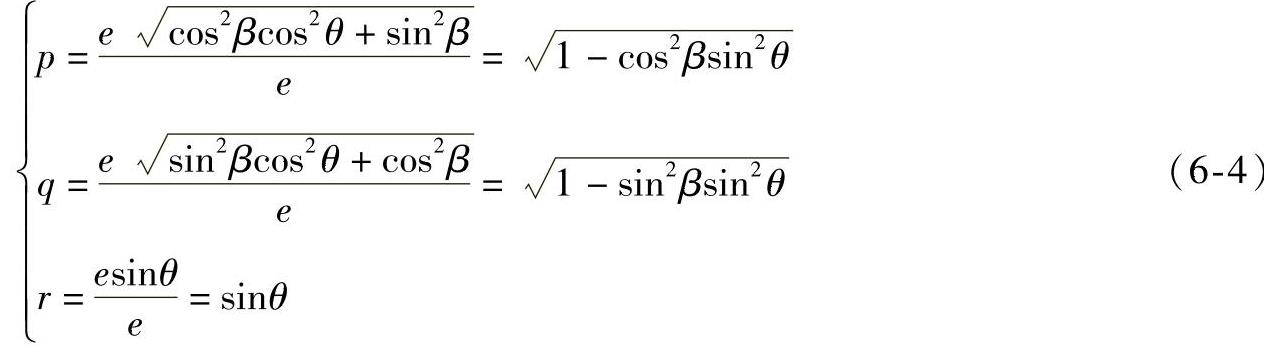(www.xing528.com)

由式（6-4）即可得

p²+q²+r²=2 （6-5）

式（6-5）表明正轴测投影三个轴向伸缩系数的平方和恒等于2。而由图6-1可知，轴间角为

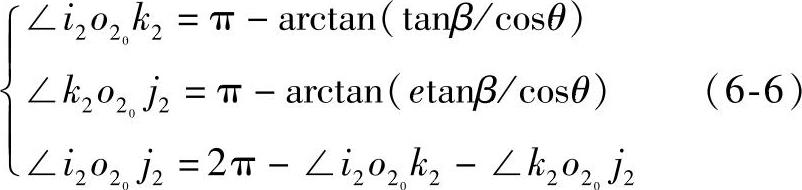
由于θ为β、φ的函数，故轴向伸缩系数、轴间角与投射方向之间的关系即为式（6-4）～式（6-6）。根据这组公式就能计算出任何一种形式正轴测投影体系中投射线的正投影与坐标轴所夹角度的大小。也可以由已选定的β、φ角计算出正轴测投影体系的各轴向伸缩系数。解决了投射方向与轴间角、轴向伸缩系数之间的关系后，结合将一般位置直线变换为投影面垂直线的数值解所述内容，即可得正轴测投影图的数值解的方法。

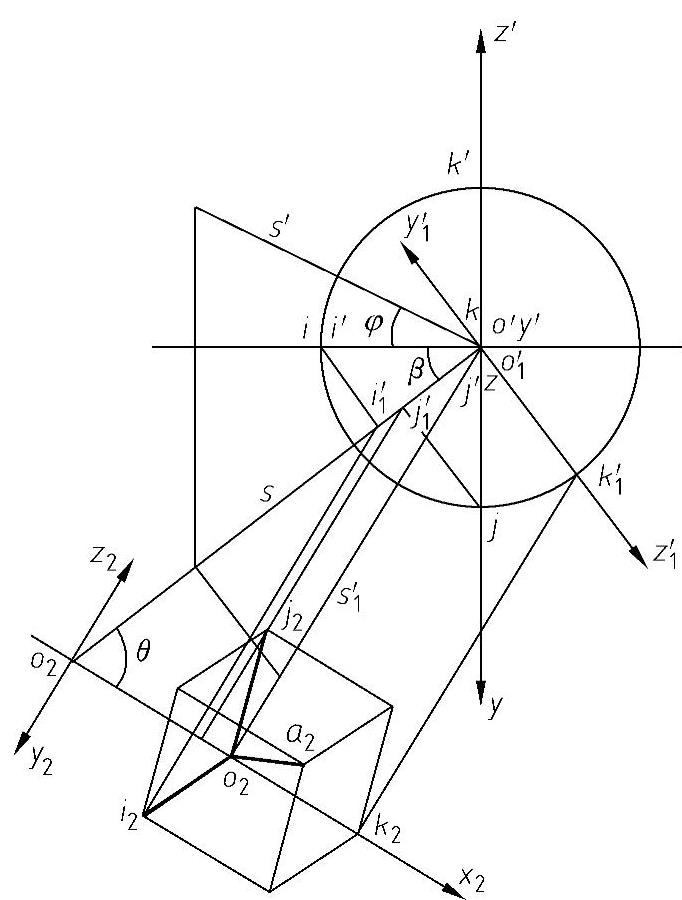
图6-1 正等轴测投影轴间角、轴向伸缩系数的关系