物理量图形表示，计算机实验工程图形学

1.轴力与轴力图

沿着杆件轴线方向作用的载荷，通常称为轴向载荷。杆件承受轴向载荷作用时，横截面上只有一种内力分量——轴力，用F_N表示。杆件只在两个端面处承受轴向载荷时，则杆件的所有横截面上的轴力都是相同的。如果杆件上作用有两个以上的轴向载荷，就只有两个轴向载荷作用点之间的横截面上的轴力是相同的。轴力相同的一段杆的两个端截面称为控制面。表示轴力沿杆件轴线方向变化的图形称为轴力图。为了绘制轴力图，杆件上同一处两侧横截面上的轴力必须具有相同的正负号。因此，约定使杆件受拉的轴力为正，受压的轴力为负。绘制轴力图的方法如下：

1）确定约束力。

2）根据杆件上作用的载荷及约束力，确定控制面，也就是轴力图的分段点。

3）应用截面法，用假想截面从控制面处将杆件截开，在截开的截面上，画出未知轴力，并假设为正方向；对截开的部分杆件建立平衡方程，确定控制面上的轴力数值。

4）建立F_N-x坐标系，将所求得的轴力值标在坐标系中，画出轴力图。

例5-1 已知阶梯形直杆AE受力如图5-5a所示，试计算各段轴力，并画出轴力图。

解 （1）确定约束力 A处虽然是固定端约束，但由于杆件只有轴向载荷作用，所以只有一个轴向的约束力F_A。由平衡方程∑F_x=0求得∑F_A=40kN，F_A的方向如图5-5b所示。

（2）确定控制面 在A处约束力、B处集中载荷作用处的A、B截面，以及B处集中载荷、D处集中载荷作用处的B、D截面，还有D处集中载荷、E处集中载荷作用处的B截面、E端面处的左右两侧为控制面，如图5-5b中虚线所示。

（3）应用截面法 采用截面法保留右端，则

F_NDE=-20kN

F_NBCD=（30-20）kN=10kN

F_NAB=（30+30-20）kN=40kN

（4）建立F_N-x坐标系，画轴力图 将所求得的各控制面上的轴力标在F_N-x坐标系中，所画的轴力图如图5-5c所示。

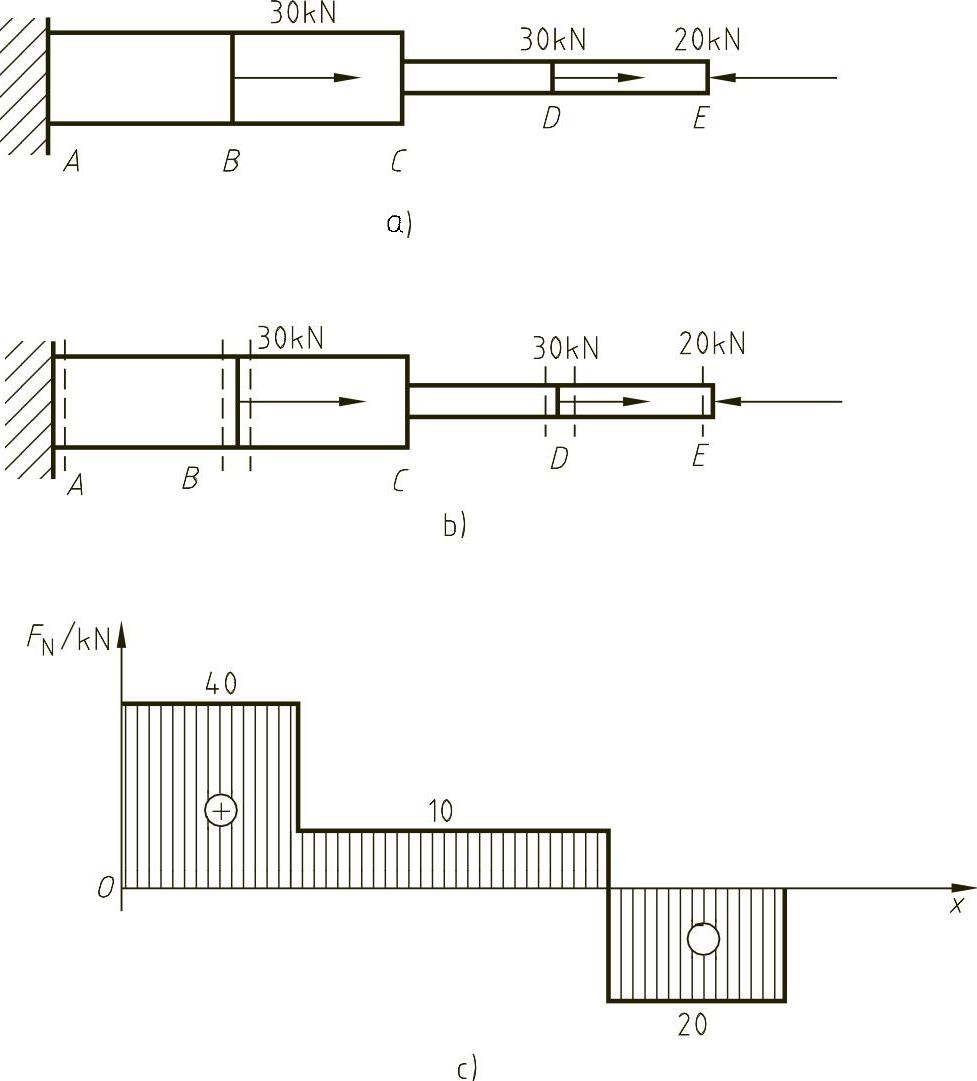
图5-5 例5-1图

画轴力图时应注意几点：①数值、单位；②正负号；③阴影线应与轴线垂直。另外，C处虽然截面面积有变化，但由于该处没有集中力作用，所以轴力图不会发生突变。

2.扭矩与扭矩图

图5-6所示是作用于圆轴上的外加扭转力偶矩，它与机器的转速、功率有关。在传动轴计算中，通常给出传动功率P和转速n，则传动轴所受的外加扭转力偶矩M_e可用下式计算

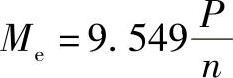
式中，P为功率（kW）；n为转速（r/min）。

确定圆轴横截面上的内力，仍然采用截面法。圆轴承受外加力偶作用后，其横截面上将产生一个连续分布的内力系，这一分布力系必组成一个力偶，与外加力偶平衡。横截面上的内力偶的力矩简称为扭矩，用T表示。根据杆截开后任一部分的平衡条件，即可由外加扭转力偶矩确定横截面上扭矩的大小和方向。对于只在两端承受外加扭转力偶的圆轴，应用截面法，如图5-7所示，考虑左边部分的平衡，由平衡条件得到其横截面上的扭矩等于外加扭转力偶矩，即

T=M_e

如果考虑右边部分的平衡，可以得到相同的结果，只是扭矩T的方向相反。

图5-6 作用在轴上的外加扭转力偶矩

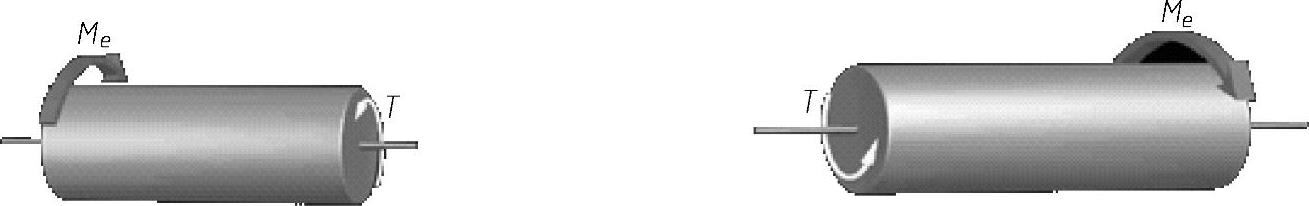
图5-7 截面法确定圆轴横截面上的扭矩

与规定轴力正负号原则相似，扭矩的正负号也是根据变形规定的，即同一横截面的扭矩具有相同的正号或者负号。据此，按右手螺旋法则确定扭矩的正负：如果扭矩矢量与横截面外法线方向一致，则扭矩为正；反之，为负，如图5-8所示。

图5-8 扭矩的正负号规则

当轴上作用有两个以上的外力偶时，其各段横截面上的扭矩一般不相等，这时需分段应用截面法，确定各段的扭矩。描述扭矩沿圆轴长度方向变化的图形称为扭矩图。画扭矩图的方法和过程与画轴力图相似：一般以圆轴轴线方向为横轴x，扭矩T为纵轴。

例5-2 如图5-9a所示，已知一传动轴的转速n=300r/min，主动轮A输入功率P_A=500kW，从动轮B、C、D输出功率P_B=P_C=150kW，P_D=200kW，试计算各段扭矩并画出扭矩图。

解 （1）计算外力偶矩M_e的大小

（2）求各段扭矩T（图5-9b）

BC段：T_BC=T₁=-M_B=-4.78kN·m

CA段：T_CA=T₂=-M_B-M_C=-9.56kN·m

AD段：T_AD=T₃=M_D=6.37kN·m

（3）画扭矩图 如图5-9c所示。

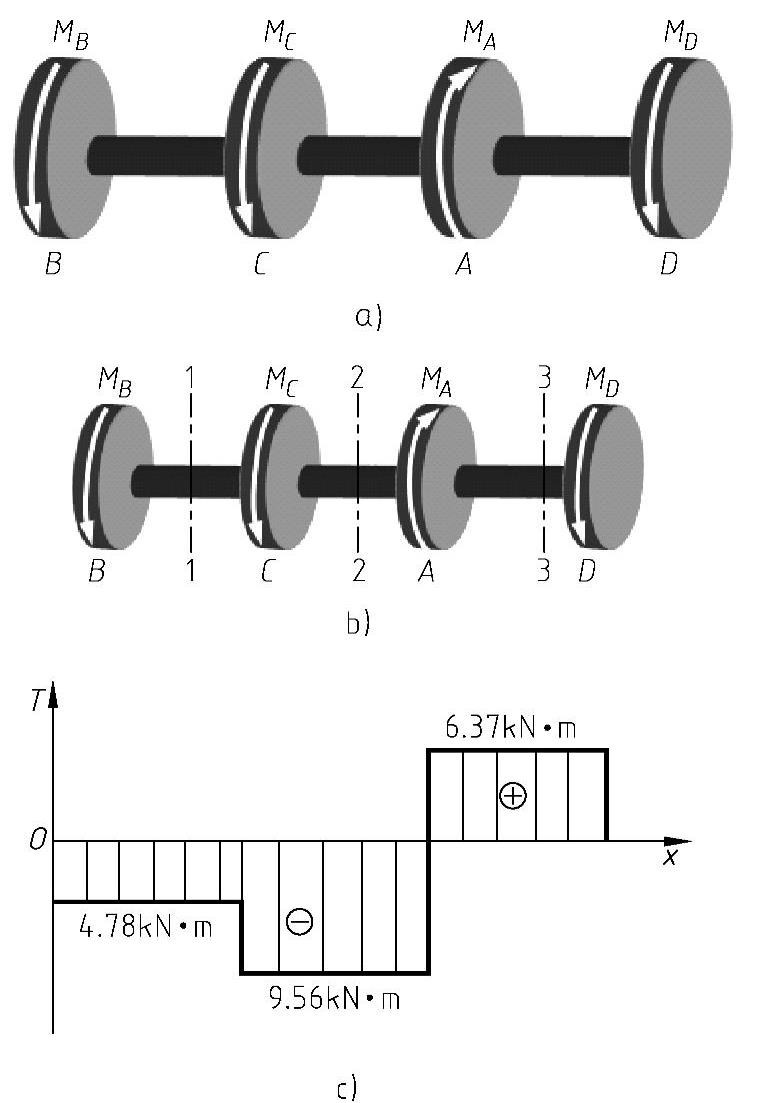
图5-9 例5-2图

注意：

1）沿杆件轴线各横截面上扭矩变化规律画扭矩图。

2）标注数值大小、单位和正负号。

3）阴影线垂直于横坐标，不是斜线。

4）封闭的实线图。

5）突变位置对应有外力偶作用。

3.剪力图与弯矩图

表示剪力与弯矩沿轴线方向变化的图线称为剪力图和弯矩图。绘制剪力图和弯矩图的方法是根据剪力方程和弯矩方程，在F_Q-x和M-x坐标系中标出分段点上的剪力值和弯矩值，得到相应的点；然后按照剪力方程和弯矩方程的类型，绘制出相应的图线，便得到所需要的图线。其过程与绘制轴力图和扭矩图的方法基本相同。其主要步骤如下：(www.xing528.com)

1）根据载荷与约束力的作用位置，确定分段点。

2）应用截面法确定分段点上的剪力和弯矩数值（包括正负号）。

3）分段建立剪力方程和弯矩方程。

4）建立F_Q-x和M-x坐标系，并将分段点上的剪力和弯矩值标在上述坐标系中，得到若干相应的点。

5）根据各段剪力方程和弯矩方程，在分段点之间绘制剪力图和弯矩图的图线，得到所需要的剪力图和弯矩图。

例5-3 如图5-10a所示，悬臂梁受均布载荷作用，试写出剪力和弯矩方程，并画出剪力图和弯矩图。

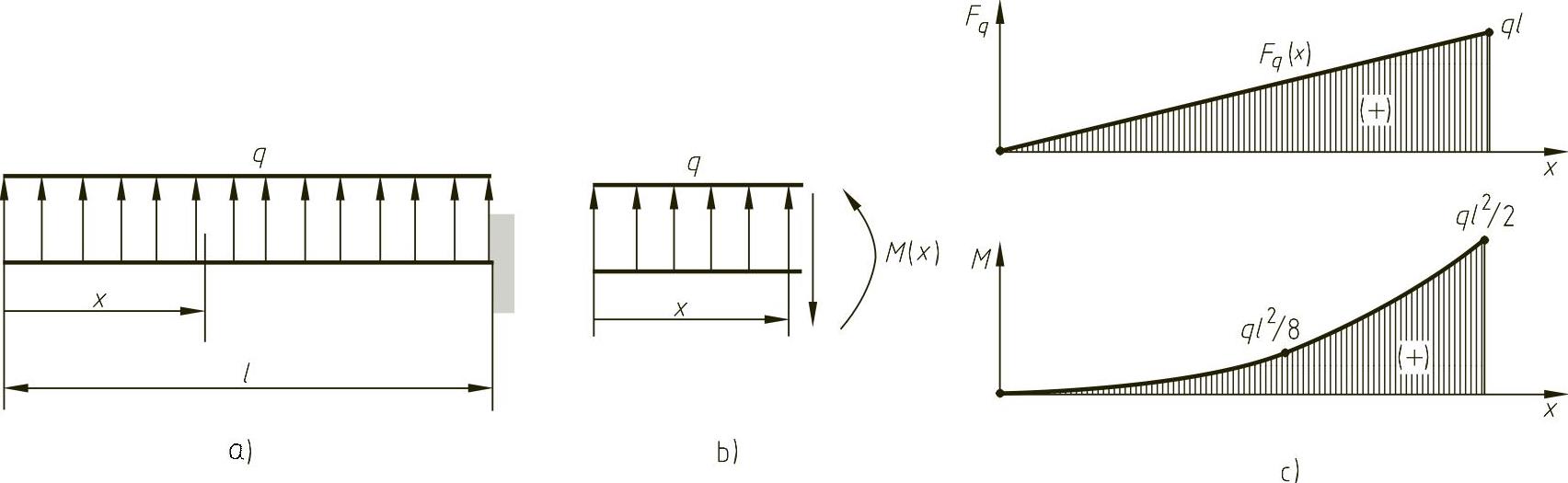
图5-10 例5-3图

解 任选一截面x，如图5-10b所示，写出剪力和弯矩方程

F_Q（x）=qx （0≤x＜l）

M（x）=qx²/2 （0≤x＜l）

依方程画出剪力图和弯矩图，如图5-10c所示，由剪力图、弯矩图可见，最大剪力和弯矩分别为

F_Qmax=ql

M_max=ql²/2

例5-4 试画出图5-11a所示有均布载荷的简支梁的剪力图和弯矩图。

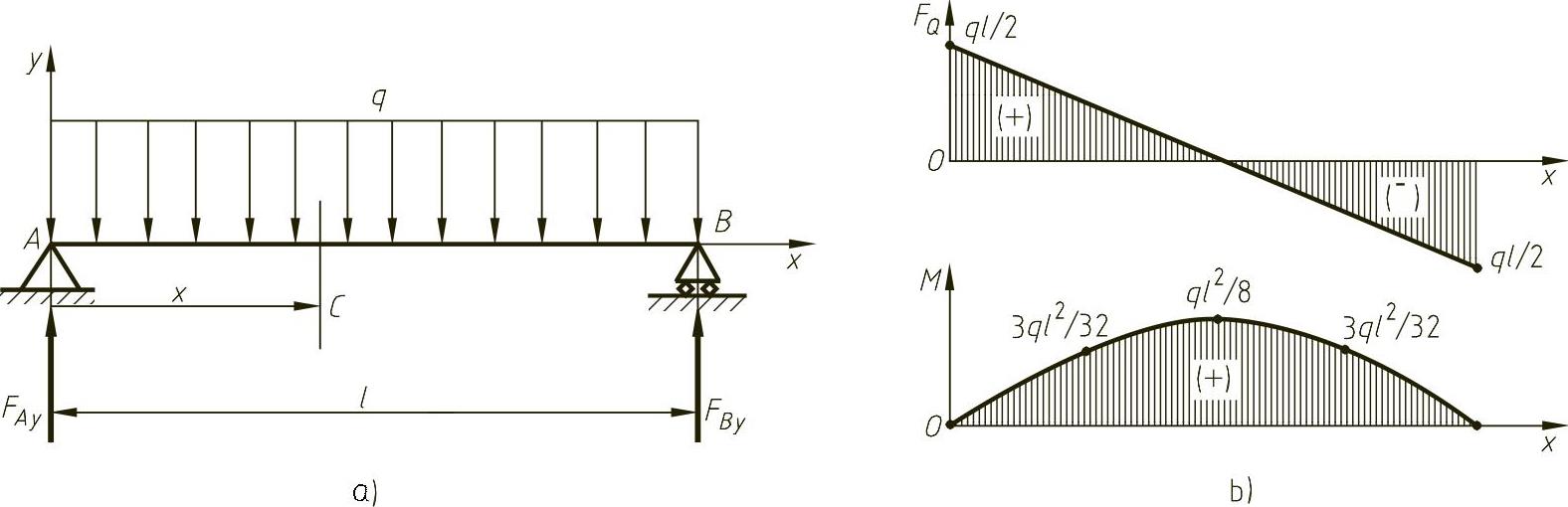
图5-11 例5-4图

解 1）确定约束力。由

∑M_A=0， ∑M_B=0

得 F_Ay=F_By=ql/2

2）写出剪力和弯矩方程

F_Q（x）=ql/2-qx （0＜x＜l）

M（x）=qlx/2-qx²/2 （0≤x≤l）

3）依方程画出剪力图和弯矩图，如图5-11b所示。

4.温度分布图

图5-12所示为单层平壁的导热模型。已知平壁厚为δ，宽度和高度比厚度大得多，两侧分别维持均匀恒定的温度t₁和t₂，材料的物性值（热导率等）为常数，无内热源。分析这些条件可看出壁内温度只沿x轴方向变化，是一维稳态导热。

此类导热问题的通解为

t=c₁x+c₂

式中，c₁和c₂为积分常数，，c₂=t₁，则可得单层平壁内的温度分布为

式（5-1）是一个线性方程，其图形是一条直线。

图5-13所示为一常物性、无内热源的单层圆筒壁的导热模型，内、外半径分别为r₁和r₂；内、外表面的温度恒定、均匀，并分别维持t₁和t₂；长度l远大于外径d₂。选用圆柱坐标，则该圆筒壁的温度分布为

t=c₁lnr+c₂

其中，，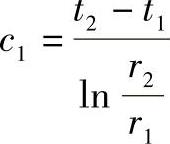

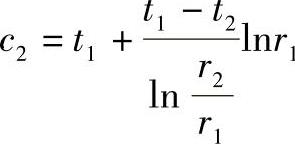
由此可得圆筒壁中的温度分布为

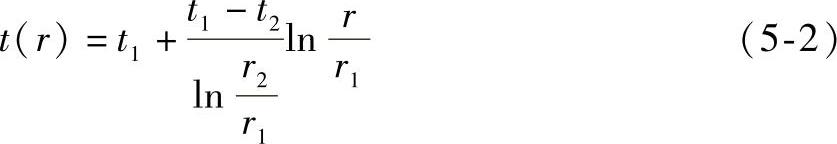
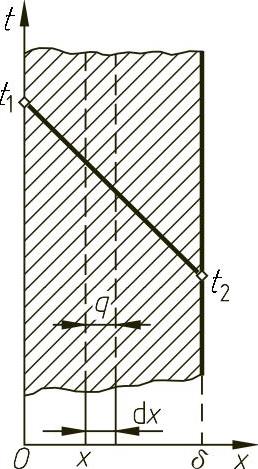
图5-12 单层平壁的导热模型

式（5-2）为对数曲线方程，其图形是一条对数曲线。

图5-14a所示为空心球的导热模型，球的内、外半径分别为r₁和r₂，内、外表面分别维持恒定均匀温度t₁和t₂，则上述球壁温度分布为

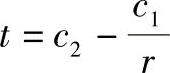
其中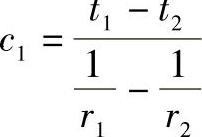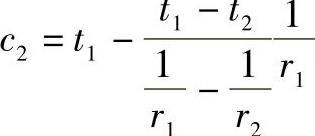，，。将c₁、c₂代入得

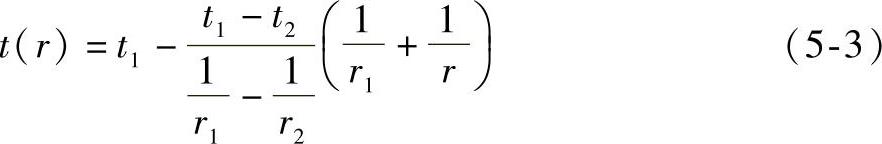
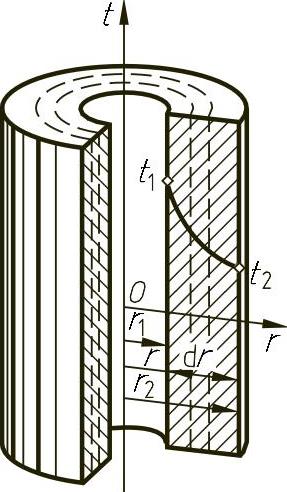
图5-13 单层圆筒壁的导热模型

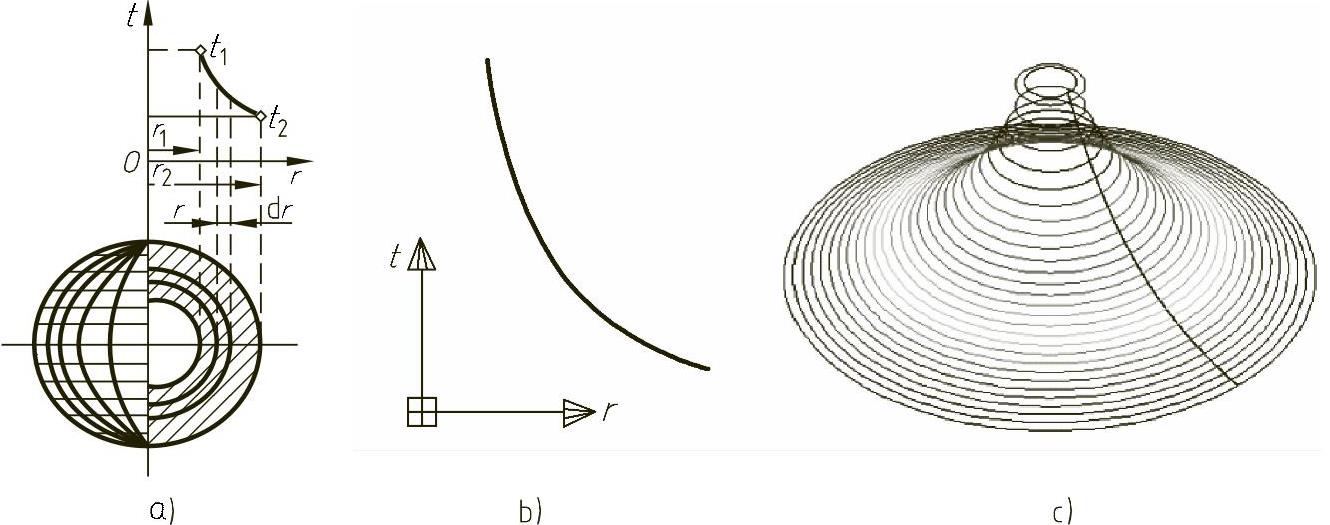
图5-14 空心球的温度分布

a）空心球的导热模型 b）温度曲线 c）温度曲面

式（5-3）为双曲线方程，其图形是一条双曲线。当空心圆球的内径为30mm、外径为130mm，内表面温度为160℃、外表面温度为10℃时，双曲线的形状如图5-14b所示。利用该双曲线绕过球心的轴旋转，可以得出一个旋转曲面，如图5-14c所示。该旋转曲面的物理含义是在上述条件下，球壳体壁上某一纬圆上点的温度值是该点所在纬圆的高度。