曲面接触点附近的几何性质详解

图4-85所示为两个任意形状的物体，当其在O点接触时，总可以在O点找到一个对两物体同时相切的公共切面。取两个坐标系Ox₁y₁z₁及Ox₂y₂z₂它们分别固联于两个物体①、②上，并将坐标原点选在O点。把x、y坐标放在公切面内，一般来说x₁轴与x₂轴并不重合。并令正向的z₁指向曲面①在O点的曲率中心，z₂的正向指向曲面②在O点的曲率中心，即z₁与z₂轴处于两物体的公法线上。

原点附近两曲面的方程可以表示为

如将函数F（x，y）按泰勒级数在O点展开，得

图4-85 两个任意物体的接触

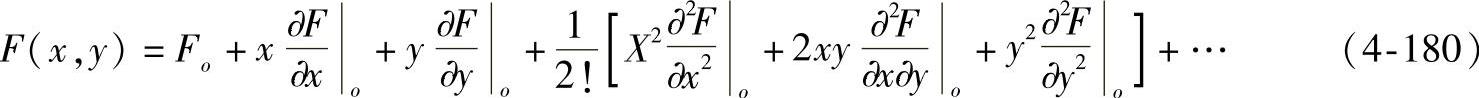
式中下标o表示函数及其各阶导数在原点（x=y=0）的值，因已将原点选在接触点，所以z_o=F_o=0又由于X、Y轴在O点的切平面内，所以

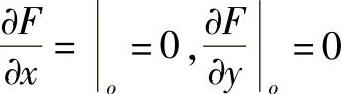
因已假设原点O不是奇异点，二次幂上各项均为零。又由于在接触问题中，接触面与整个物体的尺寸变化相比是很小的，可以只研究O点附近的曲面，为此可以把级数在三次以上的项均略去而只保留二次幂项，故得

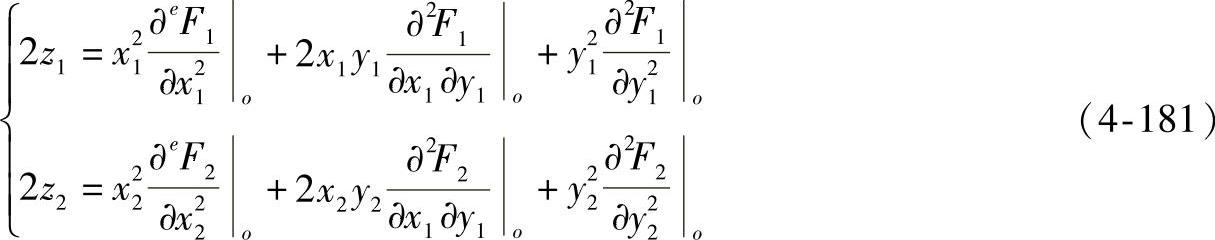
只要将x及y坐标选择到曲面在O点的主曲率上，就可以把x、y项消去，则

表示曲面与xOz相平行的平面的交线所得的平面曲线的曲率，其中xOz平面与曲线的交线在O点的曲率是一个主曲率。又由于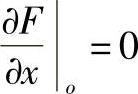，所以

式中，x₁、y₁为公切面与物体①主曲率平面的交线轴。

同时，对于物体②，以公切面与主曲率平面的交线为x₂、y₂轴，所以

k的下标中第一个表示物体号，第二个表示主曲率号。假设水平轴x、y都已转动过了，因此，过原点的两个曲面方程可以写成

一般地讲，x₁轴与x₂轴，y₁轴与y₂轴是不重复的，如图4-86所示，令x₁轴与x₂轴之间的夹角为ω，当统一研究两物体的几何关系时，用两个不同的坐标系不很方便，为此找一个共同的坐标系xOy，将式（4-184）所表示的两个微小的曲面用新坐标x、y表示，而z轴不动。如图4-86所示的新坐标系xOy，x轴与x₁轴及x₂轴之间的夹角分别为ω₁及ω₂，且有以下关系

ω=ω₁-ω₂ （4-185）

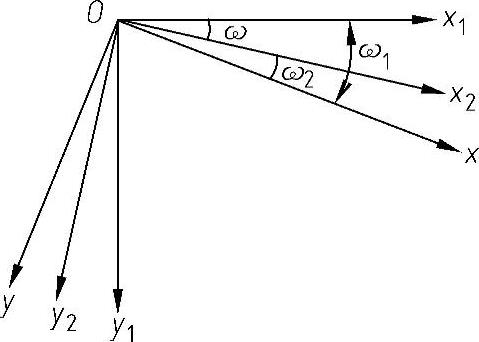
图4-86 坐标系变换

应用坐标转轴的变换公式得

将上式代入曲面方程可得

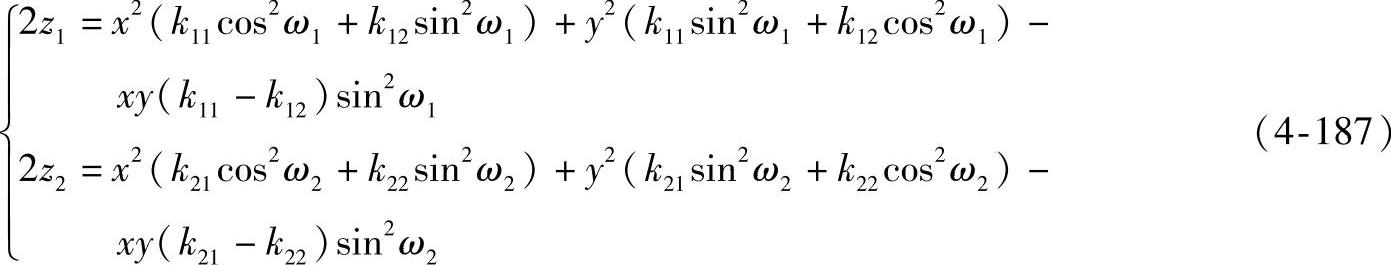
把以上两式相加，可得这两曲面上有相同的x、y值的两点（M，N）间距离为z₁+z₂，得

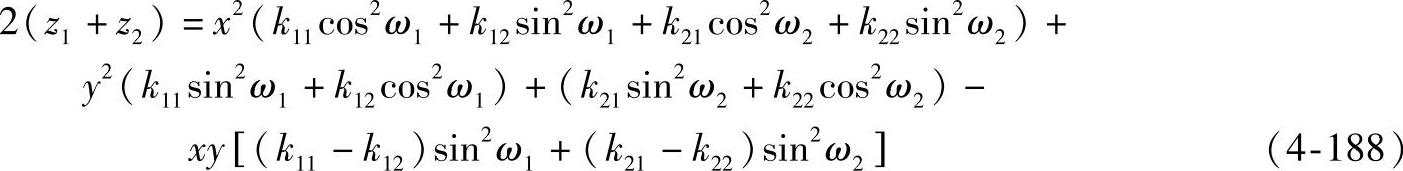
现再次转轴以选择合适的ω₁及ω₂，使上式中的x、y项消失，即

（k₁₁-k₁₂）sin²ω₁+（k₂₁-k₂₂）sin²ω₂=0 （4-189）(www.xing528.com)

考虑到ω₁=ω₂+ω及ω₂=ω₁-ω，分别代入上式得

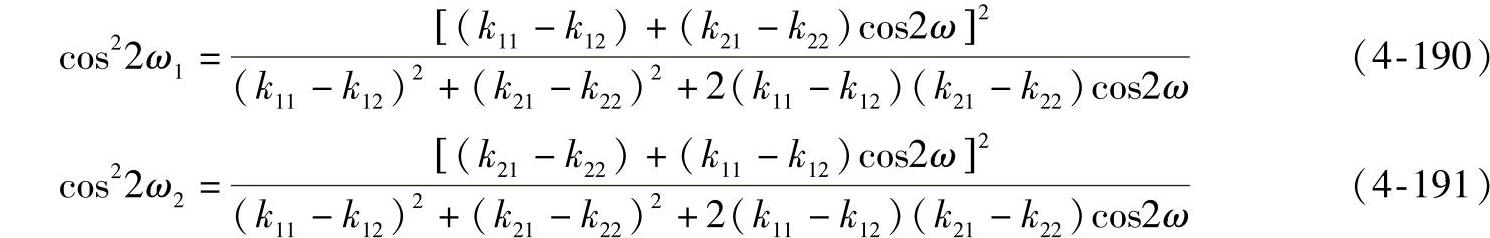
如将以前式中x²与y²项之前的系数表示为

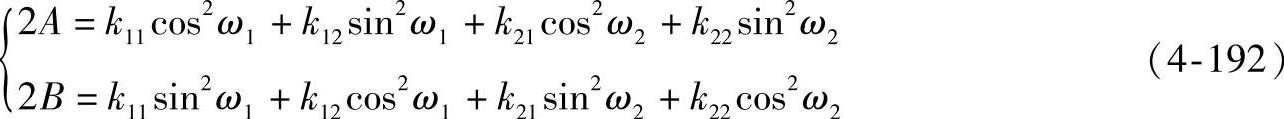
则得

z₁+z₂=Ax²+by² （4-193）

由几何关系可知

z₁+z₂=C （4-194）

则得

Az²+By²=C （4-195）

此式为等高线方程，该方程为一椭圆，这是因为如设A＜0，则当y=0时，沿x轴各处将出现z₁+z₂＜0的情况，这是不可能的，所以A＞0；同理可得B＞0，所以以上方程为一椭圆；取不同的C，得一相似的椭圆族。

将式（4-192）中两式先相加，后相减，得

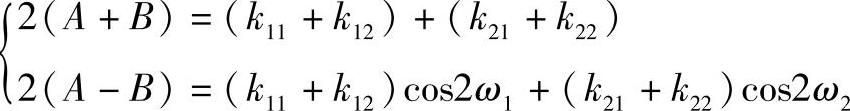
将式（4-190）、式（4-191）代入上式，可将A、B表达成

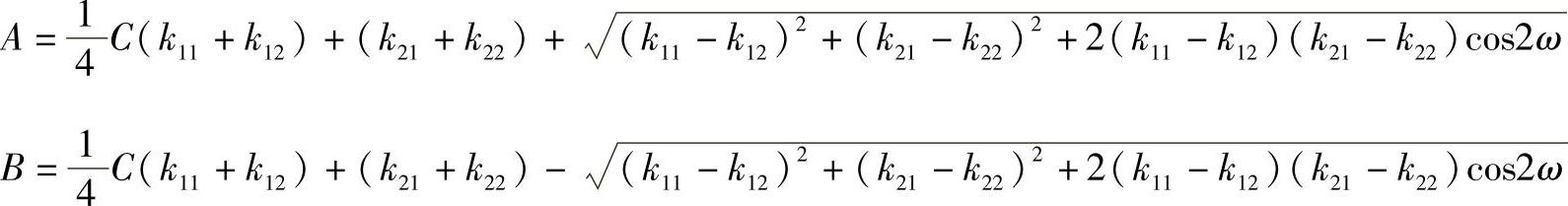
式中，ω为k₁₁和k₁₂之间的夹角。

当规定x轴是椭圆的长轴方向时，则A＜B，将上式中计算出的值取其较小的一个作为A，而另一个较大的作为B。

虽然上式比较烦琐，但由于在工程实际问题中，接触物体的几何形状一般比较规则，计算并不复杂，现举例如下：

例4-28 半径为R₁与R₂两圆球接触时，如图4-87所示。由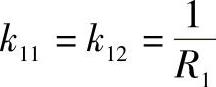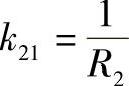，，k₂₂=0，夹角ω可为任意值可得A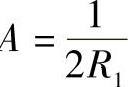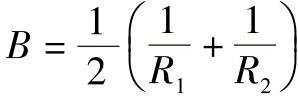，，接触面为圆。

例4-29 半径为R₁的圆球与半径为R₂的圆柱体接触时，如图4-88所示。

由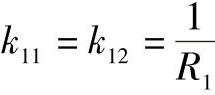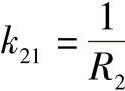，，k₂₂=0，夹角ω可为任意值可得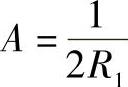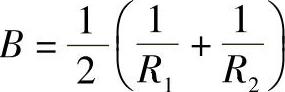，，接触面为椭圆。

例4-30 轴线互相垂直，半径为R₁、R₂的两圆柱体接触，如图4-89所示。

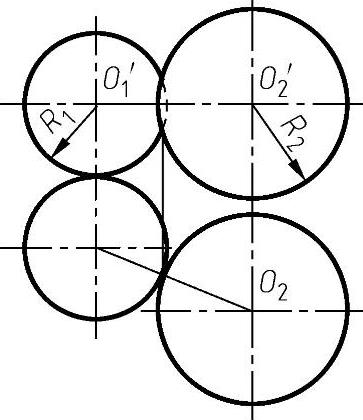
图4-87 两球面接触

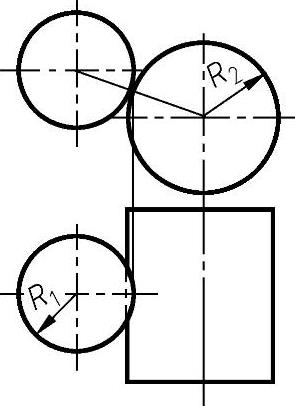
图4-88 球面与圆柱面接触

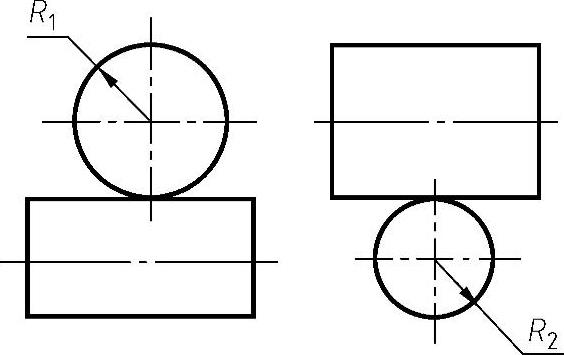
图4-89 两圆柱面接触

由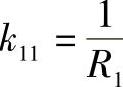，k₁₂=0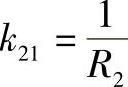，，k₂₂=0，夹角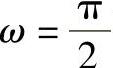可得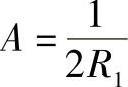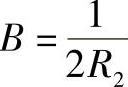，。当R₁=R₂时接触面为圆；当R₁=∞时，平面与圆柱接触的接触面为平行两直线间的面积；一般情况接触面为椭圆。