曲面梯度的基本分量实验

由曲面上I点偏导数的定义可知，确定曲面的梯度的基本分量可以转化为用图形求解迹线所表示的切平面。

1.圆锥面基本梯度分量

由图4-78可得

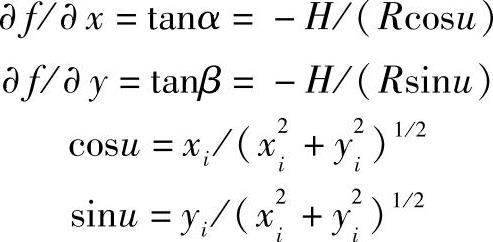
2.球面基本梯度分量

由图4-79可得

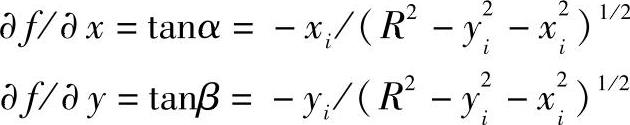
3.圆环基本梯度分量

由图4-80可得

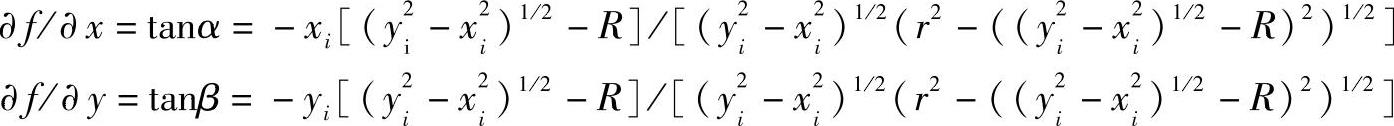
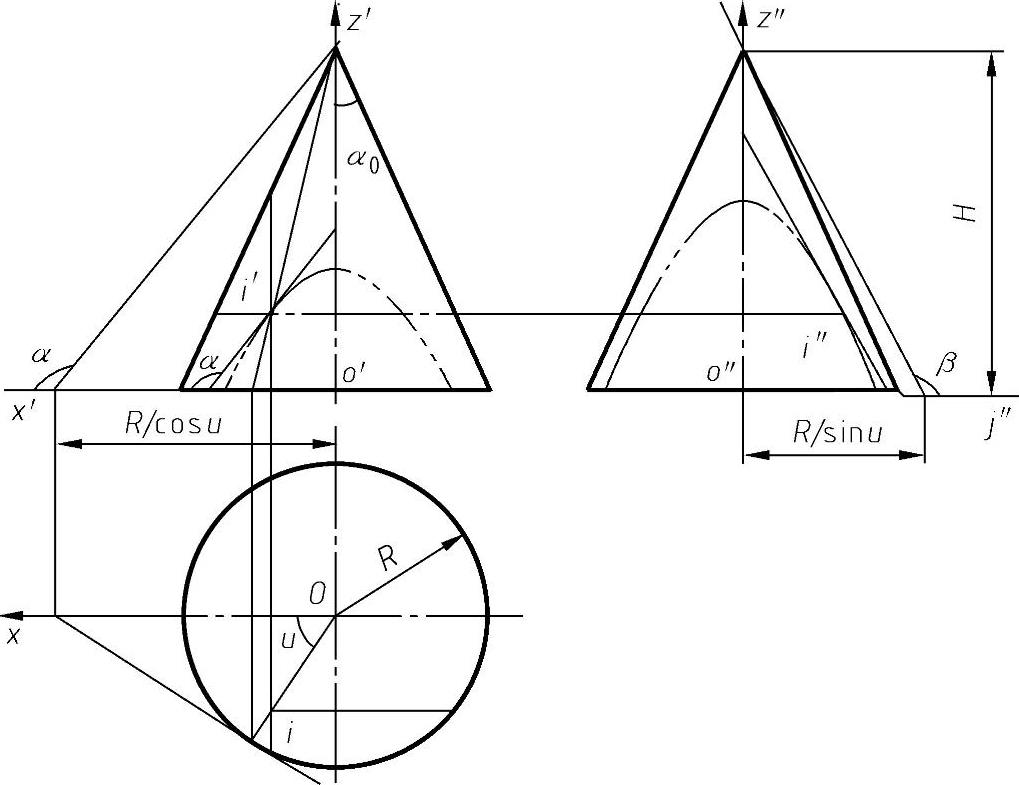
图4-78 圆锥面基本梯度分量

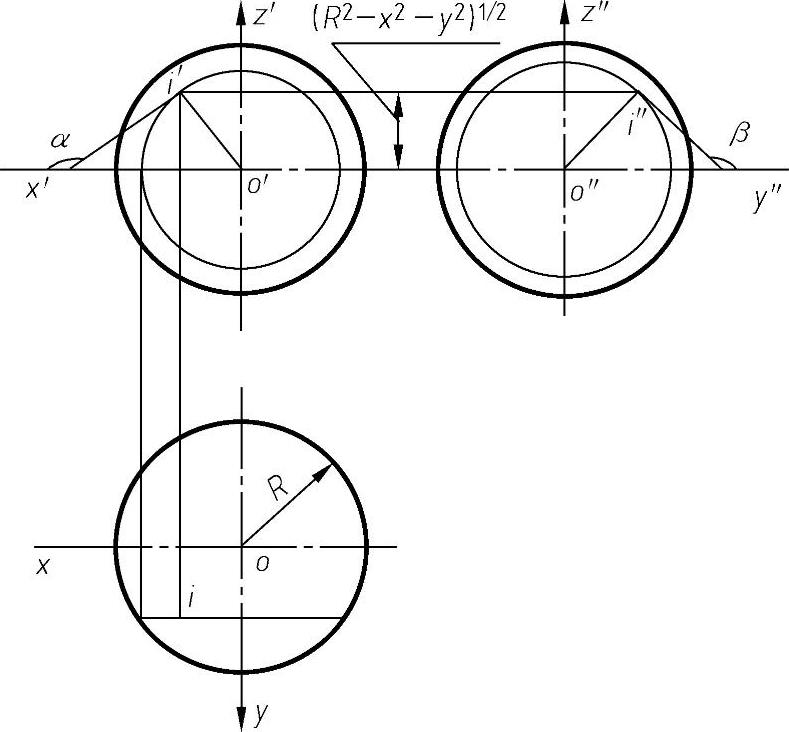
图4-79 球面基本梯度分量

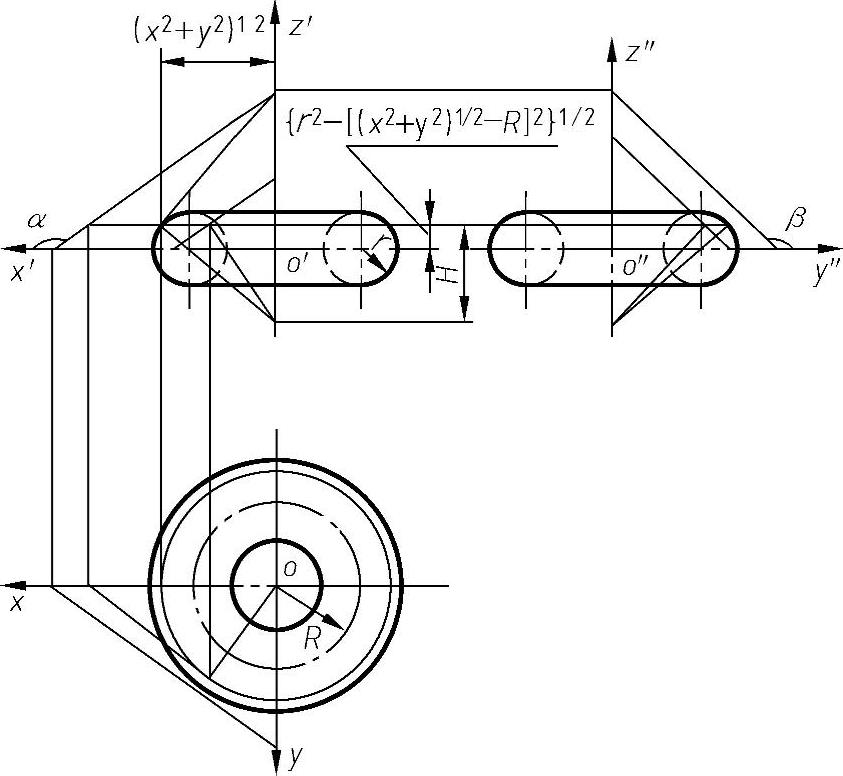
图4-80 圆环基本梯度分量

4.抛物面梯度的求解

（1）抛物面梯度的数学表达 设抛物面的方程为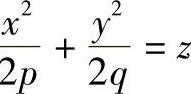（当p=q＞0方程为旋转抛物面，当p≠q＞0方程为椭圆抛物面，当p＞0、q＜0方程为双曲抛物面）。

根据梯度的定义，抛物面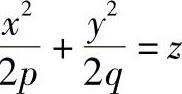的梯度可以表示为

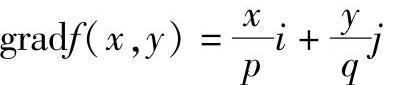
将已知点P_a（x_a，y_a，z_a）代入，可以求得抛物面上该点处的梯度为

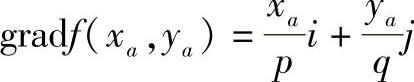
设P_a（x_a，y_a，z_a）点变化最快的路径参数方程为x=x（s），y=y（s），而曲面上任意一点的切向量为{x′（s），y′（s）}，令x′（s）=x（s），y′（s）=y（s），解微分方程得(https://www.xing528.com)

x（s）=c₁e^s，y（s）=c₂e^s

代入已知条件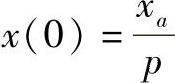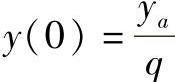，，即可得到P_a（x_a，y_a，z_a）点处变化最快路径为

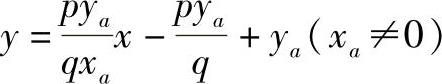
（2）抛物面上一点处切平面的几何作图 当用y=y_a或x=x_a平面截切抛物面时，其截面轮廓是一抛物线。为了方便作图，以旋转抛物面为例说明作图过程，对于椭圆抛物面和双曲抛物面其作图过程也是相同的。设P_a（x_a，y_a，z_a）为抛物面上一点，当x_a、y_a不同为0时，用y=y_a的平面截切旋转抛物面，则可以得到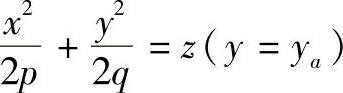的抛物线，如图4-81所示。其顶点为O₁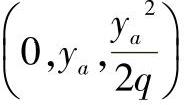，过O₁作与x轴平行的直线x₁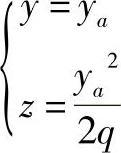，，由点p_a向x₁作垂线，垂足为M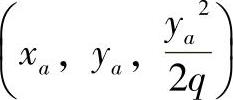，线段O₁M的中点为Q₁。

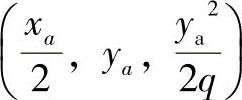同样，用x=x_a的平面截切抛物面，则可以得到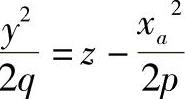的抛物线，其顶点为O₂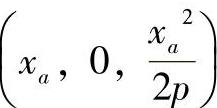，过O₂作与y轴平行的直线y₁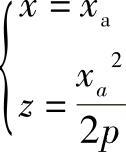，，由点p_a向y₁作垂线，垂足为N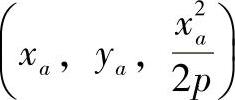，线段O₁N的中点为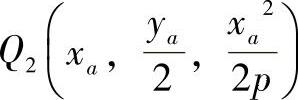。则由Q₁p_a和Q₂p_a确定的平面即为抛物面上p_a点处的切平面。

（3）抛物面上梯度的图解 根据梯度的图解原理知道它是最大斜度线对H面倾角的正切。求解曲面上某点梯度需求出该点切平面对H面的最大斜度线。因切平面对H面的最大斜度线垂直于该面内水平线。按照这个定义可以作出旋转抛物面上P_a（x_a，y_a，z_a）点处的切平面的最大斜度线，如图4-82所示。

先作水平线Q₁M。过q′₁作q′₁m′平行于x轴，根据已知条件求得m′点x、z坐标为x_a、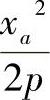。利用画法几何原理作图得到M点的H面投影m。它的y坐标可以根据其所在的切平面的方程求出。抛物面在p_a点处切平面的法向量为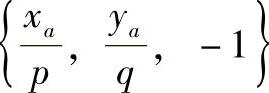，利用点法式求出其切平面方程为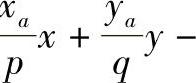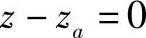，将x_a、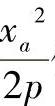代入求得y坐标为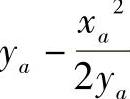。至此，可得到点。

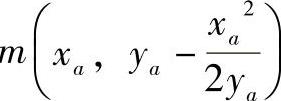现过p_a（x_a，y_a）作垂直于q₁m的直线Op_a。Op_a就是p_a点处的最大斜度线的水平投影线。因q₁m所在直线的斜率k为

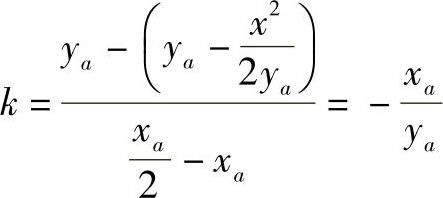
最大斜度线水平投影直线方程为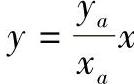。同时它也是该点变化最快的方向，即梯度方向。同理，根据图4-83可以得到椭圆抛物面在p_a点的梯度方向为

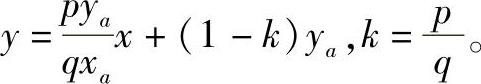
在图4-84中，双曲抛物面在该点的梯度方向为

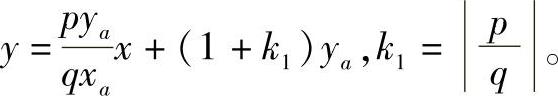
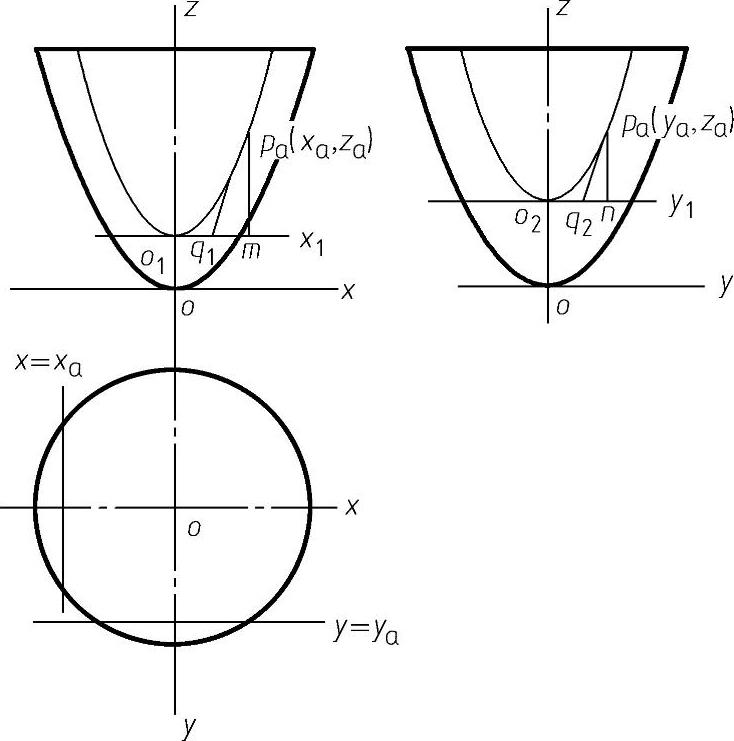
图4-81 正平面截切抛物面

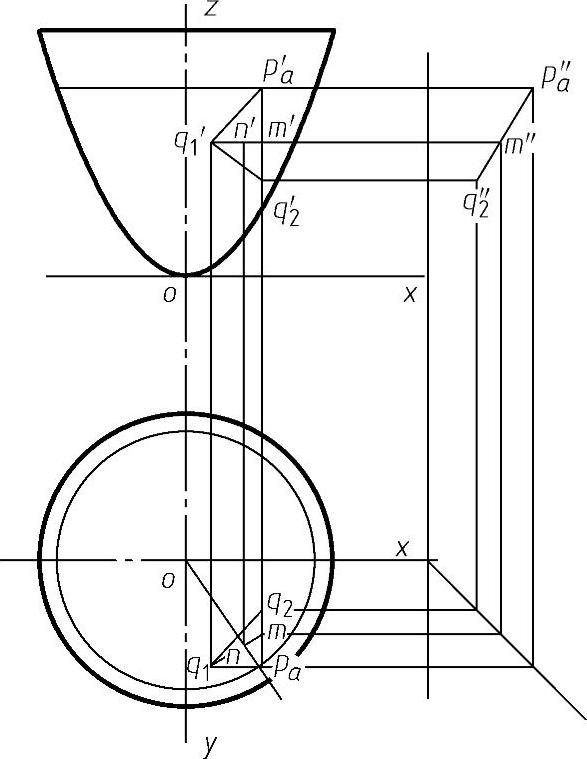
图4-82 旋转抛物面梯度图解

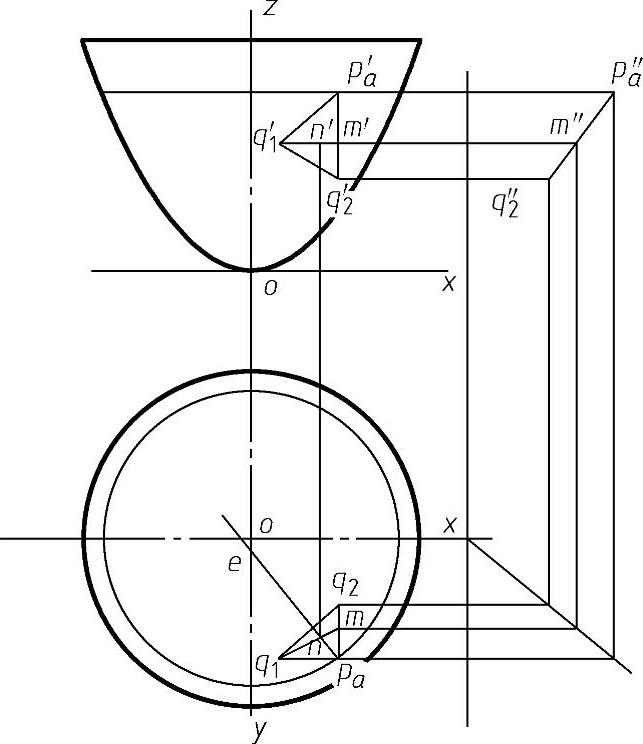
图4-83 椭圆抛物面梯度图解

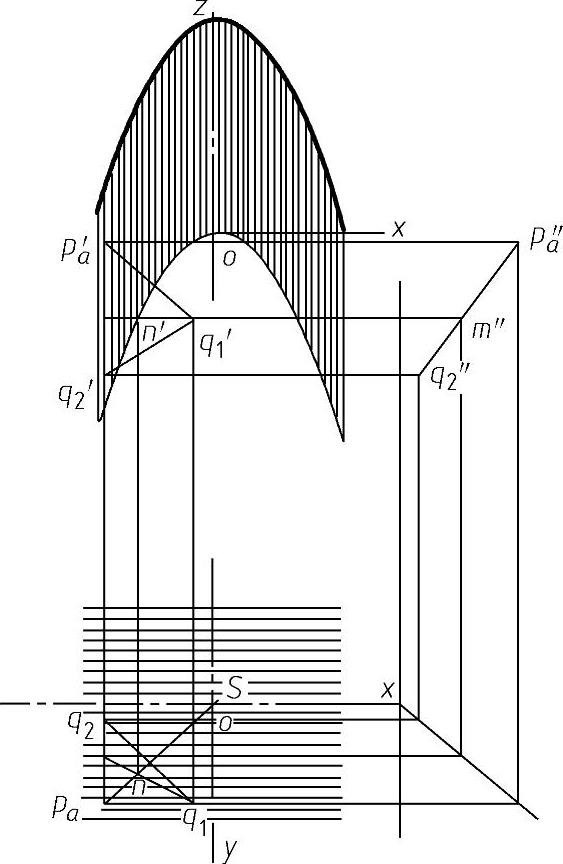
图4-84 双曲抛物面梯度图解