曲面上的测地线计算-计算机实验工程图形学.下册

就局部性质而言，测地线是短程线即曲面上两点之间的最短距离线，其作用相当于平面上的直线。在对某些问题的研究中会应用到测地线。例如，假设一质点在曲面上自由运动，如无外力，则质点在曲面上的运动轨迹就是短程线；一条无质量的弹性细线在一光滑曲面上自由移动，当这条细线在曲面上两点间的张力作用下而处于平衡状态时，其形状也是测地线等。

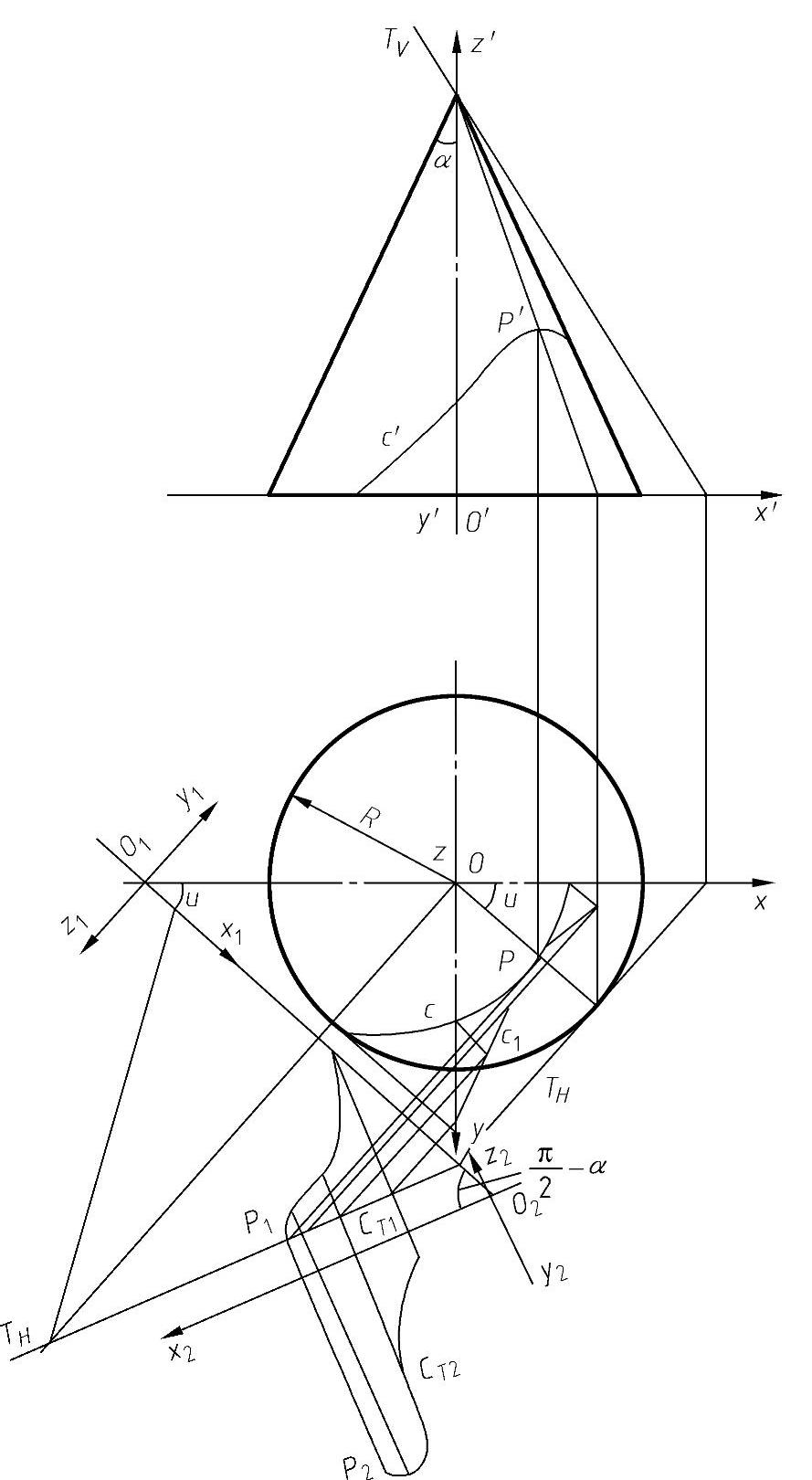
图4-72 圆锥面曲线上点的测地曲率

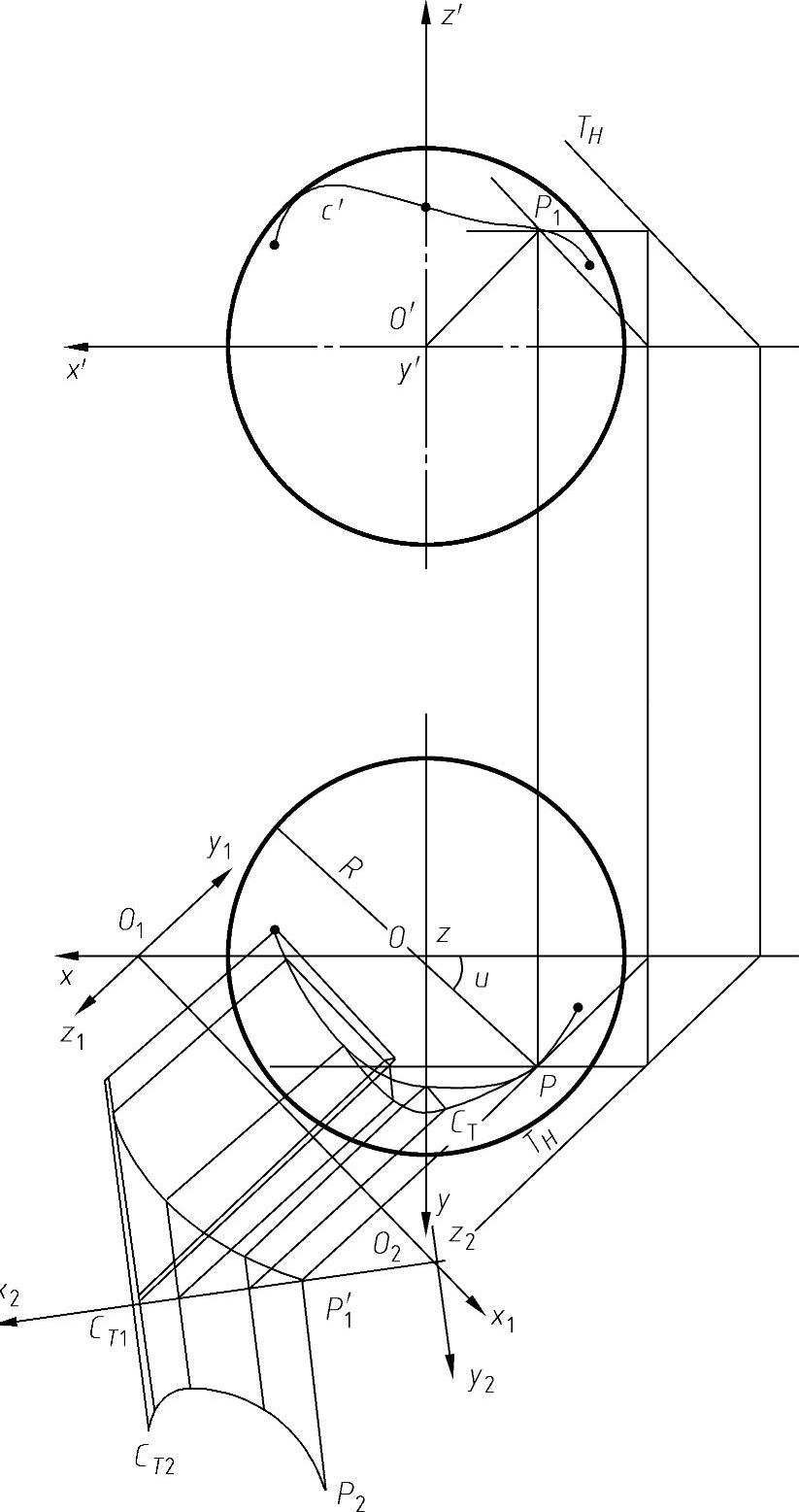
图4-73 圆球面曲线上点的测地曲率

1.测地线的数学解

测地线在正交网中的微分方程可以写作

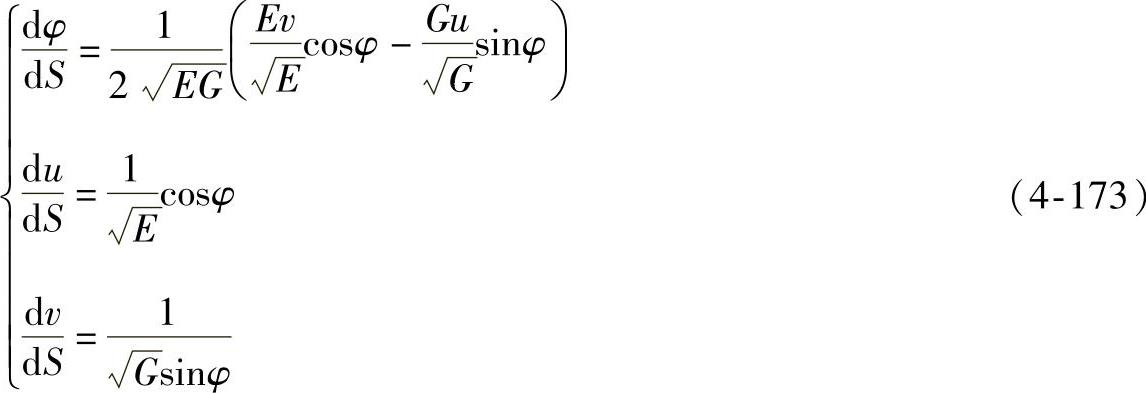
式（4-173）也可以写成

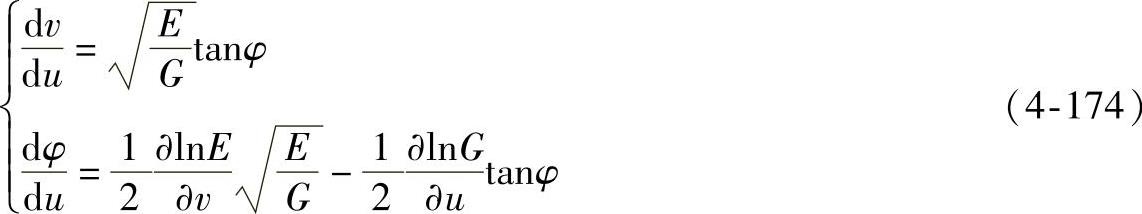
这个方程组是由三个变量u、v、φ及自变量S构成的，解此方程组可以确定测地线的参数方程。因u、v、φ有连续偏导数，对已给的初始条件

就有唯一解

例4-22 已知圆锥面方程为

r={usinαcosv，usinαsinv，ucosα}

求圆锥面上的测地线方程。

解 由第一基本量

E=r_u·r_u，F=r_u·r_v，G=r_v·r_v

得E=1，F=0，G=u²sin²α

由式（4-174）得

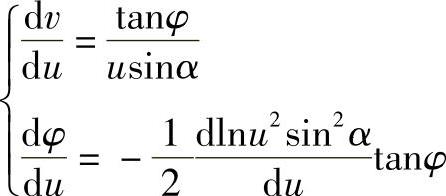
于是有

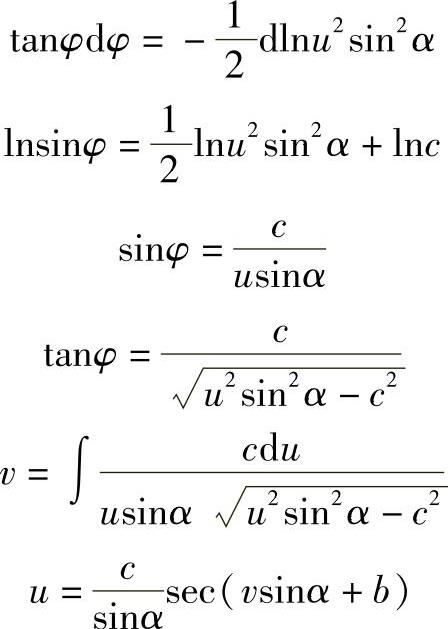
式中，c、b均为积分常数。

在求圆锥面上连A、B两点的测地线时，由A、B两点坐标可定出c、b常数。

由A、B两点坐标可得

u=u_A，v=v_A

u=u_B，v=v_B

故有

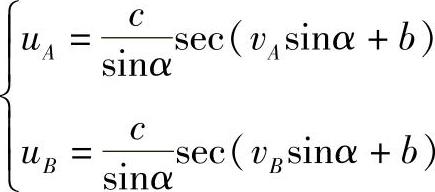
解出

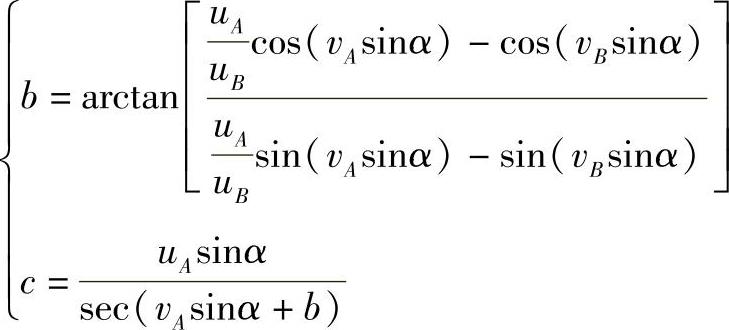
至此可得圆锥面上连A、B两点的测地线方程为

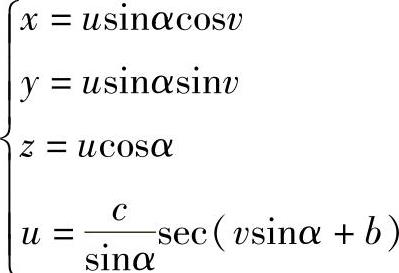
例4-23 设圆锥半径R=20mm，高H=30mm，圆锥面上A、B两点的坐标为

x_a=10，y_a=17.320508，z_a=0

x_b=-6.6666667，y_b=0，z_b=20

求连接A、B两点的测地线上某点I的坐标，已知z_i=9.999206。

解 先根据已知条件算出

b=76.139509°，c=-6.650308

再由z_i算出对应的u值为u=24.037365，而v=78.923469，由此得I点的坐标为

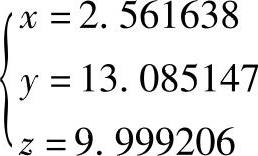
例4-24 已知圆柱面方程为

r={Rcosv，Rsinv，u}

求圆柱面上的测地线方程。

解 圆柱面第一基本量E=1，F=0，G=R²，由式（4-174）得

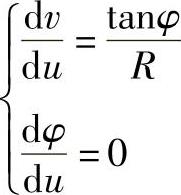
于是有

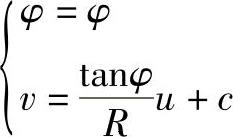
式中，φ、c为积分常数。

设A、B为测地线上两点，当A、B两点为已知时，由此两点坐标可得

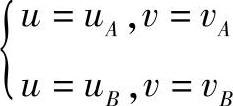
由此可得

因而圆柱面上连接A、B两点的测地线方程为

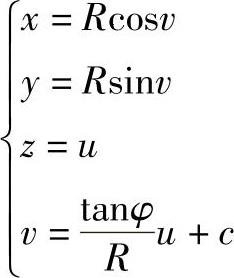
例4-25 设圆柱面半径R=50，圆柱面上A、B两点的坐标为

x_a=43.30127，y_a=25，z_a=0

x_b=-50，y_b=0，z_b=60

求连接A、B两点的测地线上某点I的坐标，已知z_i=30。

解 先根据已知条件算出φ=89.541644°，c=30，再由z_i=30算出v=105，由此得

x=-12.940953，y=48.296292，z=30

例4-26 设A（x₀，y₀，z₀）、B（x₁，y₁，z₁）是球面x²+y²+z²=a²上的两点，在球面上求作连接A、B两点的测地线。

解 设曲线表示为

y=y（x），z=z（x），x∈[x₀，x₁]

它的弧长是

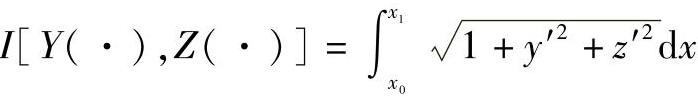
求测地线即是求曲线使泛函为最小。为此，构造一个辅助泛函

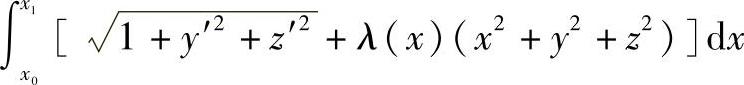
它对应的欧拉方程组是

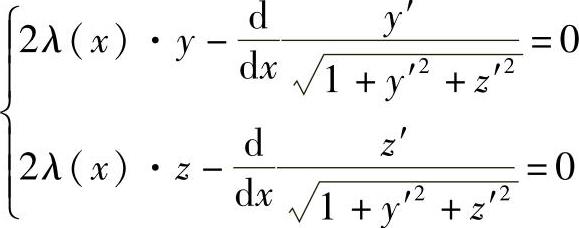
解这些常微分方程，得到依赖于四个常数的曲线族。由条件y（x₀）=y₀，y（x₁）=y₁，z（x₀）=z₀，z（x₁）=z₁确定这些常数，得到要求的测地线是过点A、B的大圆弧的劣弧段。这个问题也可利用球面坐标，把它化为参数方程，变成无条件的变分问题来求解。令

x=asinθcosφ，y=asinθsinφ，z=acosθ

此时球面上的弧元

dS²=a²（dθ²+sin²θdφ²）

把θ看做是独立变量，φ看做是θ的函数，于是测地线应使

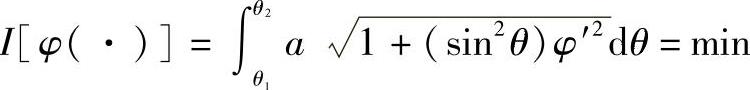
因为上式被积函数中不含φ，故其欧拉方程有初次积分

F_φ′=c₁

即

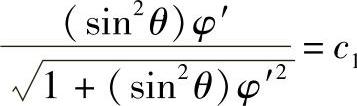
从上式解出φ′，可以得到

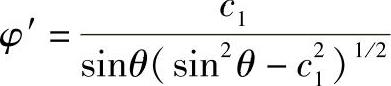(www.xing528.com)

显然从前述关系可知|c₁|≪1，于是令c₁=sinα代入上式得

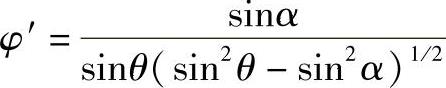
积分得

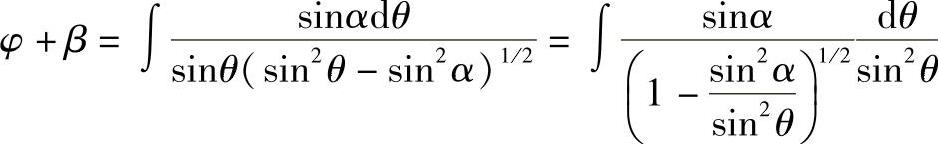
再令

ctanθ=u

则

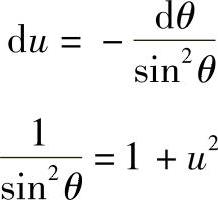
于是有

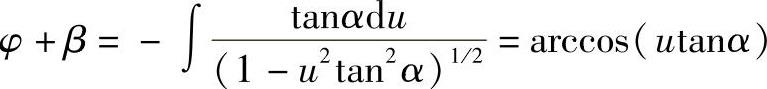
即有 cos（φ+β）=tanα（ctanθ）

或写成

sinθcosφcosβ-sinθsinφsinβ=tanαcosθ

换回到x、y、z为

xcosβ-ysinβ-ztanα=0

这就是过原点的平面，它与球面的交线即为所求。

2.测地线的形数结合解

上述求解测地线的方法比较抽象，当用画法几何方法图示图解曲面上的测地线时，问题就比较直观。在此基础上再建立求解测地线的数学模型，这样就可使问题既具体、直观又有精确性，且不失一般性。

图4-74所示为正圆锥面的两面投影，已知A（a，a′）、B（b，b′）为圆锥面上的两点，求A、B两点的测地线。

由平面几何知，平面上两点间的最短距离为连接此两点的直线段。故先将圆锥展开为平面，并在展开图上定出A、B两点的位置A₀、B0（根据圆锥展开方法来确定）。连接A₀、B₀两点得直线段A₀B₀，即完成测地线长度的图解。因A₀B₀上的点与圆锥面上连接A、B两点的测地线上的点有一一对应关系，因此只要求出A₀B₀线上各点在圆锥面上的对应点，即可得到测地线的投影。此为图解方法，为了建立此测地线的方程，在图中建立坐标系Oxyz，在所设坐标系中展开图上直线A₀B₀上某点I₀的坐标为

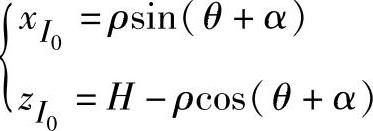
式中各量如图4-74中所示，其中

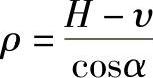
由此得

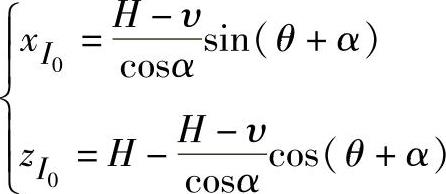
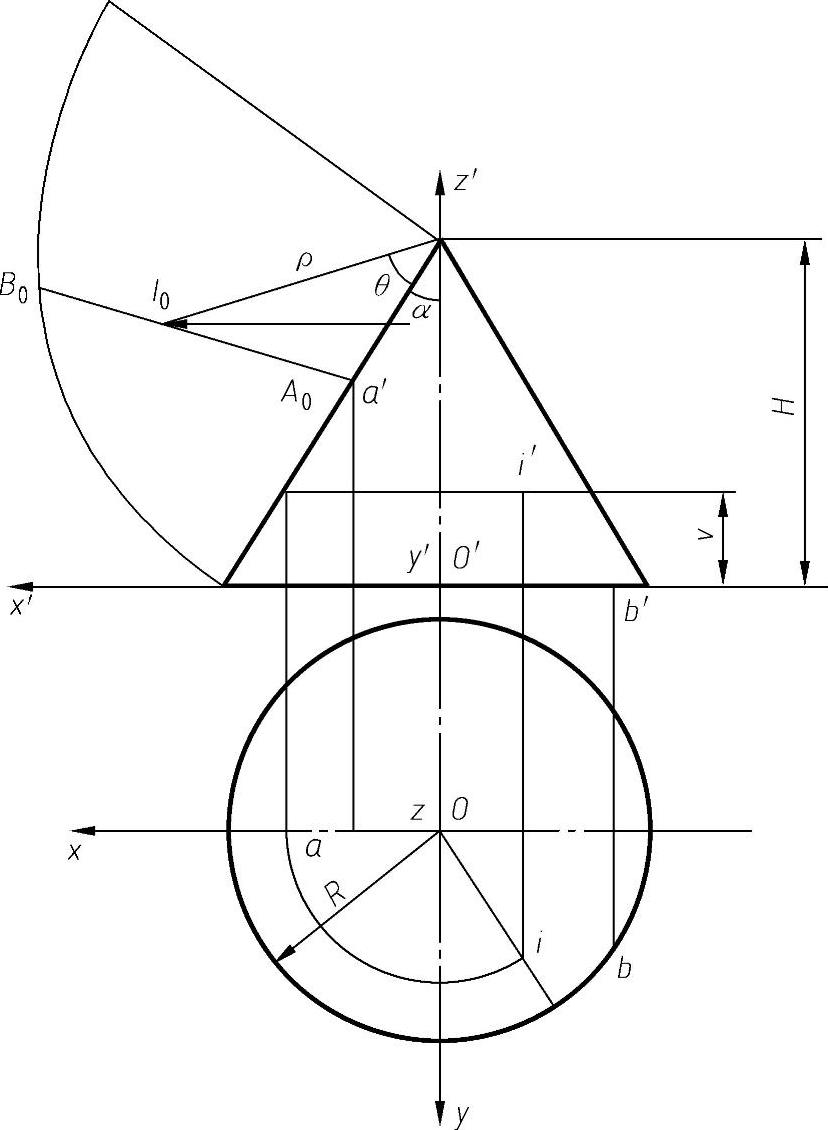
图4-74 圆锥面上的测地线

A₀、B₀点的坐标为

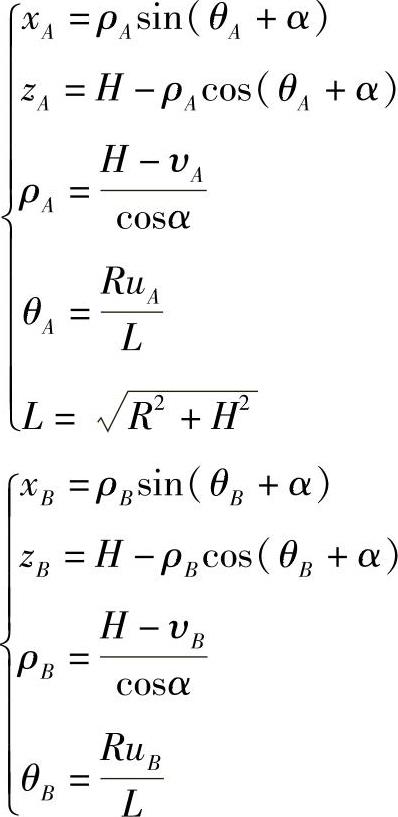
A₀B₀方程为

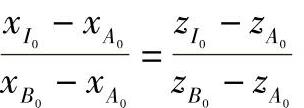
将前述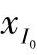、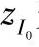关系代入上式得

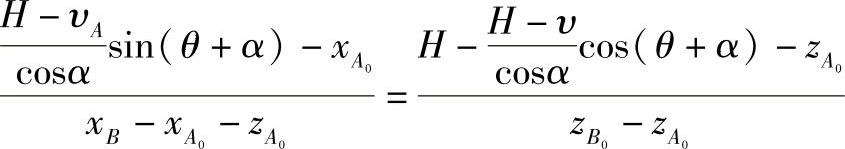
令

则有

Asinβ+Bcosβ=E

解出

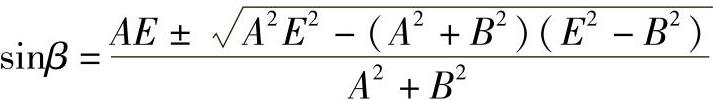
而

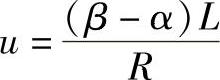
于是I₀点在锥面上的对应点I的坐标为

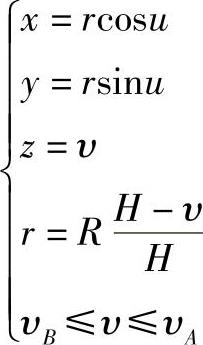
当I₀点在A₀B₀直线上变动时，即可得各对应点I的坐标，因此上式实质上就是圆锥面上连接A、B两点的测地线方程。

例4-27 设圆锥底圆半径R=20mm，锥高H=30mm，A、B两点的坐标为x_a=10，y_a=17.320508，z_a=0，x_b=-6.6666667，y_b=0，z_b=20，求连接A、B两点的测地线上高为z_I=

9.999206的点I的x、y坐标。

解 将已知条件代入上述各有关公式，分别算出A、B、E值，然后算出β值，再算出u=78.923427°，r=13.333529，即可算出I点的坐标为x=2.5616472，y=13.085143，z=9.999206。

图4-75a所示为椭圆柱面的两个投影，已知A（a，a′）、B（b，b′）为椭圆柱面上两点，求连接A、B两点的测地线。

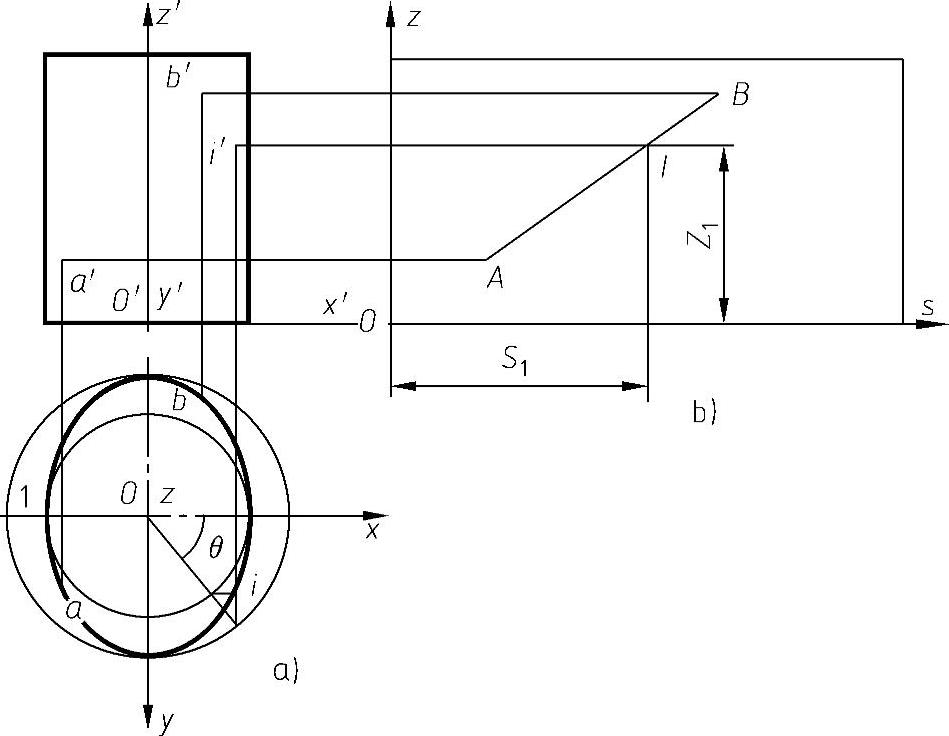
图4-75 椭圆柱面上的测地线

图4-75b所示为椭圆柱面展开图，在展开图上定出A、B两点的位置后可得直线AB，完成测地线长度的图解。直线AB上的点与椭圆柱面上连接A、B两点的测地线上的点相对应。

因此，只需求出直线AB上各点的对应点即可求得测地线的投影，其作图方法如下：

1）在直线AB上任取I点，I点的z坐标与其在椭圆柱面上对应点的z坐标相同。故知i′必在过I点所作的OS轴的平行线上。

2）在H投影面上，展开图中的S₁长度从x轴与椭圆的交点I开始度量到椭圆上，使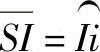。i为I点对应点的水平投影。

3）由i点引投影线与由I所作的轴的平行线相交得i′，i′为I点对应点的正面投影。

依次作图，在直线AB上取一系列点并求出它们在椭圆柱面上的对应点，然后用曲线依次光滑相连各点，即完成测地线的投影。

在展开图上，以矩形两边为轴建立坐标系sOz，如图4-75b所示。在此坐标系中直线AB方程为

z₁=KS_I+D

当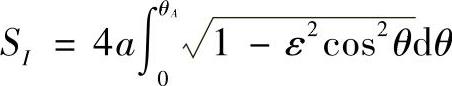时，z₁=z_A，其中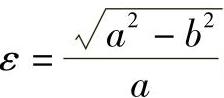，；a、b为椭圆长、短半轴。

当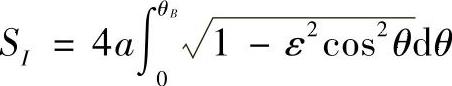时，z_I=z_B，所以有，。

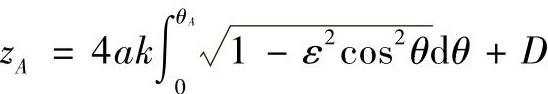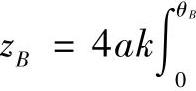
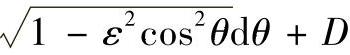由此可得

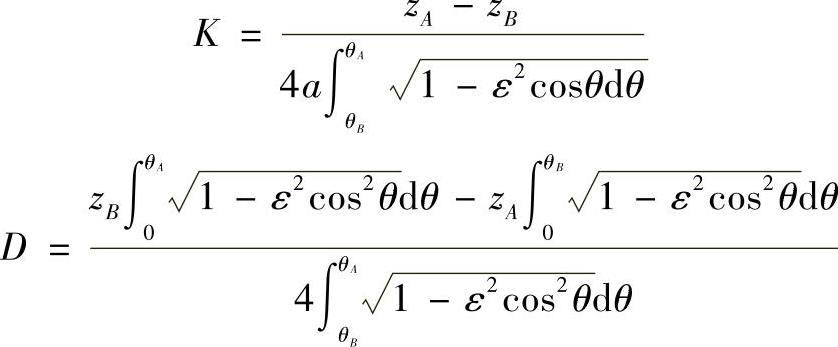
将K、D代入直线AB方程得

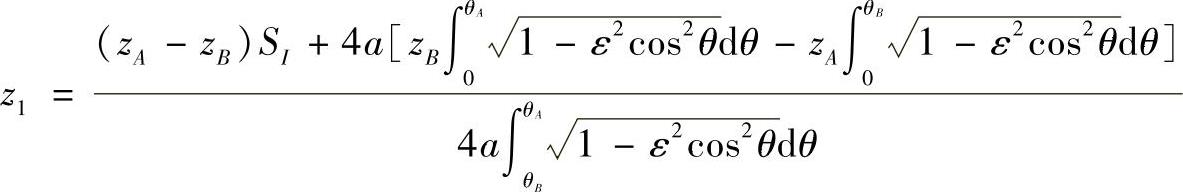
由图4-75可知，直线AB与测地线上各点的关系为

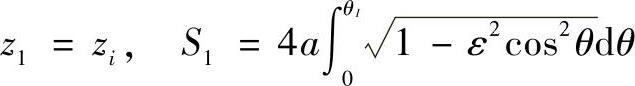
将此关系代入上式，并考虑测地线点的x、y坐标可得

此式就是椭圆柱面上连接A、B两点的测地线方程。若要求圆柱面上连接A、B两点的测地线，其与求椭圆柱面上的测地线相似，只需注意圆弧长与角度θ_i有更简单的关系，即

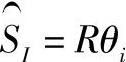
可得圆柱面上连接A、B两点的测地线方程为

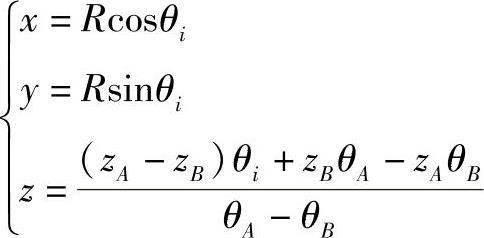
这是一条螺旋线，其作图略。

由于球面是不可展曲面，因此不能像锥、柱那样利用展开图来求测地线，但经空间反演变换，可将过反演极的球面反演成一平面。该平面平行于已知球面在极点的切平面。球面上的大圆反演成该平面上的直线。据此可知，球面上的测地线是大圆，因而连接A、B两点的测地线可按以下方法求作，如图4-76所示。

1）将A、B分别与球心O相连得OA、OB两直线，OA、OB两直线构成平面△AOB。

2）用换面法将平面△AOB变换成垂直面，球也随之。

3）在新投影体系里求出△AOB与球面的交线，即大圆，A、B两点定在交线圆上。

4）第二次投影变换求得交线实形，在交线上连接A、B两点较短的那段圆弧即为测地线实长，将此线上各点的投影返回到原投影体系中即得测地线的投影。

以球心为原点建立直角坐标系，设A、B两点的坐标分别为A（x_a，y_a，z_a）、B（x_b，y_b，z_b），测地线为过O、A、B三点的平面与球面的交线，其方程为

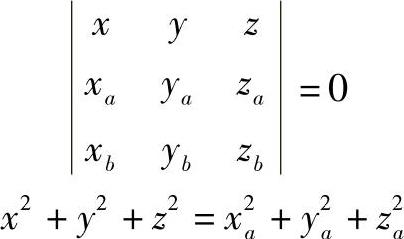
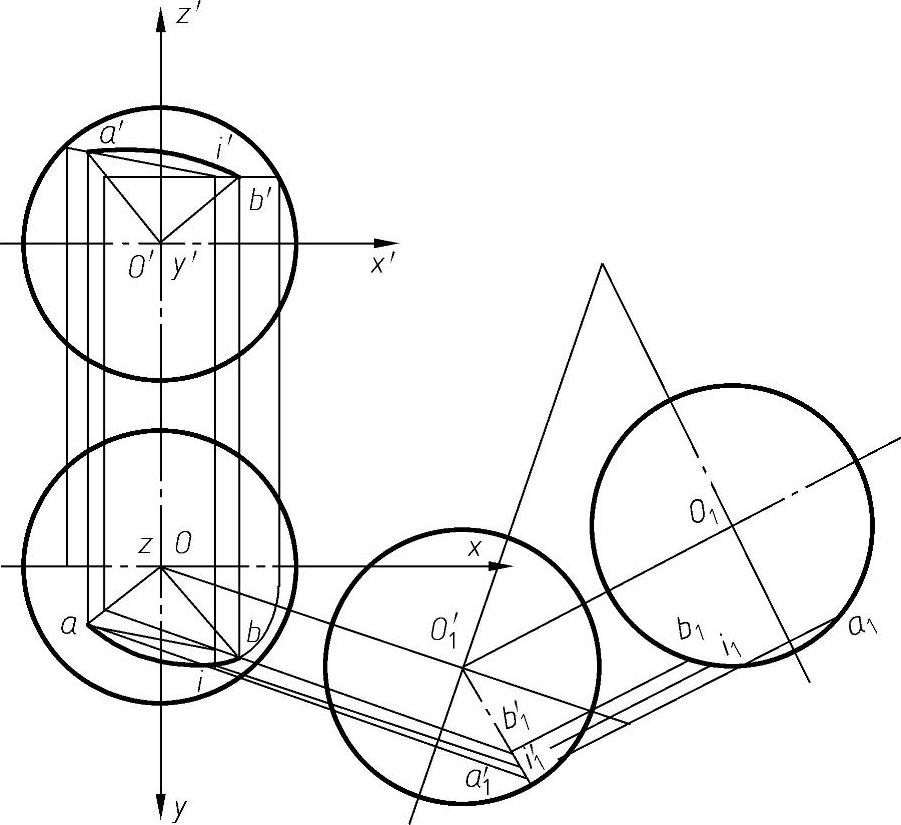
图4-76 球面上的测地线