计算机实验工程图形学-曲面曲线的曲率

曲面曲线C一般是一条空间曲线，C上点P的曲率半径位于密切平面π上，也在P点的主法线β上。π平面与C所在曲面∑相交于一条平面曲线C_π，P点在Cπ上的曲率半径与其在C上的曲率半径相同。另外，由梅尼埃定理：曲面曲线C在给定点P的曲率中心就是与C具有共同切线的法截线C₀在同一点P的曲率中心在C的密切平面上的投影。此定理中的法截线是曲面∑在P点的法线与曲线C在P点的切线所构成的法平面Q_N与∑的交线C_N。由上述可知，空间曲线C的曲率问题可转化为平面曲线的曲率来讨论。

设平面Q_N与平面π的夹角为φ，P点在C_N上的曲率半径为R_N，如图4-69所示，则P点在C_π上的曲率半径也即其在C上的曲率半径R与φ、R_N的关系为

R=R_Ncosφ （4-163）

如圆柱螺旋线上任意点I的曲率半径为R，由图4-70可知，I点处的密切平面π与法截面重合，即φ=0，故只需求出平面π与圆柱面交线在I点处的曲率半径即可。

设I点在所设坐标系中的坐标为

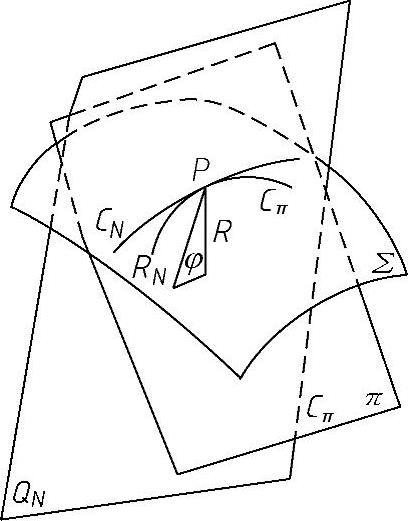
图4-69 曲面曲线的曲率

则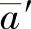（圆柱螺旋线正面投影上过i′点的切线）方程为

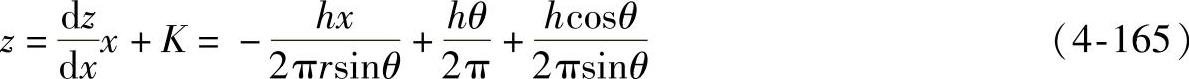
a（圆柱螺旋线水平投影上过i点的切线）方程为

由此可得N点坐标为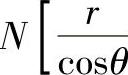，0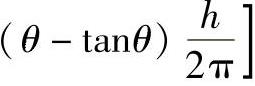，，迹线π_V过N、O₁点，O₁点坐标为O1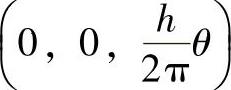，由N、O₁两点即可得π_V的方程并可得π_V与X轴的交点π_x的坐标为πx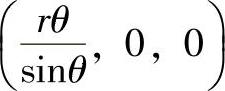，于是有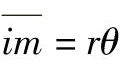，在△i₁′im中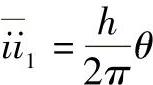，，故有

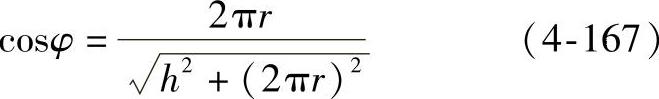
由此可得平面π与圆柱面交线椭圆的长、短半轴为(www.xing528.com)

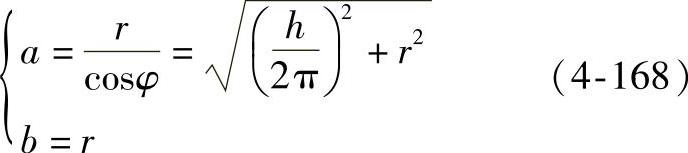
设截交线椭圆在x₂O₂y₂坐标系中的方程为

则x、y对t的一阶、二阶导数分别为

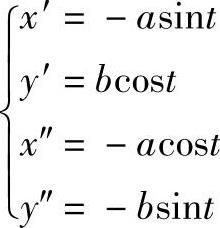
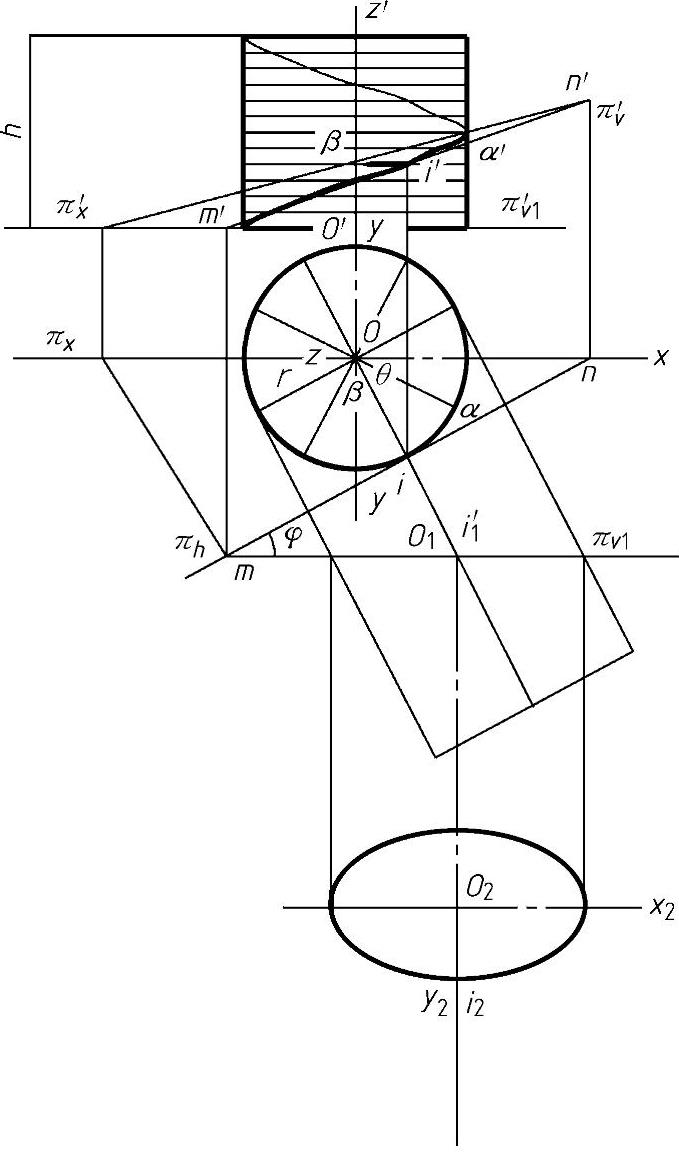
图4-70 圆柱面螺旋线上点的曲率

将这些关系代入平面曲线曲率方程可得

对i₂点有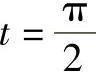，故得

也即i₂点的曲率半径

即此为圆柱螺旋线上任意点I的曲率半径。结合图4-70，以及a、b的求解过程可知，a、b与θ无关，因此对圆柱螺旋线来说，其上各点的曲率半径是相同的。