1.两共轭曲面的概念
共轭曲面是指有一定运动关系的一对相互接触的曲面,如图4-63所示,一对曲面∑1、∑2各自绕轴线O1O1、O2O2连续旋转,并始终保持相互接触,这对曲面就称为共轭曲面。两共轭曲面在运动过程中始终沿一条空间曲线相切,这条曲线称为共轭曲面的接触线,如图4-63中的曲线J。接触线具有以下性质:
1)接触线上的点均为两共轭曲面的共有点。
2)两共轭曲面在接触点处必定相切,并在接触点上对两曲面具有公共的法线或切平面。
3)为使两共轭曲面连续运动,在接触点处两曲面的相对运动速度必垂直该点处两曲面的公法线。
由图4-63可知,如果将接触线分别绕各自的轴旋转,即形成原来的两共轭曲面,因此为求出共轭曲面的形状,可先作出其接触线,然后绕给定轴回转形成。根据共轭曲面接触线的概念可知,接触线上各点对两曲面来说具有公共法线。图4-64中曲线J0为两共轭曲面∑1、∑2的接触线,可以证明,当其中一个曲面为回转曲面时(例如∑2)组成它们接触线的点,其法线必与回转曲面∑2的轴线O2O2相交。证明略。
这一概念可以作为确定共轭曲面接触线的依据。但是用图解方法确定共轭曲面接触线时,往往不能直接运用这一概念,因为无法确定∑1上哪些点的法线和所求回转曲面∑2的轴相交。为此,需要从回转曲面∑2的轴线O2O2上的各点向曲面∑1作法线来求得接触线。当两共轭曲面∑1、∑2中有一个是回转曲面时,它们的接触线是回转曲面∑2的轴线O2O2在∑1曲面上的投影。下面讨论当已知表面为某一曲面时,求与之共轭的曲面形状的作图方法及接触线和共轭曲面方程的建立。
2.共轭曲面的作图方法及接触线和共轭曲面方程的建立
在图4-65中,已知表面为圆柱面∑1,其轴线为O1O1,半径为R,与其共轭的曲面∑2的轴线为O2O2,O2O2与X轴的夹角为α,与O1O1轴间的公法线距离为L。根据这些已知条件,两共轭曲面接触线的作法如下:
1)根据已知条件作出两轴线O1O1、O2O2,为使下面的作图方便将O1O1轴置于铅垂位置,O2O2轴处于正平位置,此时正面投影面反映两轴线的夹角α。

图4-63 共轭曲面的接触线
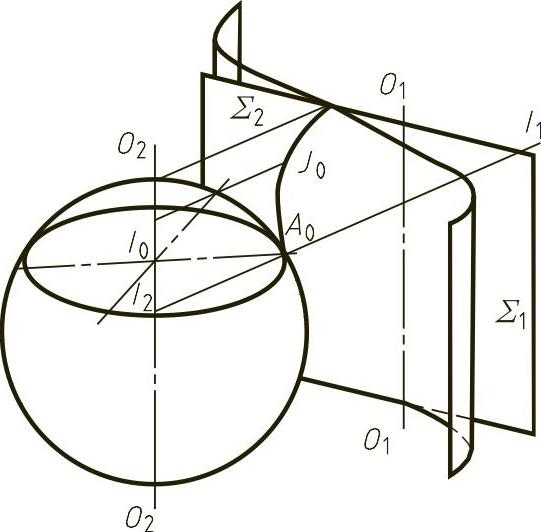
图4-64 接触线的形成
2)在O2O2轴上取一点如图中I0点。
3)连接I0点和O1O1轴线的水平投影得i0o1,该直线与圆柱水平投影相交于i,i即为接触点I的水平投影。
4)由于圆柱面上各点法线均与圆柱面轴线相垂直,故法线I0I为水平线,由此可得出I点的正面投影i′。
5)在O2O2轴线上取一系列点,按上述作图可得O2O2轴线在圆柱面上的投影。该投影代表了一条空间曲线,即圆柱面与轴线为O2O2的旋转曲面的接触线。
6)为求出轴线为O2O2的旋转曲面的投影轮廓,变换H面使H1面垂直于O2O2轴,然后将I点绕O2O2转到Ip(ip1,ip′),Ip点即为以O2O2为轴线的旋转曲面投影轮廓线上的点。
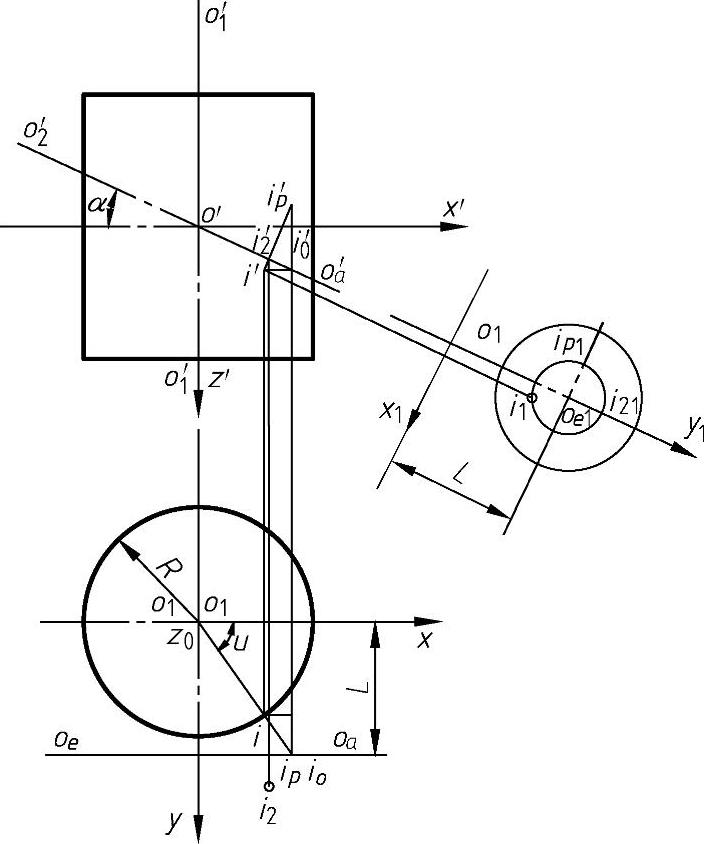
图4-65 圆柱面接触线的求作
7)在接触线上取一系列点,按步骤6)中的作图方法可得这些点旋转后的新位置,然后用曲线将它们光滑地相连即得轴线为O2O2的旋转曲面的正面投影轮廓线。
8)在正面投影中,将i′、ip′两点相连得直线i′ip′,i′ip′与O2′O2′轴线交于i2′,i2′是I点绕O2O2轴旋转到最前位置时的正面投影,由i2′不难求得i2,i2即为轴线是O2O2轴的旋转曲面水平投影轮廓线上的点。
9)按步骤8)可求得轴线为O2O2的旋转曲面的水平投影轮廓线。
根据上述作图过程,可建立接触线与共轭曲面的方程。由图4-65知O2′O2′方程为
z=(tanα)x
I0点坐标为

I点坐标为

当考虑式(4-113)中参数u的变化范围时,即可得接触线的方程

式(4-114)即为两共轭曲面的接触线方程。一次投影变换后,i1点在O1x1y1坐标系中的坐标为

I1点绕O2O2轴旋转到ip1位置后,其正面投影ip′点的坐标为

i′ip′与O2O2交点i2′的坐标由

确定得

当考虑参数u的变化范围时,可得共轭曲面的正面及水平面投影轮廓线方程分别为

在图4-66中,已知表面为锥面∑1,设其轴线为O2O2,其与X轴的夹角为α,O1O1、O2O2两轴的公垂线距离为e,O1O1上的垂足至锥顶S的距离为h。其共轭曲面接触线与投影轮廓线的作图步骤为:
1)根据已知条件作出两轴线及圆锥面的两面投影。
2)在O2O2轴上任取一点I0,过I0点作圆锥面的法线,此法线在I0点和圆锥面轴线O1O1所构成的平面内,将此平面绕O1O1轴旋转到正平位置,I0点转到IV位置,过iV′作圆锥轮廓投影线s′m′的垂线得垂足j′,再由j′求得j。然后将J点绕O1O1轴线反向旋转到圆锥素线SI上得接触点I(i,i′)。
3)按上述作图求出O2O2轴线在圆锥面上的投影即得两共轭曲面的接触线。
4)一次投影变换,将H面变换为H1面,使H1面垂直于O2O2轴线,然后将I点绕O2O2轴旋转到I1p位置,得I1p点在 投影体系中的投影I1p(i1p,ip′),其中ip′就是曲面∑2的正面投影轮廓线上的点。
投影体系中的投影I1p(i1p,ip′),其中ip′就是曲面∑2的正面投影轮廓线上的点。
5)求出I点绕O2O2轴旋转到I2位置时的水平投影i2,i2就是曲面∑2水平投影轮廓线上的点。

图4-66 圆锥面接触线的求作
根据上述作图过程,可建立接触线及曲面∑2的方程。由图4-66可知O2′O2′的方程为
z=(tanα)x (4-120)
I0点坐标为

IV点坐标为

s′j′方程为
(H-z)tanλ=x (4-123)
iV′、j′方程为

j′点的z坐标由式(4-123)和式(4-124)可得

在图4-66中,s′k′方程为

由此可得I点的坐标为

当考虑参数u的变化范围时,即可得接触线方程为
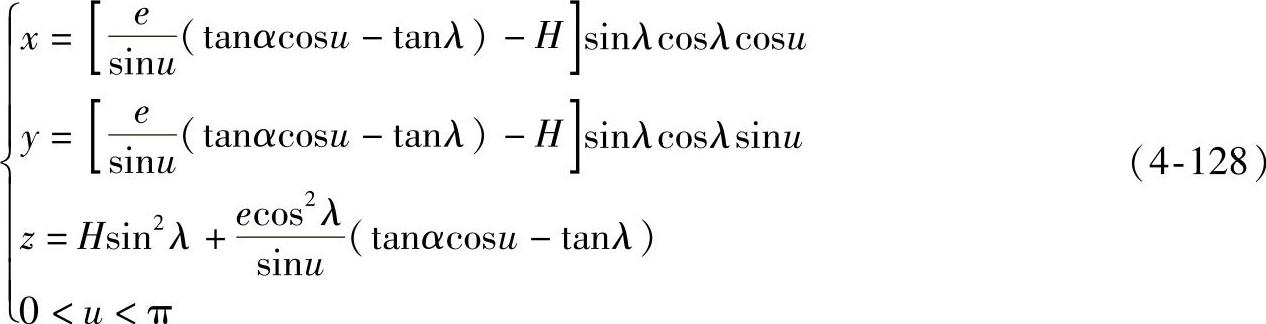
i′i′p与O2′O2′的交点i2′的x坐标可由O2O2轴线及i′ip′直线方程确定为

一次投影变换后I点的x1、y1坐标为

式(4-130)中x1、y1为I点的x、y坐标,由式(4-127)确定。
由此可得i′点的坐标为
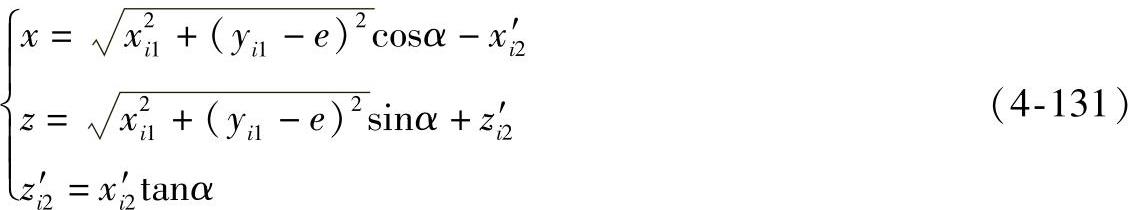
当考虑参数u的变化范围时,可得曲面∑2的正面投影轮廓线方程为
 (https://www.xing528.com)
(https://www.xing528.com)
曲面∑2的水平投影轮廓线方程由图4-66可知,应为

在图4-67中,已知表面为球面∑1,设球面球心为O,半径为R,其共轭曲面∑2的轴线为O2O2,它与X轴的夹角为α,球心O与O2O2轴的位置由a、e决定。共轭曲面的接触线与曲面∑2的投影轮廓线的作图步骤如下:
1)根据已知条件作出球心O及轴O2O2的两面投影。
2)在轴线O2O2上任取一点I0,过I0点作球面的法线,该法线即为连线OI0,过OI0作一铅垂面,将此铅垂面绕过球心O的铅垂轴线转至正平面,其上直线OIV即为正平线,o′iV′与球面正面投影轮廓线的交点j′为法线OI与球面的交点I绕铅垂轴旋转到正平面上的投影,由j′可求得j。然后将J点反向旋转到I点位置得I(i,i′),I点即为接触线上的点。
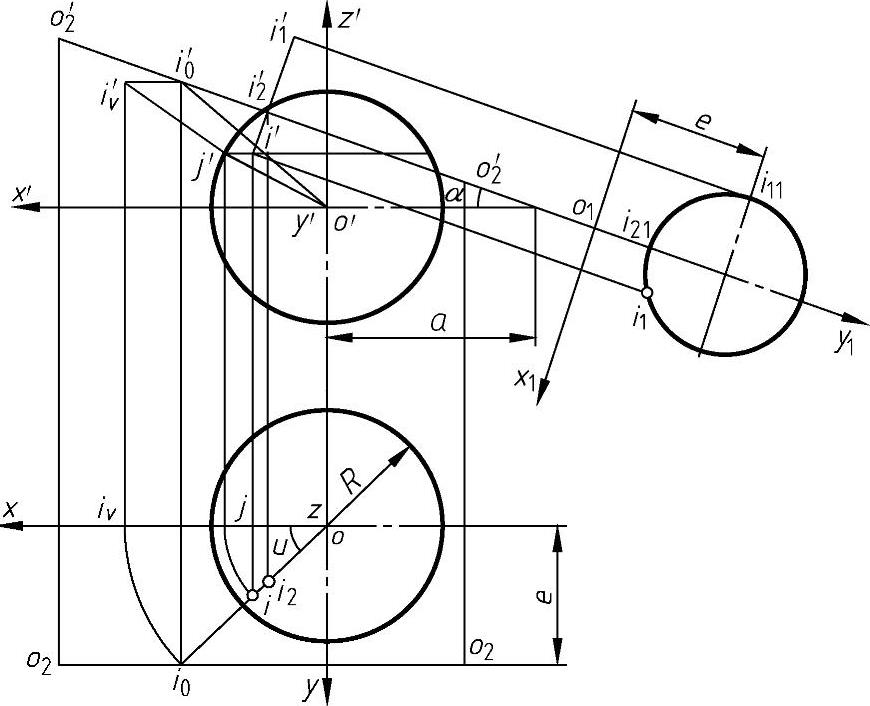
图4-67 圆球面接触线的求作
3)根据上述作图方法,可求出O2O2轴在球面上的投影,即得接触线的投影。
4)一次投影变换,将H面变换成H1面垂直于O2O2轴,然后将I点绕O2O2轴转到I2位置,ip′即为曲面∑2正面投影轮廓线上的点。
5)将I点绕O2O2轴旋转到I2位置,i2为曲面∑2的水平投影轮廓线上的点。
根据上述作图过程可建立接触线及曲面∑2投影轮廓线的方程。由图4-67可知,O2O2的方程为
z=tanα(x+a) (4-134)
I0点坐标为

IV点坐标为

故有o′iV′方程为

而球面正面投影轮廓线方程为
x2+z2=R2 (4-138)
由式(4-137)和式(4-138)可得j′点的x坐标为

由此可得I点的坐标为

当考虑参数u的变化范围时,可得接触线方程为

由图4-67可知,在H1面上i1点的x1、y1坐标为

由此可知I点绕O2O2轴旋转时,其旋转半径实长为

将点I绕O2O2轴旋转到I1位置,则i1′是轴线为O2′O2′的旋转曲面正面投影轮廓线上的点,i1′点的坐标为

由图4-67可知,i′、i1′两点连线i′i1′与O2′O2′的交点为i2′,i2′点是I点绕O2O2轴旋转到I2位置时,I2点的正面投影,其水平投影为i2,i2的坐标为

当考虑参数u的变化范围时,可得曲面∑2的正面与水平面的投影轮廓线方程分别为

在图4-68中,已知表面为圆环面∑1,设圆环面的轴线为O1O1,母线圆半径为r,母线圆圆心轨迹圆半径为R,其共轭曲面∑2的轴线为O2O2,O2O2轴与X轴的夹角为α,a、e两参数确定了O2O2与O1O1轴线的相对位置,两共轭曲面的接触线和曲面∑2的投影轮廓线的作图步骤如下:
1)根据已知条件作出圆环面及O2O2轴线的两面投影。
2)在O2O2上任取一点I0,包含I0和O1O1轴的平面与圆环面的交线是一个圆,将此平面旋转到与V投影面平行的位置,连接iV′O′V与圆环面正面投影轮廓线交于j′,由j′可得j,再将J点绕O1O1轴反转回到I点位置,则I点即为接触线上的点。

图4-68 圆环面接触线的求作
3)按上述作图,求出O2O2轴上各点在圆环面上的投影,再用曲线把它们光滑地相连,即得两共轭曲面的接触线。
4)一次投影变换,将H面变换成H1面,使H1面垂直于O2O2轴,然后将I点绕O2O2轴旋转到Ip位置,则ip′点是曲面∑2正面投影轮廓线上的点。
5)将I点绕O2O2轴旋转到I2位置,则i2点是曲面∑2水平投影轮廓线上的点。现根据两共轭曲面接触线及曲面∑2投影轮廓线的作图过程,来建立接触线与曲面投影轮廓线的方程。
由图4-68可知,O2′O2′方程为
z=(tanα)x+a (4-147)
I0点坐标为

iV′点的坐标为

iV′j′直线方程设为
z=kx+B (4-150)
式中,k、B为待定系数,由x=R,z=0, ,
, ,可得
,可得

j′点坐标为

由式(4-152)解出

由此可得I点坐标为

当考虑参数u的变化范围时,可得接触线方程为

设i′i1′方程为

将式(4-156)、式(4-147)联立可求得i2′点的坐标为

由此得i1′点在o1x1y1坐标系中的坐标为

xi为I点的x坐标,见式(4-154)。根据式(4-158)可知I点绕O2O2轴旋转的旋转半径为

所以ii′点的坐标为

当考虑参数u的变化范围时,可得曲面∑2的正面投影轮廓线方程为

故曲面∑2的水平投影轮廓线方程为

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




