主曲率半径计算曲面交线

1.平面与曲面的交线

平面与曲面相交，交线上的点属于曲面，将交点看做是主曲率半径的端点，则求交点归结为已知线段实长和投影长求坐标差的作图。

（1）平面与圆柱面的交线 图4-56所示为圆柱被平面P截交，求交线的侧面投影。因圆柱面的一个主曲率半径为R，截交线的正面投影积聚在P_V上，交线可从正面投影着手求作，现以I点为例说明作图过程。以R为直径作一半圆，在半圆内构作直角三角形，图中i′i₀′是I点曲率半径的正面投影，将其作为半圆内圆周角的一个直角边，另一直角边即为曲率半径两端点的y坐标差，由此可求得I点的侧面投影。以此作图方法求出一系列交点的侧面投影，然后用曲线将这些点光滑相连，完成交线的侧面投影。根据这一作图方法，可建立交线方程，由图4-56可得

图4-56 平面与圆柱面的交线

（2）平面与圆锥面的交线 图4-57所示为求平面P与圆锥交线的侧面投影。设圆锥面的一个主曲率半径为R₁，截交线的正面投影积聚在P_V上，交线可从正面投影着手求作，现以I点为例说明作图过程。以R₁为直径作一半圆，在半圆内构作直角三角形，图中i′i₀′是I点曲率半径的正面投影，将其作为半圆内圆周角的一个直角边，另一直角边即为曲率半径两端点的y坐标差，由此可求得I点的侧面投影。以此作图方法求出一系列交点的侧面投影，然后用曲线将这些点光滑相连，完成交线的侧面投影。根据这一作图，其交线方程由图4-57可得

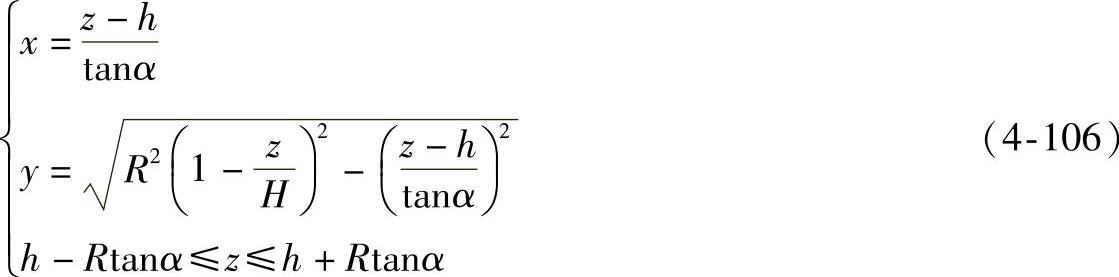
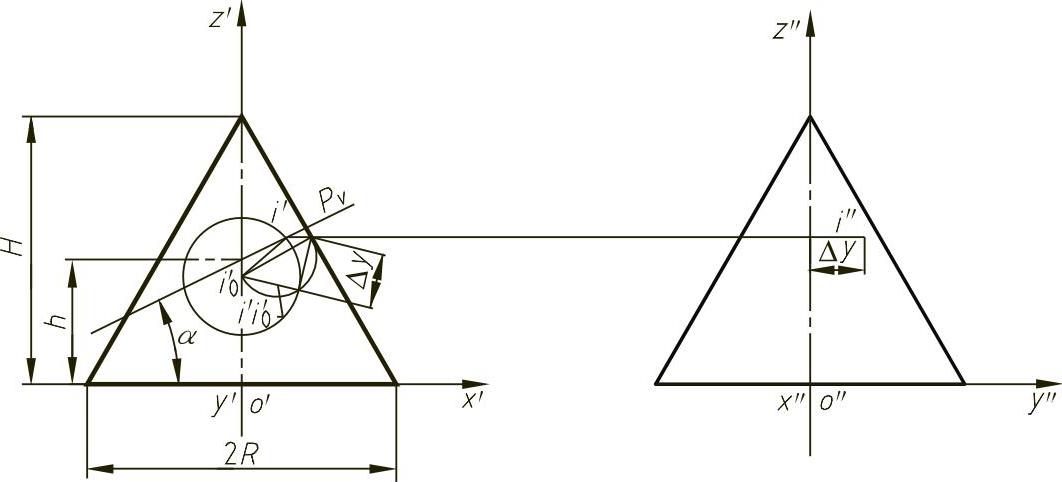
图4-57 平面与圆锥面的交线

（3）平面与球面的交线 图4-58所示为求平面P与球面交线的水平投影。设球面的一个主曲率半径为R，截交线的正面投影积聚在P_V上，交线可从正面投影着手求作，现以I点为例说明作图过程。以R为直径作一半圆，在半圆内构作直角三角形，图中o′i′是I点曲率半径的正面投影，将其作为半圆内圆周角的一个直角边，另一直角边即为曲率半径两端点的y坐标差，由此可求得I点的侧面投影。以此作图方法求出一系列交点的侧面投影，然后用曲线将这些点光滑相连，完成交线的侧面投影。根据这一作图，交线方程由图4-58可得

（4）平面与圆环面的交线 图4-59所示为求平面P与圆环面交线的侧面投影。设圆环面的一个主曲率半径为R₁，截交线的正面投影积聚在P_V上，交线可从正面投影着手求作，现以I点为例说明作图过程。以R₁为直径作一半圆，在半圆内构作直角三角形，图中i₀′i′是I点曲率半径的正面投影，将其作为半圆内圆周角的一个直角边，另一直角边即为曲率半径两端点的y坐标差，由此可求得I点的侧面投影。以此作图方法求出一系列交点的侧面投影，然后用曲线将这些点光滑相连，完成交线的侧面投影。根据这一作图，交线方程由图4-59可得

图4-58 平面与球面的交线

(www.xing528.com)

图4-59 平面与圆环面的交线

（5）平面与旋转椭球面的交线 图4-60所示为求平面P与旋转椭球面交线的水平投影。设旋转椭球面的一个主曲率半径为R₁，截交线的正面投影积聚在P_V上，交线可从正面投影着手求作，现以I点为例说明作图过程。以R₁为直径作一半圆，在半圆内构作直角三角形，图中i₀′i′₁是I点曲率半径实长，以i′₀i′作为半圆内圆周角的一个直角边，另一直角边即为曲率半径两端点的y坐标差，由此可求得I点的水平投影。以此作图方法求出一系列交点的水平投影，然后用曲线将这些点光滑相连，完成交线的水平投影。根据这一作图，交线方程由图4-60可得

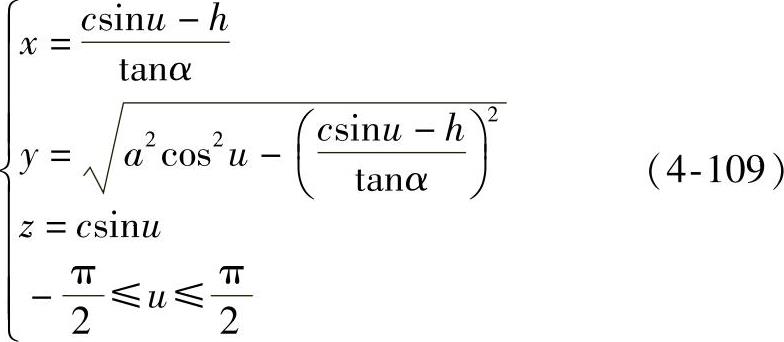
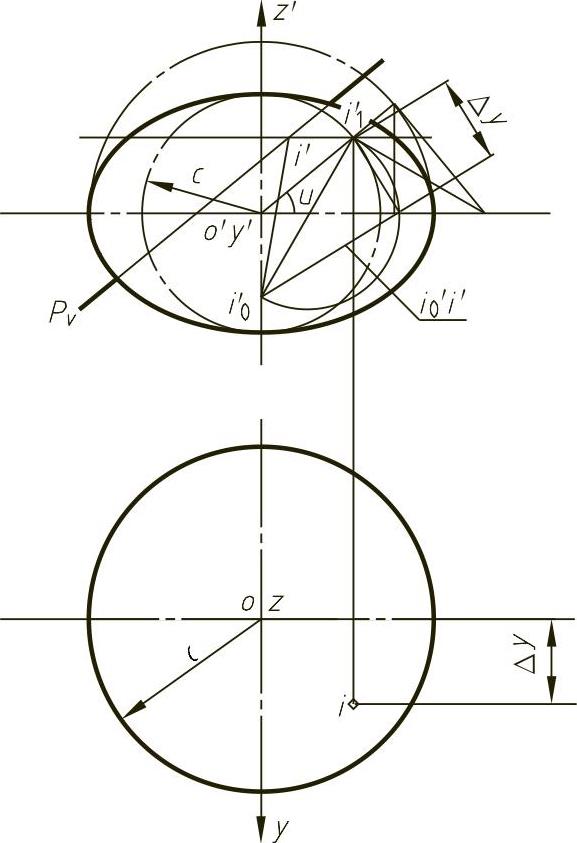
图4-60 平面与旋转椭球面的交线

2.两曲面的交线

两曲面相贯线上的点属两曲面共有，将其看做是曲面上曲率半径的端点，就可将求交线上点的作图转化为已知线段实长和坐标差求投影长的作图。

（1）圆柱与圆锥相交 图4-61所示为两轴线垂直偏交的圆柱与圆锥的投影，要求相贯线的投影。从已知投影i″着手，i′必在过i″的一条水平线上，将I点看做是圆锥面上主曲率半径I₀I₁的一个端点，已知I点的曲率半径I₀I₁=i₀′i′₁，且知I₀I两点的坐标差Δy，则不难求出I₀I₁的投影长i₀′i′₁，从而确定i′，仿此作图可求过一系列相贯线上点的投影，相贯线方程由图4-61可得

图4-61 圆柱与圆锥的交线

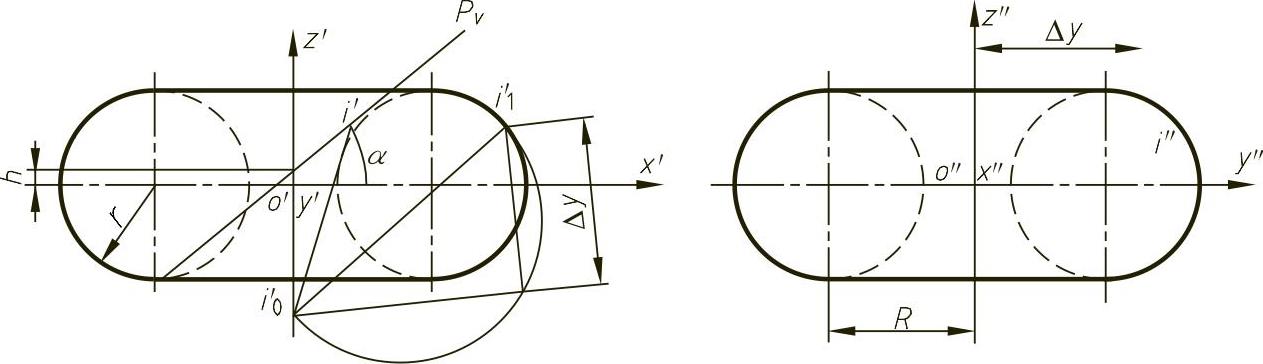
图4-62 圆柱与圆柱的交线

（2）两圆柱相交 图4-62所示为两轴线倾斜偏交的圆柱的投影，要求相贯线的投影。由已知投影i₁着手，i′必在过i₁的一条与斜圆柱轴线平行的线上，将I点看做是直立圆柱面上主曲率半径的一个端点，已知I点的主曲率半径I₀I=R，且知I₀I两点的坐标差Δy，则不难求出I₀I的正面投影长i₀′i′，从而确定i′，仿此作图可求出一系列相贯线上点的投影，交线的方程由图4-62可得