曲面上点的高斯曲率-计算机实验工程图形学.下册

在求得曲面上P点的法线后，包含法线作一平面，此平面将与曲面交于一条平面曲线，称为法截线。法截线在P点的曲率称为法曲率。显然，过曲面上P点可以做出无数条法截线，其中必有一条法截线的法曲率为最大，而另一条法截线的法曲率为最小。这两个法曲率就称为曲面在P点的主曲率k₁、k₂。曲面在P点的弯曲情况常用高斯曲率K来描述，K的表达式为

K=k₁k₂

1）K＞0，P点称为椭圆点，这时过P点的切平面与曲面仅有一个公共点，且在曲面上，通过该点所有的线都位于切平面的一侧，如图4-50所示。

2）K=0，P点称为抛物点，这时P点的切平面沿曲面的直母线相切，如图4-51所示。

3）K＜0，P点称为双曲点，这时P点的切平面与曲面相交于一系列点，如图4-52所示。

对回转曲面而言，曲面上点的两个主曲率中心的位置k₁₀、k₂₀如图4-53所示。曲面上P点与回转轴构成一平面π，平面π与回转曲面交线为C，称C为经向线，曲线C在P点的曲率中心k₁₀就是P点的一个主曲率中心，连接P、k₁₀两点得直线Pk₁₀，Pk₁₀就是P点的法线方向，延长Pk₁₀与回转轴交于k₂₀点，k₂₀即为P点的另一个主曲率中心位置。

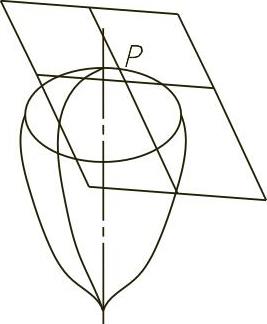
图4-50 线都位于切平面一侧

图4-51 切平面沿直母线相切于曲面

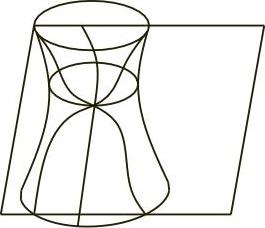
图4-52 切平面与曲面相交于一系列点

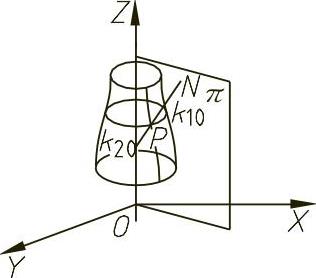
图4-53 旋转曲面的曲率中心k₁₀、k₂₀位置

1.圆锥面的主曲率半径

图4-54所示为圆锥面的两个投影，因圆锥面是直纹曲面，其轴线与锥面上点I构成的平面与圆锥面的交线是直线，故知I点的一个主曲率半径为无穷大，即

R₁=∞ （4-100）(www.xing528.com)

而另一个主曲率半径由图4-54可知

I点的高斯曲率为K=0

2.圆环面的主曲率半径和高斯曲率

图4-55所示为圆环面的两个投影，其上点I的主曲率半径求解方法如下：

1）过I点作曲面的切平面T及法线IN。

2）求IN与回转轴的交点J。再求出IJ的实长R₂，R₂为I点的一个主曲率半径。

3）圆环面的另一个主曲率半径R₁为旋转轴与I点所构成的平面与圆环面的交线在I点的曲率半径。

至此，由图4-55可得I点的主曲率半径为

I点的高斯曲率为

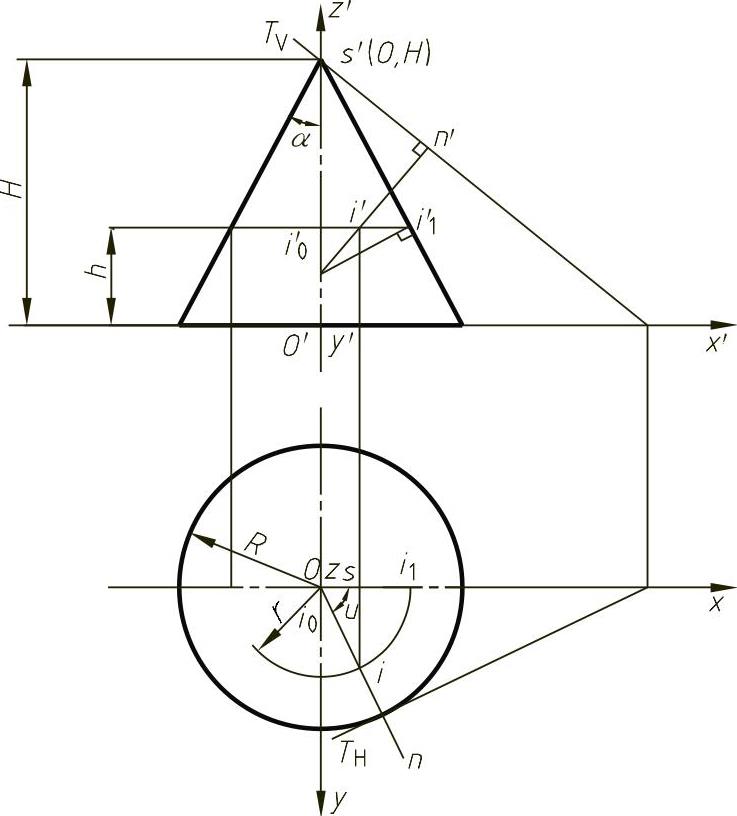
图4-54 圆锥面主曲率半径

图4-55 圆环面主曲率半径