计算机实验工程图形学下册：空间曲线曲率和挠率分析

首先研究空间曲线的曲率的概念，在不同的曲线或者同一条曲线的不同点处，曲线弯曲的程度可能不同，例如半径较大的圆弯曲程度较小，而半径较小的圆弯曲程度较大，如图4-33所示。

又如图4-34所示，当沿着曲线从左向右移动时，曲线弯曲的程度变小，为了准确地描述曲线的弯曲程度，引进曲率的概念。

图4-33 曲线的弯曲程度

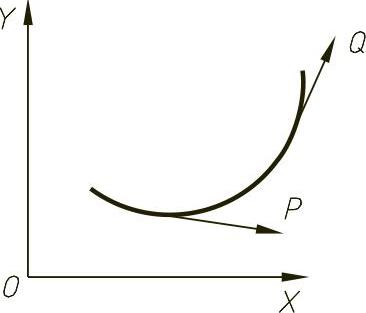
图4-34 曲线的弯曲程度变化

要从直观的基础上引出曲率的确切定义，首先注意到，曲线弯曲的程度越大，则从点到点变动时，其切向矢量方向改变得越快，所以作为曲线在已知一曲线段PQ的平均弯曲程度可取为曲线在P、Q间切向矢量关于弧长的平均旋转角。

设空间中C³类曲线（C）的方程为

r=r（S）

曲线（C）上一点P，其自然参数为S；另一邻近点P₁，自然参数为S+ΔS。在P、P₁两点各作曲线（C）的单位切向矢量α（S）和α（S+ΔS）。两个切向矢量间的夹角为Δφ，如图4-35所示，也就是把点P₁的切向矢量α（S+ΔS）平移到点P后，两个矢量α（S）和α（S+ΔS）的夹角为Δφ。可用空间曲线在点P处的切向矢量对弧长的旋转速度来定义曲线在点P的曲率。

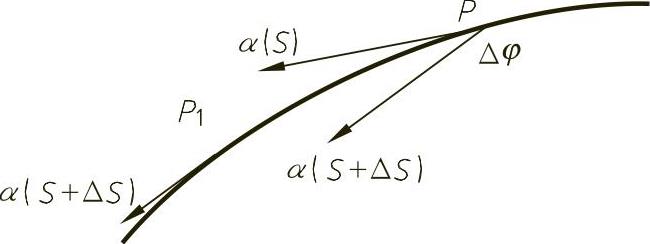
图4-35 曲线曲率的定义

定义 空间曲线（C）在点P的曲率为

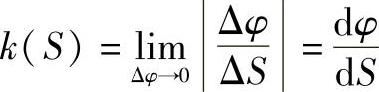
式中，ΔS为P点及邻近点P₁间的弧长；Δφ为曲线在点P和P₁的切向矢量的夹角。

空间曲线曲率半径R与其投影的曲率半径r之间的关系可由式

确定。当将空间曲线向投影面H投射时，式（4-62）中的θ为过M点的切线对H面的倾角，φ为M点处的密切平面对H面的倾角，R为空间曲线在M点的曲率半径。空间曲线在H面上投影为一条平面曲线，r是这条平面曲线在m点处的曲率半径，如图4-36所示。

证明 在M点附近取点M₁、M₂得一三角形△MM₁M₂，过此三点可作△MM₁M₂的外接圆，设其半径为R。同理，在H投影面上也可作三角形△mm₁m₂的外接圆，设其半径为r。令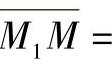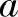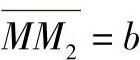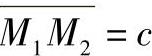，，，由平面几何知

式中，F为△MM₁M₂的面积。

同理，令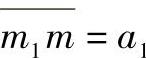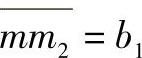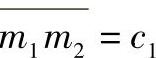，，，则有

式中，f为三角形△mm₁m₂的面积。

由式（4-63）和式（4-64）可得

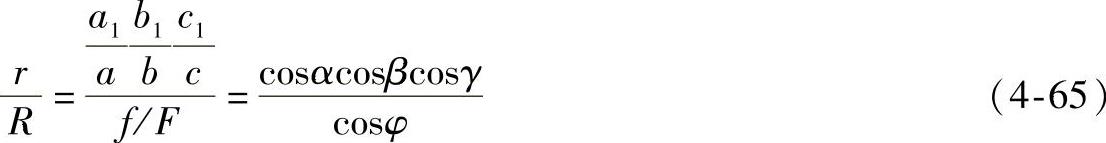
式中，α、β、γ分别为a、b、c对H面的倾角。当M₁、M₂趋近于M时，△M₁MM₂变成密切平面。a、b、c均变为切线，也即对H面的倾角均变为θ，故有

证明完毕。

根据式（4-62），当已知φ、θ、r时可用作图法求得R，如图4-37所示，其作图步骤为：

1）过O点作OA、OB、OC三条射线，使OA与OB夹角为θ，OA与OC夹角为φ。

2）在OB上量取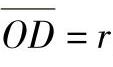，得D点，过D点作线DE⊥OB，DE与OA交于E点。

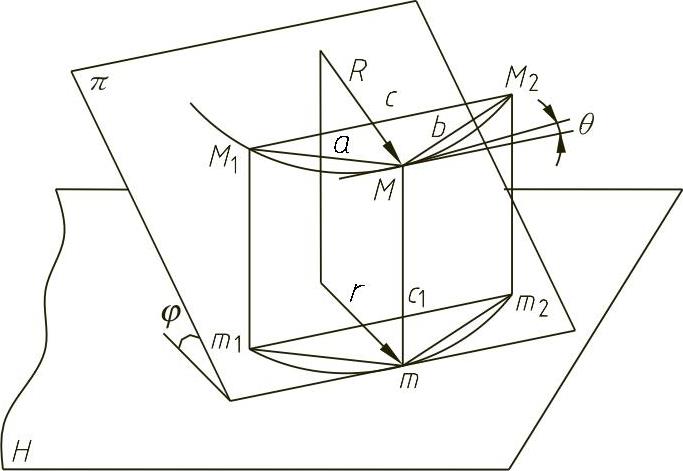
图4-36 曲线的曲率半径

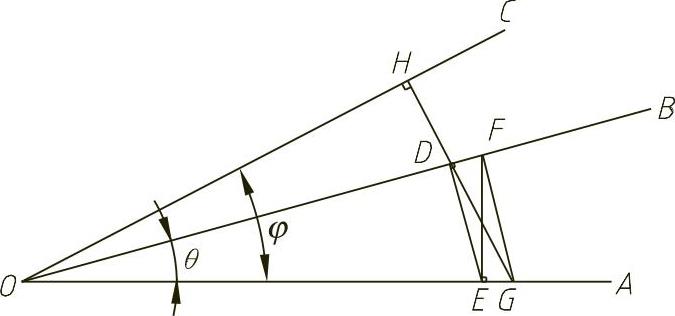
图4-37 曲率半径R的作图方法

3）过E点作线EF⊥OA，EF与OB交于F点，再过F点作线FG⊥OB，FG与OA交于G点。

4）过G点作线GH⊥OC，GH与OC交于H点。所得OH长度即为R。

例4-19 求圆柱螺旋线在M点处的曲率半径。

解 由图4-38可知，α是密切平面的最大斜度线，故有θ=φ

由

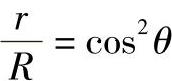
所以有

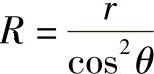
而

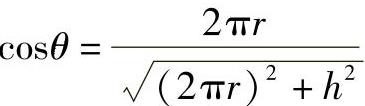
式中，h为导程。(www.xing528.com)

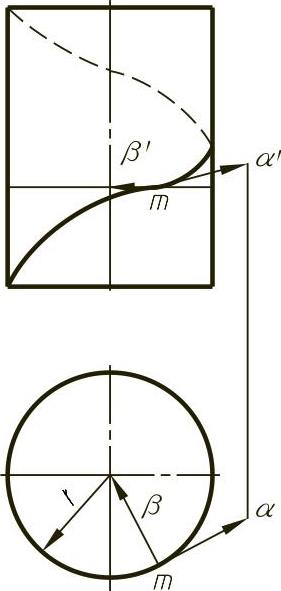
图4-38 圆柱螺旋线上点的曲率半径

将cosθ代入R关系式可得

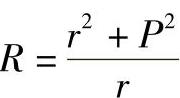
式中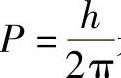，是螺旋参数。

说明圆柱螺线上点的曲率半径是常数。

例4-20 求平面P与圆柱面截交线在A、B、M点处的曲率半径，如图4-39所示。

解P面与H面成45°角，所以对A、B、M点，它们的密切平面即为P面，其与H面的夹角φ=45°，而A点处的切线与H面的夹角为θ_a=0，B点处的切线与H面的倾角θ_b=45°，M点处的切线α_M可利用直角三角形法求出。于是利用式（4-62）可求得A、B、M三点处的曲率半径分别为

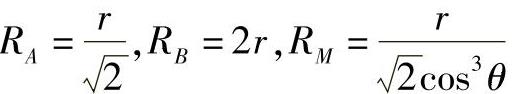
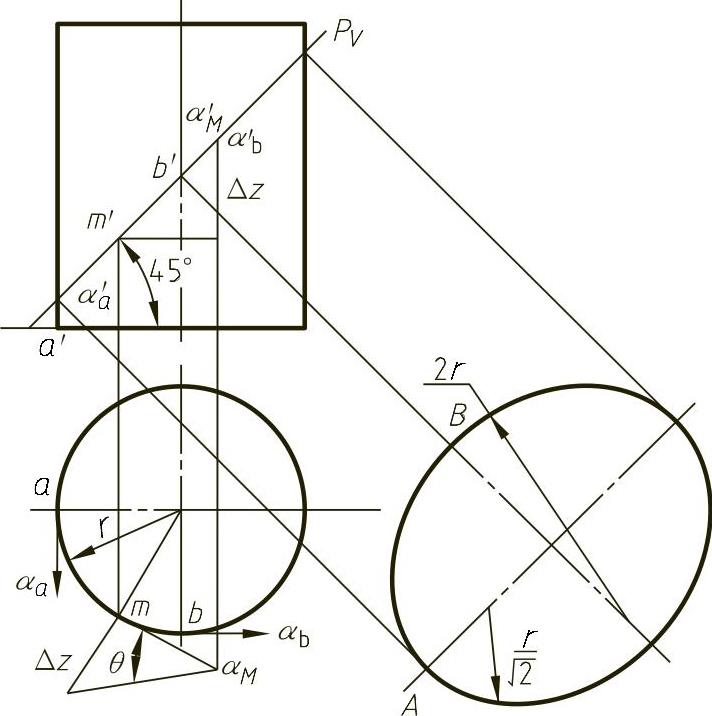
图4-39 圆柱面截交线上点的曲率半径

例4-21 由两圆柱相贯线在M点处的曲率半径R及相贯线的正面投影在m′点处的曲率半径，如图4-40所示。

解 过M点的切线是侧垂线，密切平面包含切线，所以密切平面是一个侧垂面，且密切平面又与相贯线相切，其侧面投影可在图上作出，如图4-40所示。由图可知

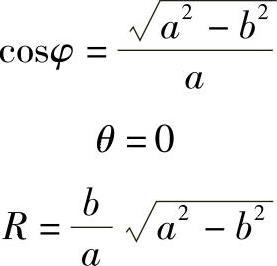
而由

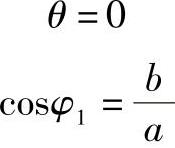
以及R可得

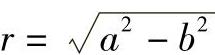
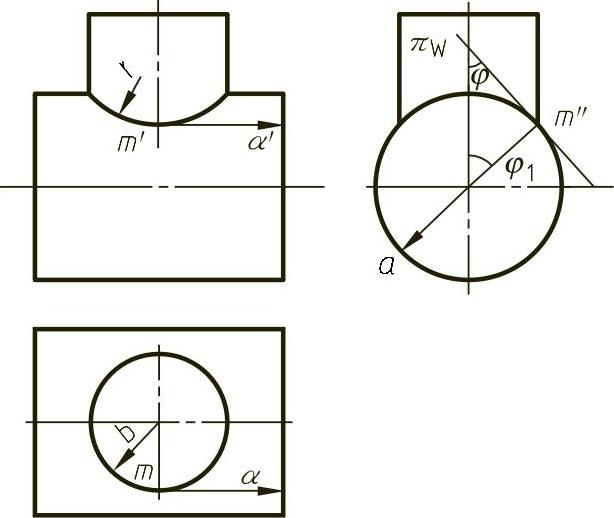
图4-40 圆柱相贯线上点的曲率半径

从另一角度看，根据空间曲线任意一点处的曲率半径等于该曲线在密切平面上的投影曲线相应点的曲率半径这一关系，可先建立曲线在任意点处的基本三棱形，然后求出曲线在密切平面上的投影即可得空间曲线在任意点处的曲率半径，如图4-41所示。

曲线在M点处的曲率半径必在β₂上，其大小可按平面曲线上点的曲率半径求解方法得出。

由上述空间曲线的曲率的定义可以看出，它的几何意义是曲线的切向矢量对于弧长的旋转速度，当曲线在一点的弯曲程度越大，切向矢量对于弧长的旋转速度就越大，因此，曲率反映了曲线的弯曲程度。

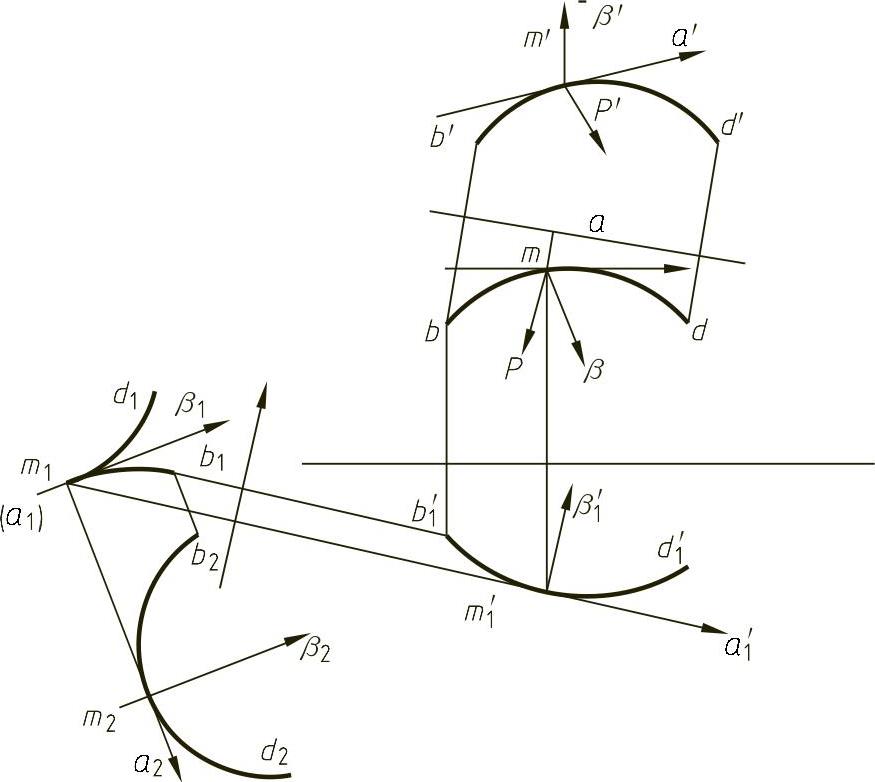
图4-41 空间曲线上点的曲率半径

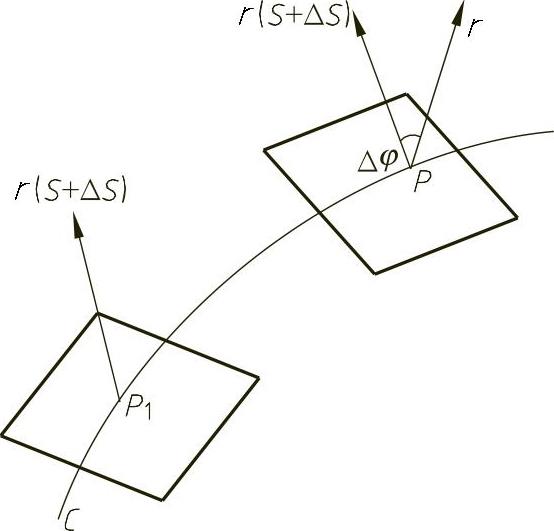
图4-42 空间曲线上点的挠率

对于空间曲线，曲线不仅弯曲还要扭转，即离开密切平面，所以研究空间曲线只有曲率的概念是不够的，还要有反映曲线扭转的程度的量——挠率。当曲线扭转时，副法向矢量或密切平面的位置随着改变，如图4-42所示。所以，可用副法向矢量或密切平面的转动速度来反映曲线的扭转程度。现设曲线（C）上一点P的自然参数为S；另一邻近点P₁的自然参数为S+ΔS在P、P₁两点各作曲线（C）的副法向矢量r（S）和r（S+ΔS），此两个副法向矢量的夹角是Δφ。

定义 曲线（C）在P点的挠率为

而挠率的倒数称为挠曲率半径ρ。根据挠率的定义，可由作图方法求解挠曲率半径ρ，如图4-43所示。其作图步骤为：

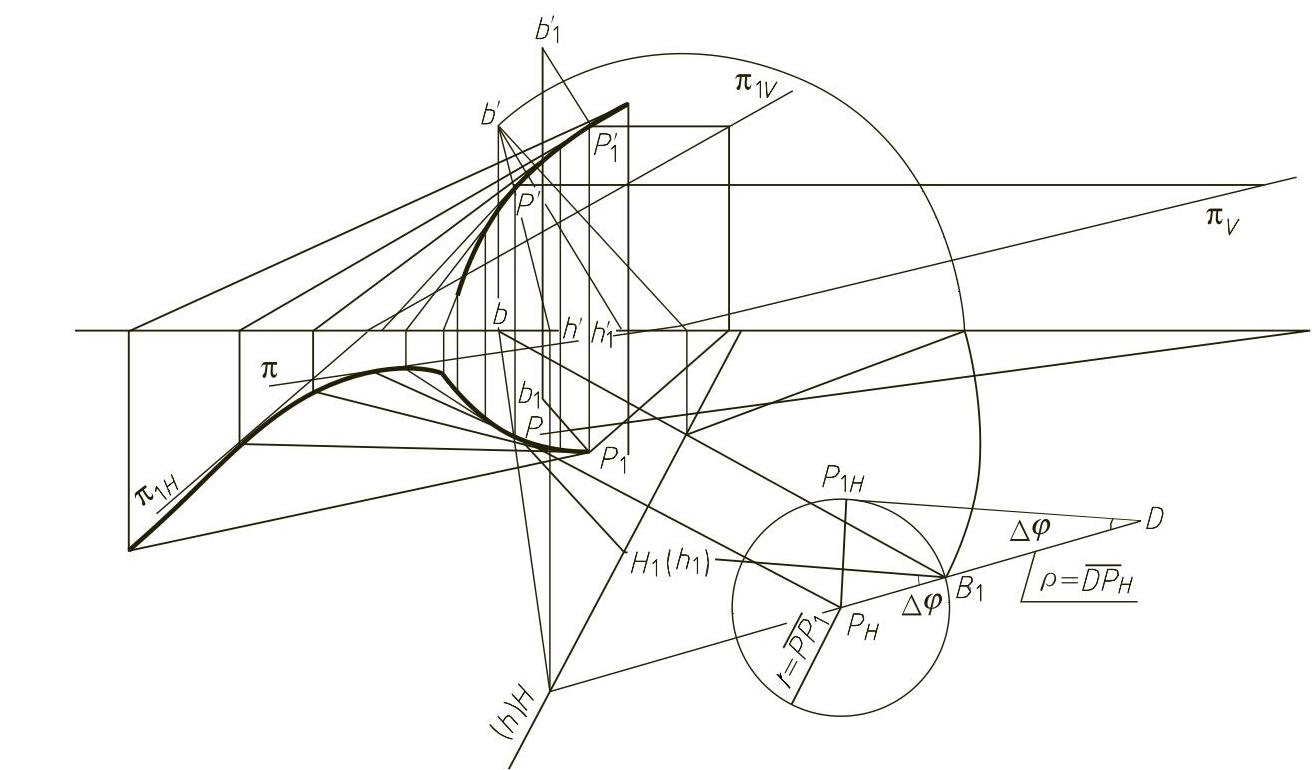
图4-43 空间曲线上点的挠率求解方法

1）求出曲线上P点及其邻近点P₁的副法线方向PB、P₁B₁。

2）过B点作P、P₁点密切平面π、π₁的垂线BH、BH₁；H、H₁分别为BH、BH₁的水平迹点。

3）以H、H₁连线为轴，将B点旋转到水平投影面上得到B₁。

4）将B₁分别与H、H₁用直线相连得B₁H、B₁H₁实长，此两线夹角即为Δφ。

5）求出P点随BH旋转后的对应位置P_H，以P_H为圆心、PP₁为半径画圆，并画此圆的切线P_1HD平行于B₁H₁，此切线交B₁H的延长线于D点。由此构成三角形ΔP_HDP_1H。在此三角形中

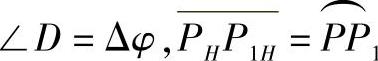
由

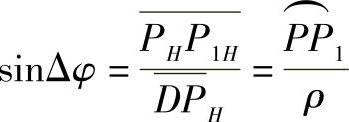
即有

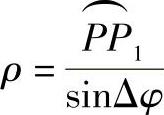
当Δφ→0时，sin=Δφ=Δφ故有

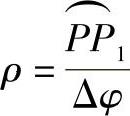
ρ即为P点的近似挠率曲率半径。