计算机实验工程图形学：空间曲线相伴三棱形

图4-27给出了空间曲线l。在曲线l上任取一点M，且过M点作切割线MA和MB，当点趋近点M时，MA将绕点M旋转，当点A与M重合时，MA就达到了极限位置α₁，割线在点M的极限位置称为曲线l在点M处的半切线；当点B与M重合时，MB位于极限位置α₂。由图4-27可见，在点M作曲线l的两条方向相反的半切线，半切线α₁和α₂构成的直线称为曲线在已知点的切线。过空间曲线上已知点的切线可以作一平面束，在平面束中有一个最贴近已知曲线的平面，称为曲线在该点的密切平面。由于包含切线的平面有无数多个，为寻找与曲线最贴近的密切平面，可以采用如下方法。

将曲线l投射到过M点且垂直于切线α的法平面Q上，如图4-28所示，则曲线l在M点的邻域部分在Q上的投影形成一条曲线C，此新曲线在M点的切向矢量为β，则α、β决定的平面就是M点的密切平面π。应用密切平面的性质，在近似计算中，如果误差要求允许曲线上某点到平面间距离满足三阶无穷小时，则可把空间曲线在这点邻域内的小曲线段转化为该点密切平面上的平面曲线来处理，从而减少问题的复杂程度，为计算带来方便。

过空间曲线l上任一点M，可以作一垂直于切线的平面，这一平面称为法平面Q。法平面与密切平面的交线称为主法线β。过空间曲线l上任一点M作一平面与主法线垂直，这一平面称为从切面P，平面Q与P的交线称为副法线γ。据上所述，过空间曲线上某一点M的三个相互垂直的平面π、Q、P形成一个直角三棱形，如图4-27所示。下面建立求解基本三棱形的作图方法。

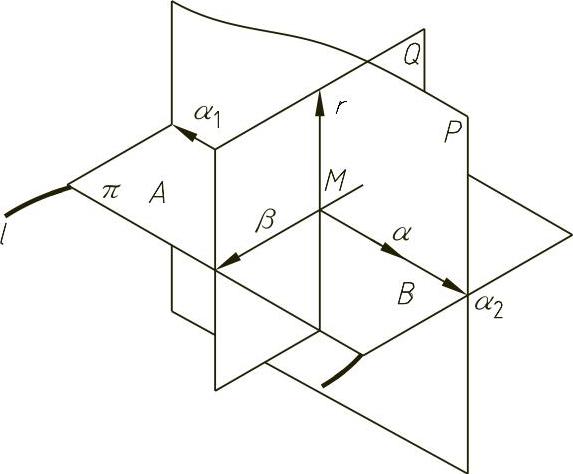
图4-27 空间曲线的相伴三棱形

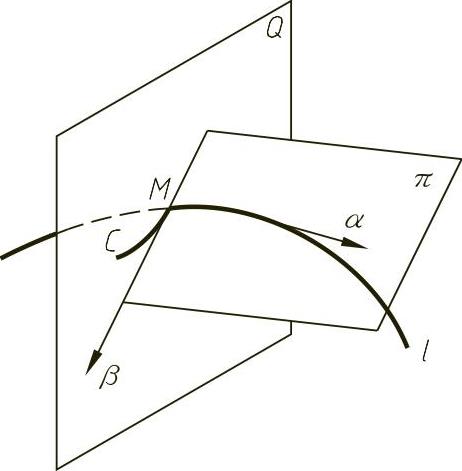
图4-28 空间曲线的密切平面

例4-16 试求圆柱螺旋线上任意一点M的基本三棱形，如图4-29所示。

1）作出M点的切线α的实长投影（一次投影变换）。

2）过M点作切线α的垂直面Q（二次投影变换）。

3）在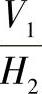体系中作出副法线γ的投影。

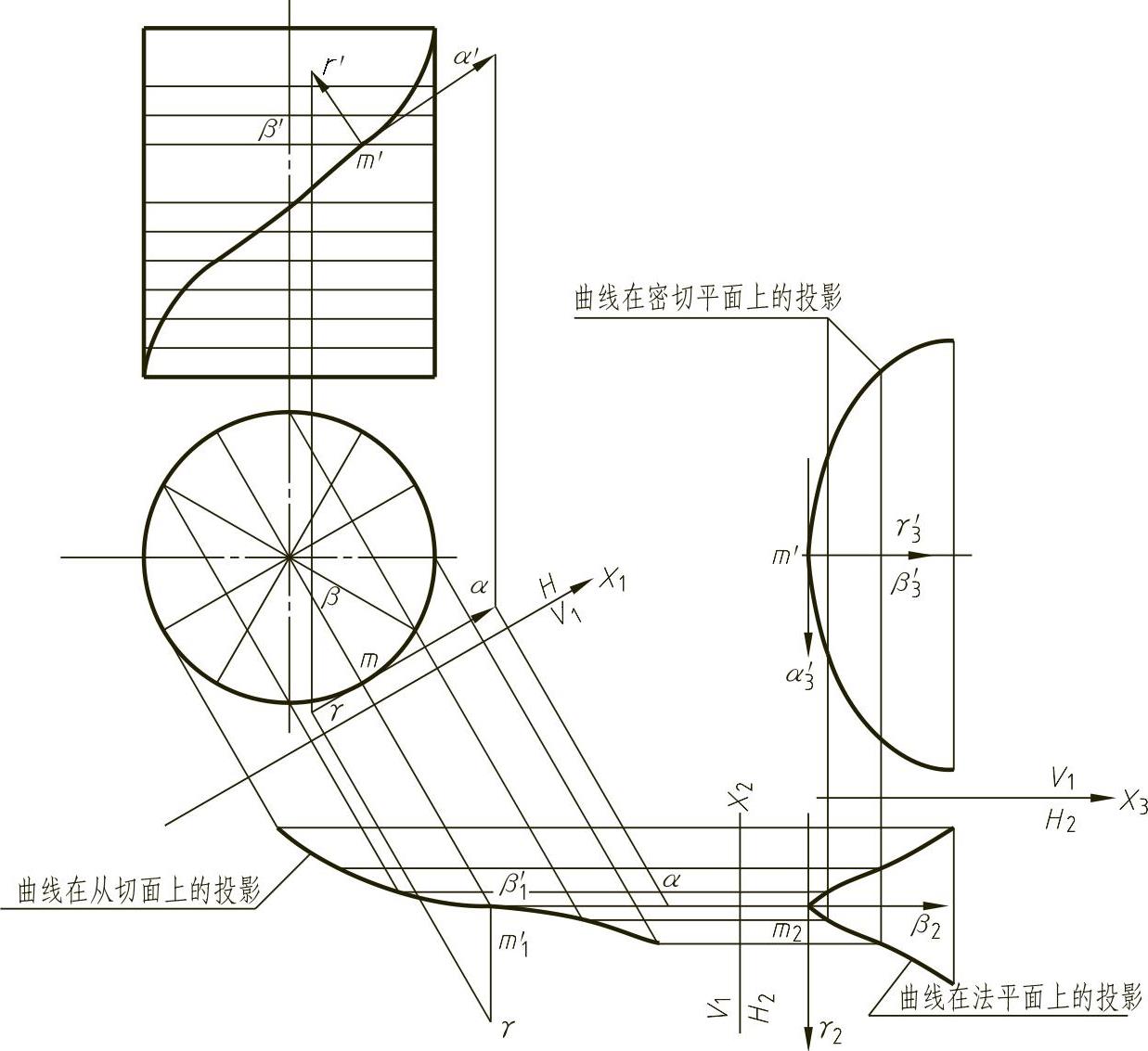
图4-29 圆柱螺旋线上任意一点M的基本三棱形

4）在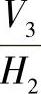体系中作出主法线β的投影。

5）投影返回求出α、β、γ在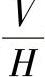体系中的投影。

根据基本三棱形的作图方法，进一步分析曲线在π、Q、P三个面上的投影，并通过曲线在此三个面上的投影来观察曲线在一点邻近的形状。

在C³类曲线r=r（S）上取一点r（S₀），为研究r（S₀）邻近的形状，在它邻近再取一点r（S₀+ΔS），如图4-30所示，利用泰勒公式有

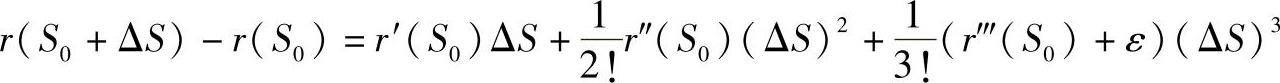
其中，。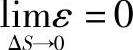

由于

r′=α

r″=Kβ

r‴=K′β+Kβ

=K′β+K（-Kα+τγ）

=-K²α+K′β+Kτγ

所以

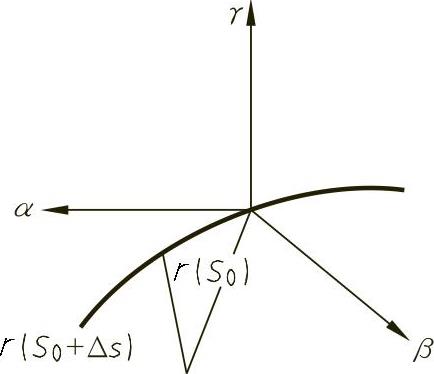
图4-30 曲线在一点处的邻近形状

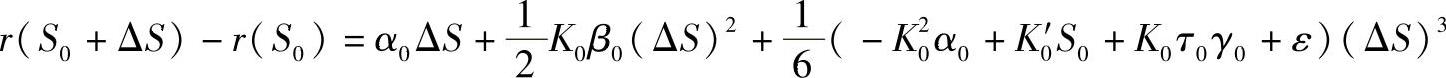
其中

ε=ε₁α₀+ε₂β₀+ε₃γ₀

而α₀、β₀、γ₀、K₀、τ₀等表示在点r（S₀）的值。

由上式可得

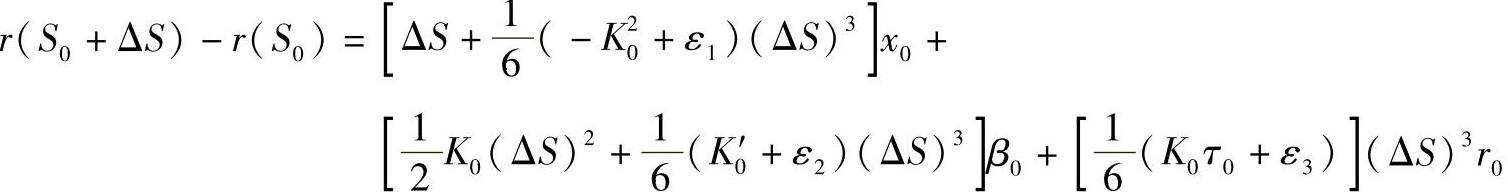
如果在α₀、β₀、γ₀的每一个分量中只取第一项则有

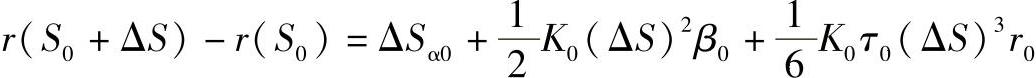
现在取[r（S₀），α₀，β₀，r₀]为新坐标系，并取r（S₀）为计算弧长的始点，则有S₀=0，ΔS=S₀，如果（ξ，ηξ）为曲线上点r（S₀）的邻近点的新坐标，则有

它可以看做在r（S₀）点邻近，曲线r=r（S）的近似方程。式中，K、τ分别为曲线在r（S₀）的曲率和挠率，由此看出曲线在某点的曲率和挠率完全决定了曲线在该点邻近的近似形状。由图4-29与式（4-50）可知，近似曲线在法平面ξ=0上的投影是一条半立方抛物线，其方程为

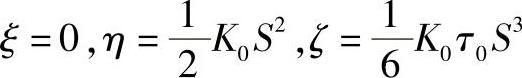
消去参数S后有

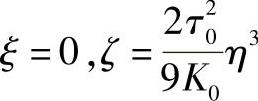
曲线在从切面_η=0上的投影是立方抛物线，其方程为

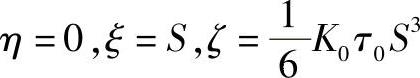
消去参数后，有

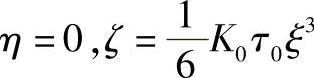
曲线在密切平面上的投影是抛物线，其方程为

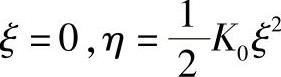
通过曲线在基本三棱形的三个平面上的投影可以看出空间曲线在一点邻近的近似形状。

曲线基本三棱形也可用另一种方法建立，如图4-31所示。其作图步骤如下：

1）在曲线l上取一系列点，过所取各点分别作曲线l的切线。

2）求出各切线的水平迹点，并将各迹点用曲线C_H光滑地相连。

3）当求曲线上M点的基本三棱形时，设过M点的切线为α，其水平迹点为x_t。显然，x_t应在曲线C_H上。

4）过α_t作曲线C_H的切线π_H，π_H即为曲线l上M点的密切平面的水平迹线。

5）由π_H及M点可求得密切平面的正面迹线π_V。

6）过M点作π平面的垂线r，r即为副法线。

7）将切线α与副法线构成的平面转化为迹线平面P，平面P即为M点的从切面。

8）过M点作平面P的垂线β，β即为主法线。(www.xing528.com)

9）过M点作平面Q与切线α垂直，平面Q即为M点的法平面。

至此，M点的基本三棱形便已作出，根据上述作图过程可以得出切线、副法线、主法线的方程及密切平面、从切面、法平面的方程。

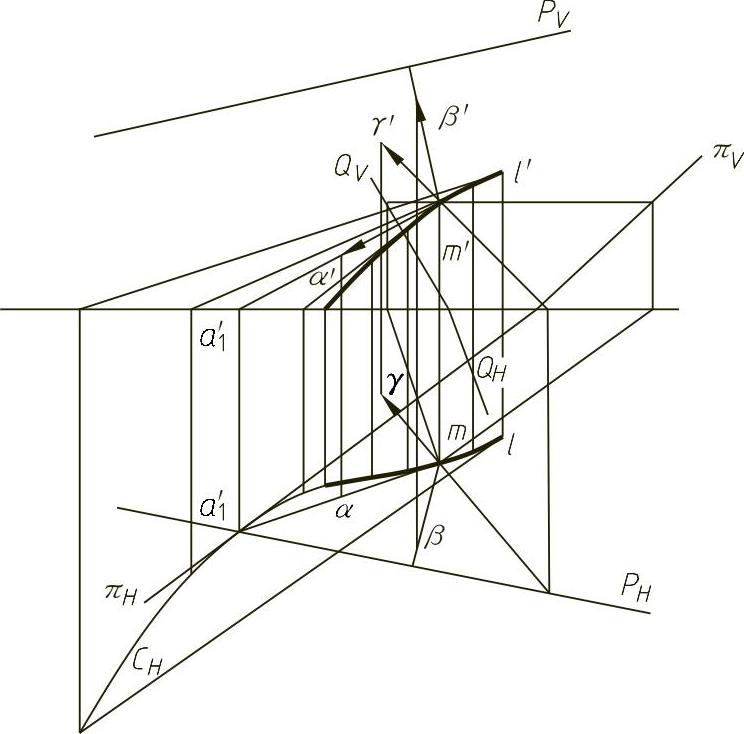
图4-31 曲线基本三棱形

设曲线l上M点的坐标为（x，y，z），而（X，Y，Z）为过曲线l上M点的切线α上某一动点的坐标，则切线α的方程为

根据作图步骤2），令式（4-51）中z=0，得水平迹点x_t的坐标为

因点M是曲线l上流动的点，所以式（4-52）实际上就是作图步骤2）中的曲线C_H的方程。因此过x_t作曲线C_H的切线π_H的方程为

式（4-53）中x^∗、y^∗为π_H上一动点的坐标，而

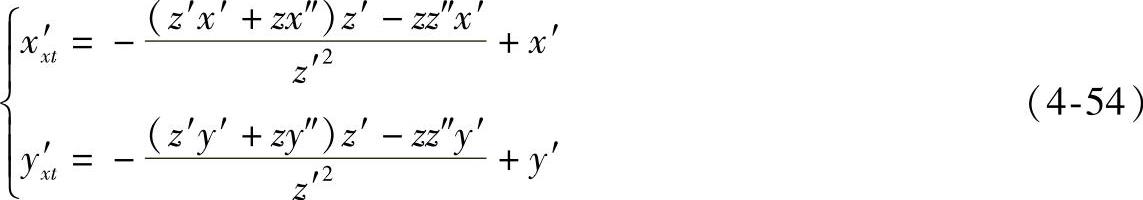
将式（4-52）、式（4-54）代入式（4-53）并加以整理可得π_H的方程为

（x^∗-x）（y′z″-z′y″）-（y^∗-y）（x′z″-z′x″）-z（x′y″-y′x″）=0 （4-55）

同理可得密切平面的正面迹线π_V的方程为

（x^∗-x）（y′z″-z′y″）+y（x′z″-z′x″）-（z^∗-z）（x′y″-y′x″）=0 （4-56）

式（4-52）、式（4-56）可合写为

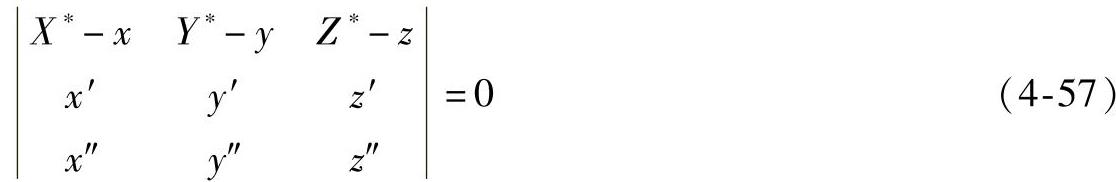
式（4-57）即为密切平面的又一表达形式。

由于副法线与密切平面垂直，故其方程为

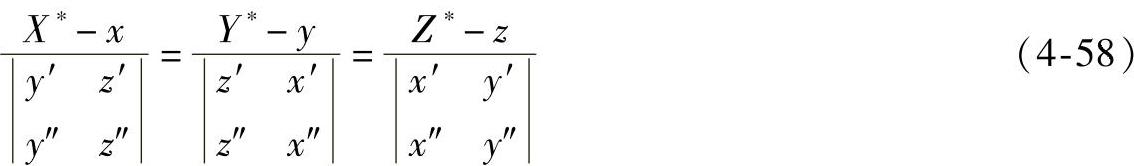
由于法平面与切线垂直，故由式（4-51）可得法平面方程为

x′（X-x）+y′（Y-y）+z′（Z-z）=0 （4-59）法平面与密切平面的交线为主法线，由式（4-57）、式（4-59）可得主法线的方程为

由于从切面与主法线垂直，故其方程为

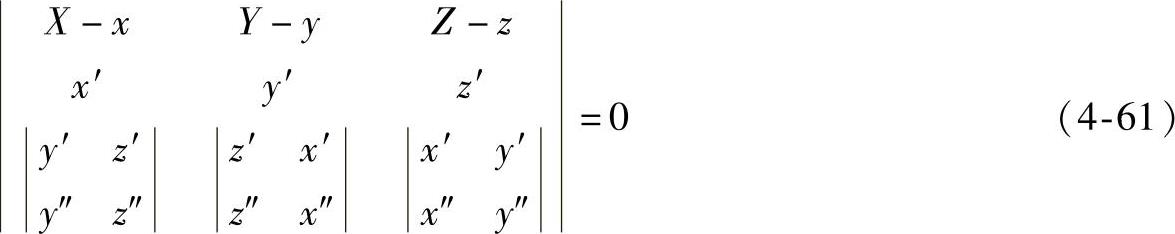
例4-17 求圆柱螺旋线x=acosθ，y=asinθ，z=bθ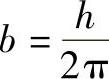，的切线、法平面、副法线、主法线和从切面方程。

解 如图4-29所示，切线方程为

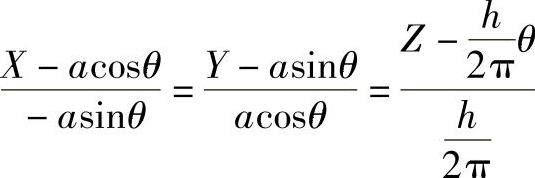
法平面方程为

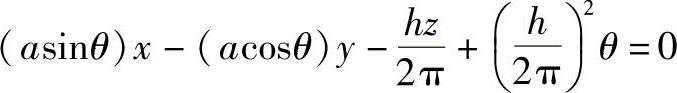
主法线方程为

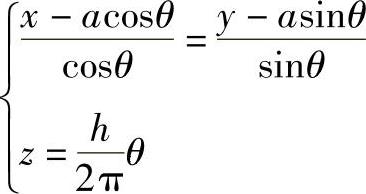
从切面方程为

xcosθ+ysinθ-a=0

例4-18 求维维安尼曲线在B点处的切线、法平面、副法线、密切平面、主法线、从切面方程，如图4-32所示。

解 由图4-32可知，维维安尼曲线为圆柱面与球面的交线，其方程为

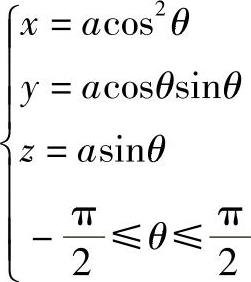
故有

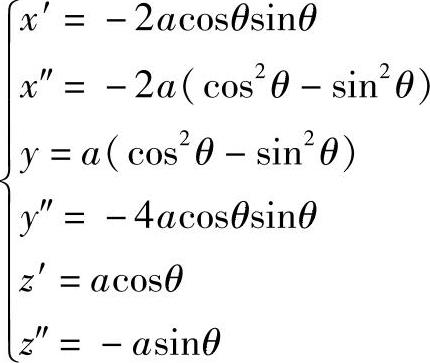
由B点处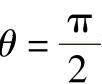得

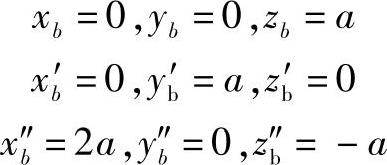
根据这些条件可得B点处的密切平面方程为

x-2z-2a=0

法平面方程为

y=0

从切面方程为

z-2x-a=0

切线方程为

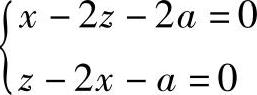
主法线方程为

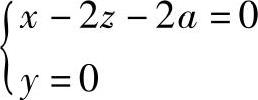
副法线方程为

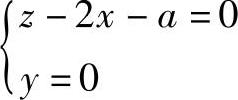
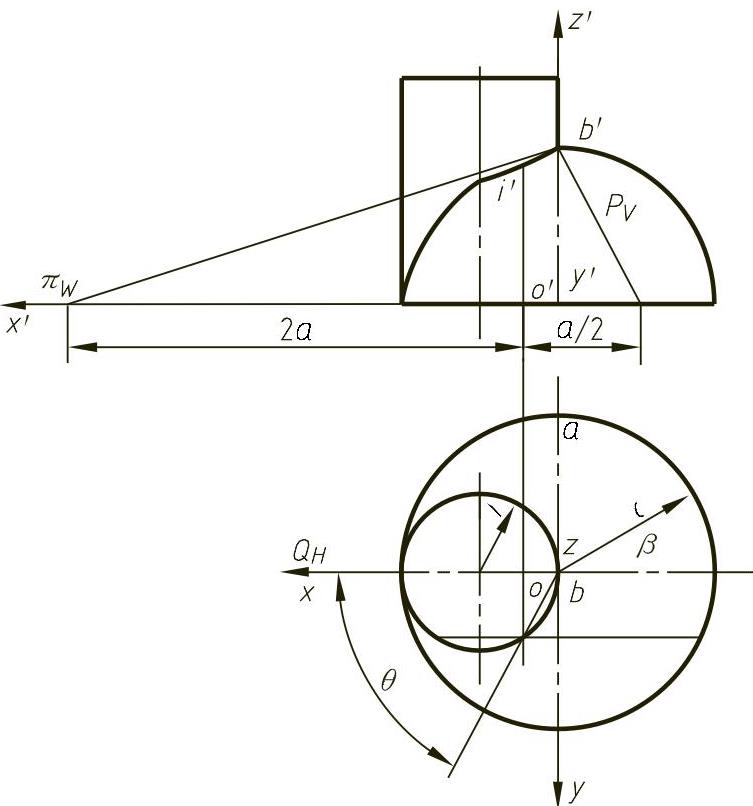
图4-32 维维安尼曲线上点的几何性质