计算机实验工程图形学下册：空间曲线表达式及微分不变量

空间曲线可以用矢量方程、弧长、参数方程或两曲面相交的交线方程来表达。如式（4-43）～式（4-46）所示。

r=r（t）=x（t）i+y（t）j+z（t）k （4-43）

r=r（S）=x（S）i+y（S）j+z（S）k （4-44）

x=x（t），y=y（t），z=z（t） （4-45）

例4-14 圆柱螺旋线的矢量表示，如图4-24所示。

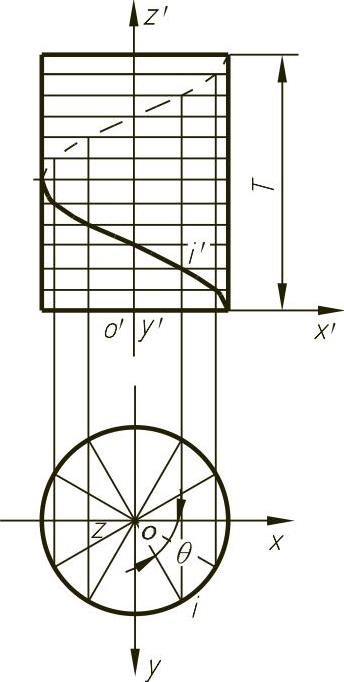
图4-24 圆柱螺旋线

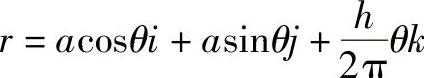
式中 h——螺距；

a——圆柱半径。

参数表达式为

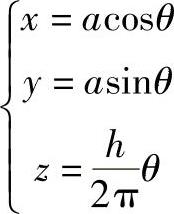
例4-15 维维安尼曲线可以用球面与圆柱面交线的形式表示，如图4-25所示。

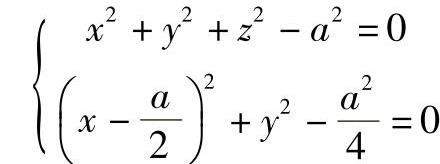
也可以用参数形式表达，由图4-25可知

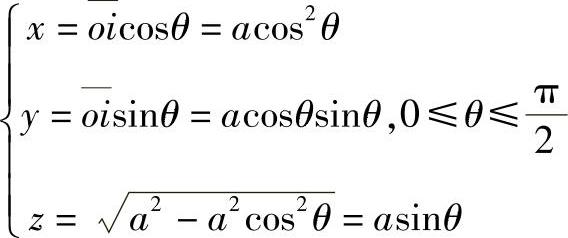
一般来说，用参数方程表达空间曲线最为普遍。当用正投影的方法表达曲线时，如图4-24和图4-25所示，曲线在投影时所保持下来的性质有：

1）曲线的切线的投影为其投影的切线。

2）点在曲线上，点的投影一定在曲线的同面投影上。(www.xing528.com)

下面讨论空间曲线的微分不变量。设空间曲线矢量方程为

r=r（t）

则r（t）的导矢量在坐标变换下是不变的。所谓坐标变换就是坐标平移、旋转或两者结合。

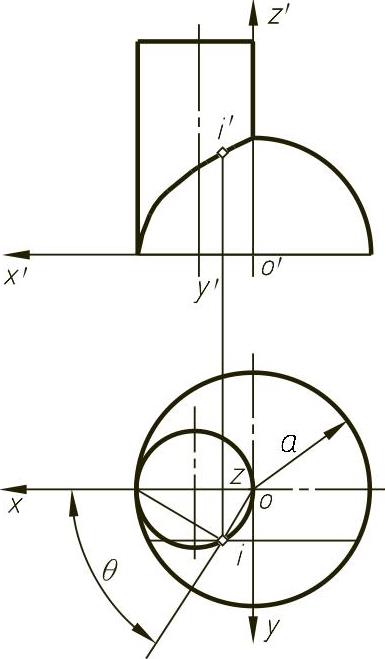
图4-25 维维安尼曲线

由图4-26知，在坐标从O变换到O^∗时，所得两个径向矢量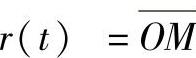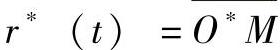，，而三角形OO^∗M，按矢量和的定义，有

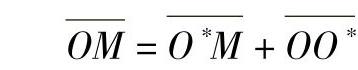
即

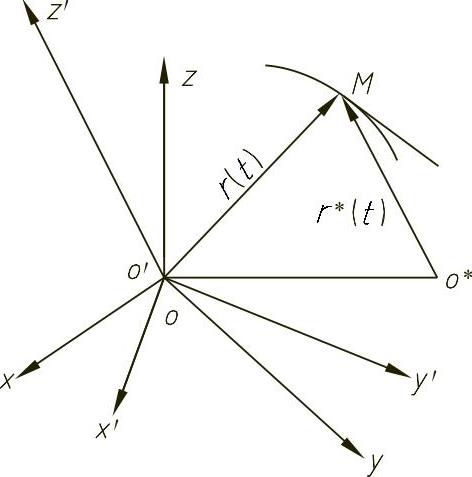
图4-26 曲线的微分不变量

这就是径向矢量在平移变换时的变换式。式（4-47）说明在平移变换下同一点M在不同坐标系中的径向矢量只差一个常矢量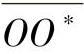，所以，它的导矢量为

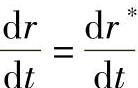
因此，在平移变换下导矢量不变。在旋转变换下，径向矢量的各阶导矢量是不变量。设径向矢量r（t）的坐标为x（t）、y（t）、z（t）；旋转后的坐标为x（t）、y（t）、z（t）；由解析几何知，两者之间有如下关系

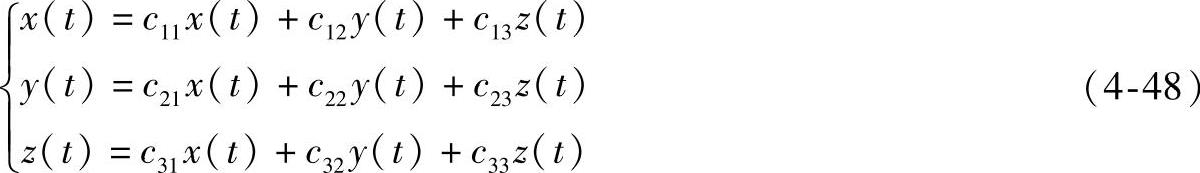
式中，c_ij（i，j=1，2，3）是坐标变换式的系数。此时因坐标原点没变，只是坐标轴的方向改变了，因此只引起它的坐标改变，而径向矢量本身并不变。

由于r（t）的各阶导矢量r（n）（t）也随着径向矢量r（t）所经过的旋转变换而变换，所以在两个坐标系中同一n阶导矢量的坐标之间也满足上述的旋转变换公式，即

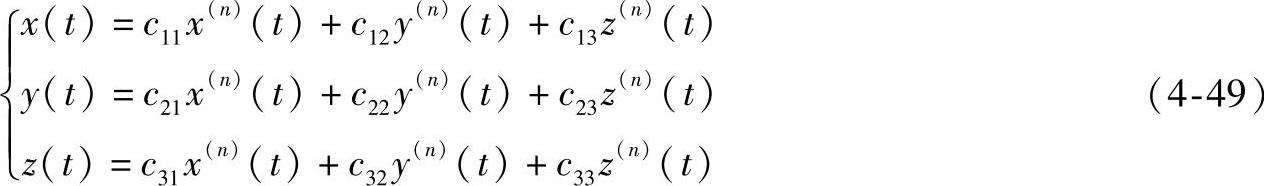
如果这些导矢量r（n）（t）都看成是附着于曲线的对应点上，则它的长度和它与曲线的相对位置经旋转变换都是不变的。