计算机图形学实验：平面曲线曲率、曲率半径和曲率中心

1.基本概念

曲线上无限接近的两个半切线之间的夹角α，对两点间弧长S之比可以表征曲线的弯曲程度。α越大，则曲线的曲率也越大，以k代表曲率，则有

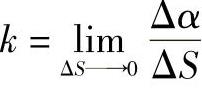
通过曲线上的点A以及与它无限接近的两个点A₁和A₂可唯一地确定一个圆C，圆C称为A点的密切圆。密切圆的半径就是曲率半径，圆心就是曲率中心。

2.计算公式

平面曲线的计算公式见表4-1。

表4-1 平面曲线的计算公式

注：表中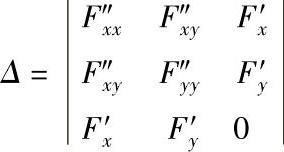

3.求二次曲线上任意点的曲率中心

（1）椭圆上点的曲率中心

1）作图。

① 过椭圆上M点作椭圆的切线T₁T₂（仿射对应方法作图），如图4-17所示。

② 过M点作MN₂⊥T₁T₂，则曲率中心必在MN₂上。

③ 过T₂作T₂B∥MN₂，与过M点所作的X轴平行线交于D点。

④ 连接D、O两点并延长与MN₂交于C点，C点即为曲率中心。

2）寻求上述作图过程的几何关系。

① 由△OBD∽△ON₁C得

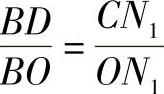
② 由△ODT₂∽△ON₂C得

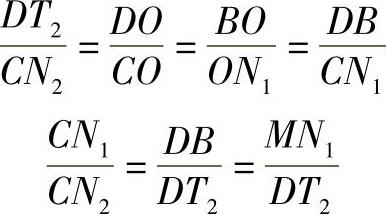
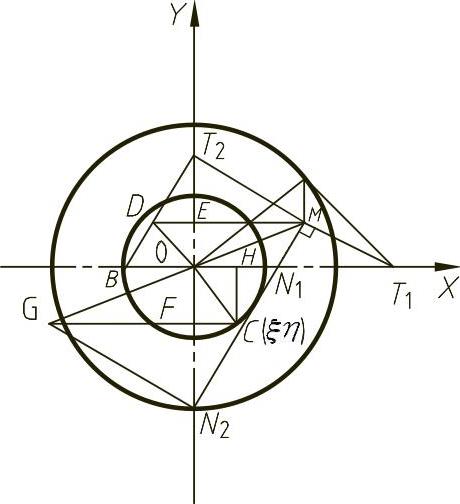
图4-17 椭圆上点的曲率中心

③ 由△T₂DM∽△MN₁T₁得

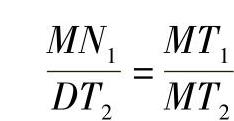
由以上关系可得

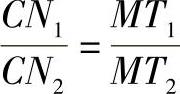
3）用解析的方法求C点的坐标及T₁、T₂、N₁、N₂点的坐标。设椭圆的参数方程为

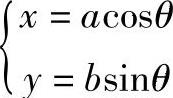
则有

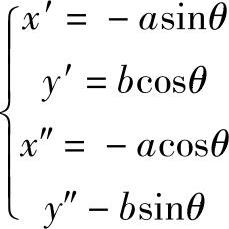
得C点坐标

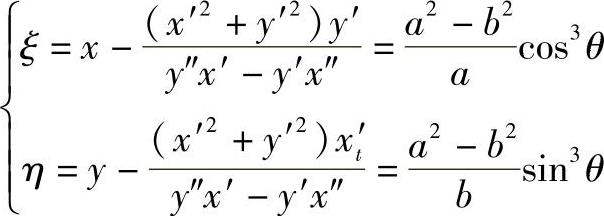
由椭圆切线方程

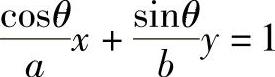
可得T₁、T₂点的坐标

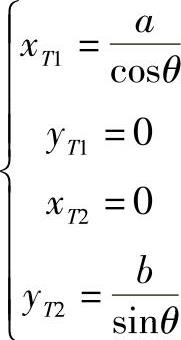
由椭圆法线方程

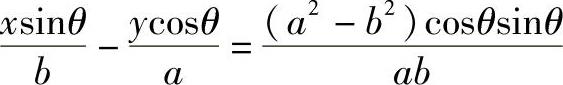
可得N₁、N₂点的坐标

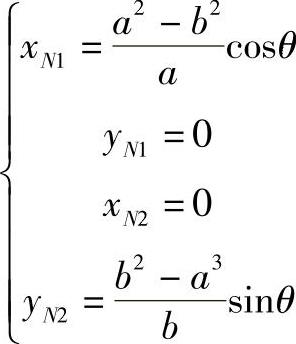
4）证明作图正确。由图4-17知△CFN₂～△N₁HC，并利用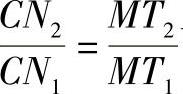可得

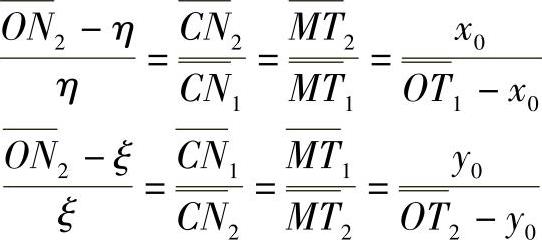
由上述两式得

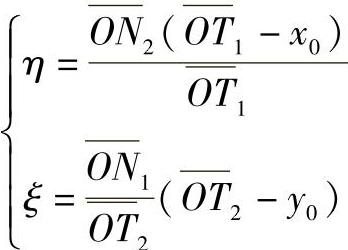
将N₁、N₂、T₁、T₂的坐标代入并注意到

x₀=acosθ，y₀=bsinθ

可得

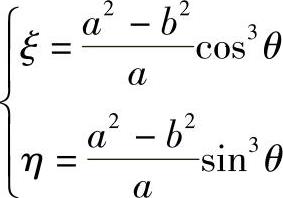
由此证明作图方法正确。

（2）抛物线上点的曲率中心 如图4-18所示，已知抛物线方程为

y²=2px

对上式求导得

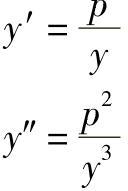
曲率中心坐标为

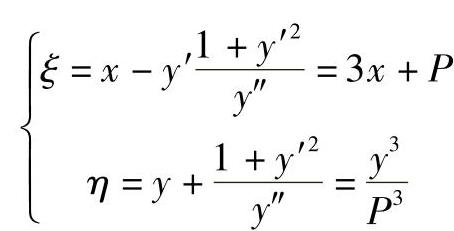
说明曲率中心C的x坐标为3x+P，而点M（x₁，y₁）处的法线与X轴的交点E的坐标由法线方程

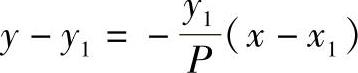
令其y=0，即可得E（x₁+p，0）。由此得出曲率中心C的作图步骤为

1）作点M（x₁，y₁）处的法线（先作切线），如图4-18所示。

2）求出法线与X轴的交点E。

3）从交点E在X轴上向右截取长度2x₁得F点。

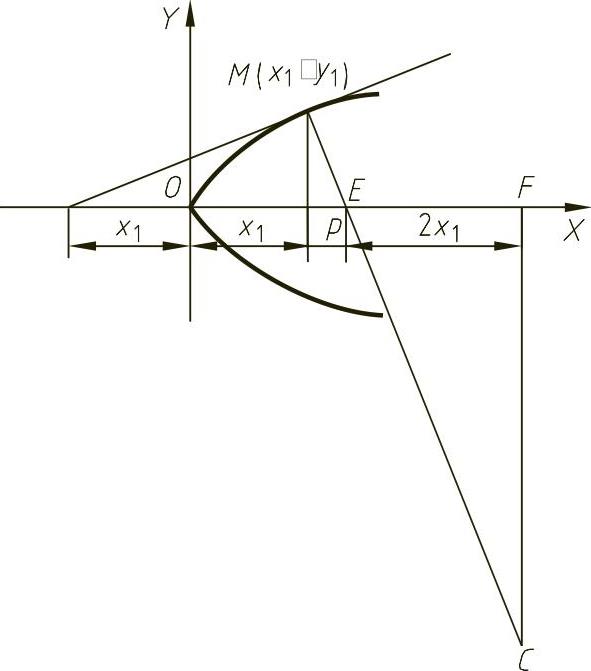
图4-18 抛物线上点的曲率中心

4）从F点作X轴的垂线与法线相交于C点，C点即为M点的曲率中心。

（3）双曲线上点的曲率中心 已知双曲线方程为

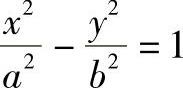
对上式求导得

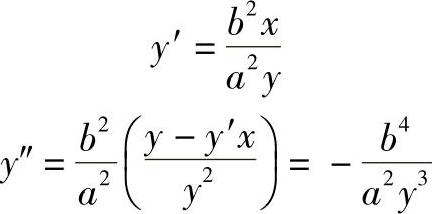
得曲率半径

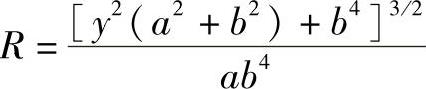
曲率中心坐标为

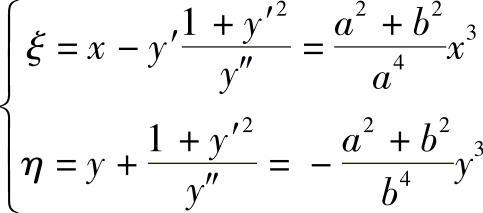
曲率中心C的作图步骤如图4-19所示。(www.xing528.com)

1）将M点与焦点F₁、F₂相连得∠F₁MF₂，作出∠F₁MF₂的角平分线MN，MN为过M点的切线。

2）MN交X轴于N点，过N点作NP//MC。

3）过M点作MS⊥X轴与NP相交于点S。

4）连O、S并延长与MC交于点C，点C即为曲率中心。

证明作图正确。双曲线的切线方程为

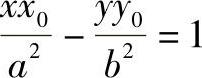
法线方程为

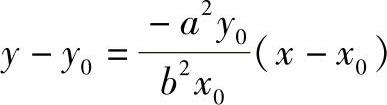
N点坐标。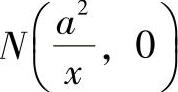

NP直线方程为

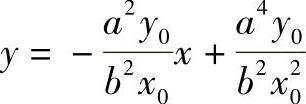
MS直线方程为

x=x0

S点坐标S。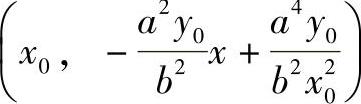

SO直线方程为

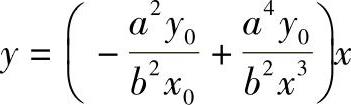
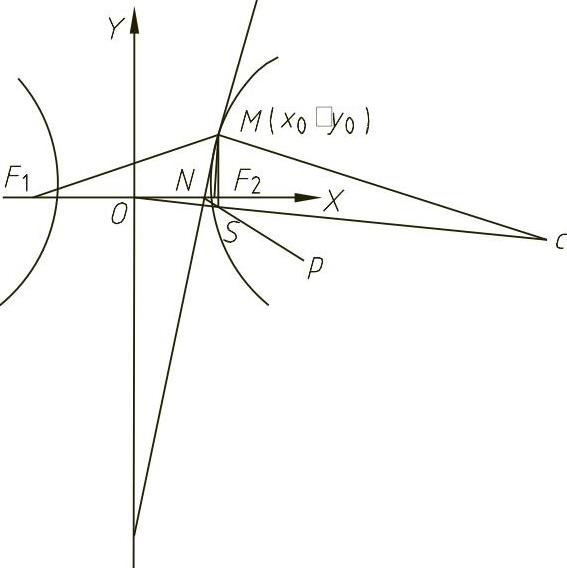
图4-19 双曲线上点的曲率中心

SO与MC的交点C的坐标由方程

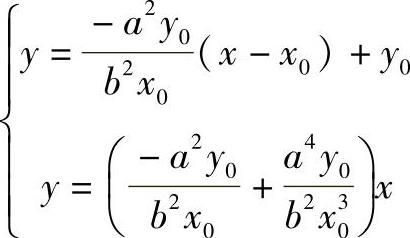
可得

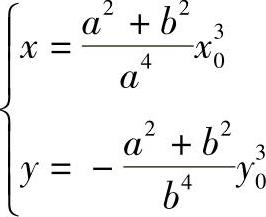
由此证明作图方法正确。

4.求平面曲线与曲率中心的一般方法

本节着重讨论平面曲线两个问题的一般求解方法：

①已知平面曲线上各点所对应的曲率中心求该曲线；②已知平面曲线，求曲线上各点的曲率中心。下面分别进行讨论。

（1）已知平面曲线上各点的曲率中心，求该曲线 当已知一条平面曲线上各点所对应的曲率中心时，若把这些中心点光滑地连成曲线，则此曲线为平面曲线的渐缩线C^∗，设渐缩线C^∗的方程为

y=f（x）

根据渐缩线C^∗求C曲线的步骤为：

1）根据方程画出C^∗，如图4-20所示。

2）在渐缩线C^∗上取一系列点Q_i（i=0，1，2，…）。

3）以Q₁为圆心、弧长为半径画圆，与过Q₁点所作渐缩线C^∗的切线Q₁P₁交于P₁点。

4）以Q₂为圆心、弧长为半径画圆，与过Q₂点所作的渐缩线C^∗的切线Q₂P₂交于P₂。

5）仿照上述作图可依次求得P₃，P₄，…。

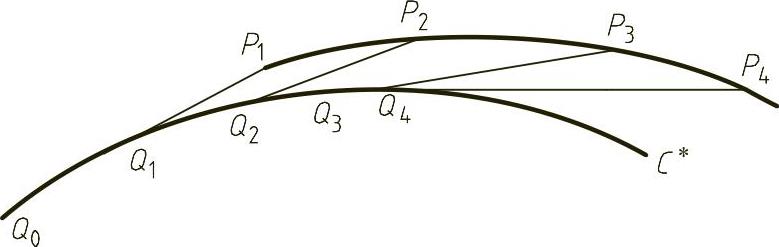
图4-20 渐缩线C∗

6）将P₁，P₂，…诸点用曲线光滑地相连，得曲线C。

由上述作图方法可知，过渐缩线C^∗上某点Q_i（x_i，y_i）的切线方程为

y-f（x_i）=f′（x_i）（x-x_i） （4-28）

而弧长为

因此，以Q_i点为圆心，以R=S为半径的圆方程为

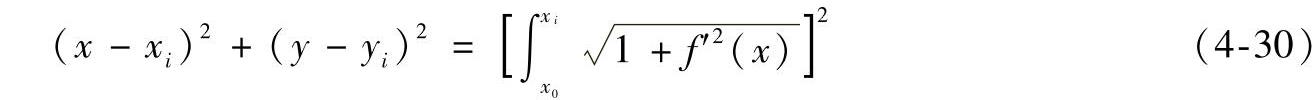
由此可知，C曲线上P_i点的坐标应满足方程

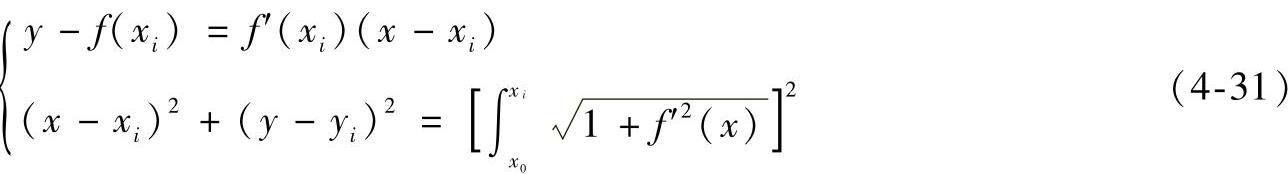
显然，当以渐缩线C^∗上点的x坐标为参数，即式（4-31）中x_i的下标i=0，1，2，…变化时，由式（4-31）可求得C曲线上的各对应点。因此，式（4-31）即为C曲线的参数方程。

（2）已知平面曲线，求曲线各点的曲率中心 该问题刚好与上述的问题相反。假设曲线l上点M_i的曲率中心为已知，则M_i点的曲率圆与曲线l在M_i点处必有公共的切线和法线。据此性质，M_i点的曲率中心求解步骤为：

1）作出曲线l上各点的切线t_i，在每条切线上取相等的长度c，得一系列端点M_i^∗（i=1，2，3，…），如图4-21所示。

2）将M_i^∗（i=1，2，3，…）诸点光滑地连成曲线l^∗，则l^∗曲线是曲线l的切向等距曲线。

3）过M_i点作曲线l在该点的法线n_i。

4）过M_i∗点作曲线l^∗在该点的切线t_i^∗。

5）过点M_i^∗点作曲线l^∗在该点的法线n_i^∗。

6）两法线n_i、n_i^∗相交于Q_i即为曲线l在m_i点的曲率中心。将各曲率中心点Q_i用曲线Q光滑地相连，曲线Q即为曲线l的渐缩线。

根据上述作图步骤，曲线Q上点Q_i的坐标求解如下，设已知曲线l的方程为

y=f（x） （4-32）

则过曲线l上M_i（x_i，y_i）点的切线方程为

y-f（x_i）=f′（x_i）（x-x_i） （4-33）

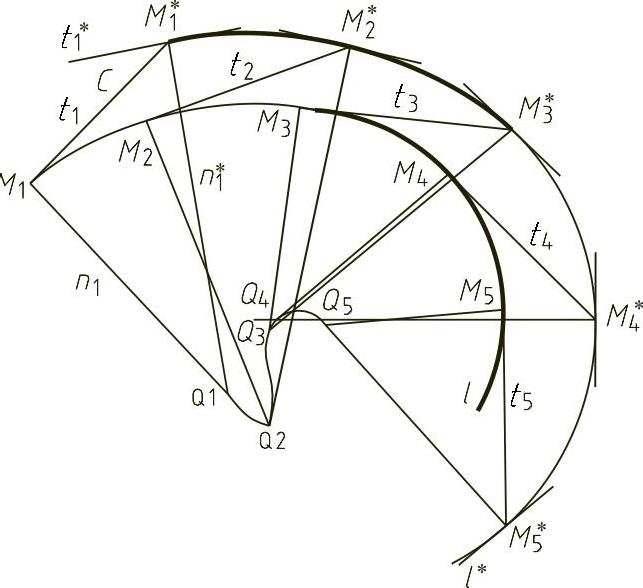
图4-21 曲线上各点的曲率中心

以M_i（x_i，y_i）点为圆心，以单位长度c为半径画圆，此圆与曲线l在点M_i的切线交于点M_i^∗，M_i^∗点就是图4-21中曲线l^∗上的点。由此可得曲线l的方程为

由式（4-34）解出x、y就是M_i^∗点的坐标。显然，x、y是x_i、y_i的函数，即有

因此，过M_i^∗点作曲线l^∗的切线t_i^∗的方程为

过M_i^∗点作曲线l^∗的法线n_i^∗的方程为

又由式（4-33）可知，过M_i点作曲线l的法线n_i的方程为

联立式（4-37）、式（4-38）得

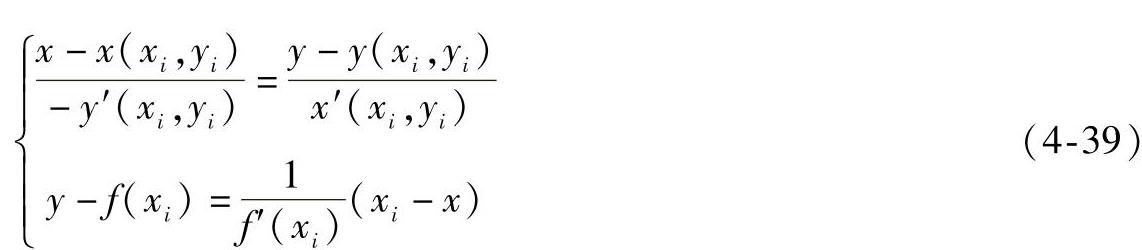
由式（4-39）解出x、y即为曲线l在M_i点的曲率中心Q_i的坐标。