【摘要】:关于平面曲线族的包络主要以两个实例说明包络线的求解方法,以及特征点的坐标和作用。例4-12 已知圆族的方程为(x-a)2+y2-=0解 求作包络线方程 由Fa′=-2(x-a)+2a=0得包络线方程为消去a得图4-16 平面曲线族的包络a)直线族的包络 b)圆族的包络即由此可知,包络线为一椭圆。
关于平面曲线族的包络主要以两个实例说明包络线的求解方法,以及特征点的坐标和作用。
例4-11 已知直线族的方程为
xcosα+ysinα+a=0
式中,α为变量;a为常量。
解 (1)求作包络线方程 由Fα′(x,y,α)=-xsinα+ycosα
得包络线方程为
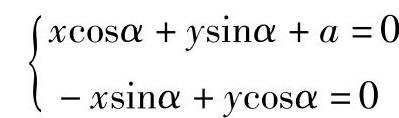
消去参数α得
x2+y2=a2
由此可知包络线为圆。
(2)求特征点——包络线与直线族中每条直线的切点 由包络线的参数方程可得特征点的坐标值
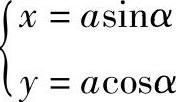
(3)图解法求特征点 由解析可知,包络线为一圆心为O、半径为a的圆,因为包络线与直线族中的每条直线均有一个切点(特征点),所以只要过圆心O作OM垂直于直线,交点M就是特征点,如图4-16a所示。
例4-12 已知圆族的方程为
(x-a)2+y2-(r2-a2)=0
解 (1)求作包络线方程 由Fa′(x,y,a)=-2(x-a)+2a=0
得包络线方程为(https://www.xing528.com)
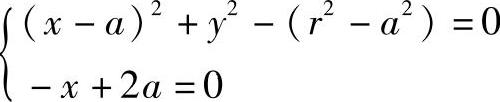
消去a得
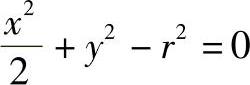
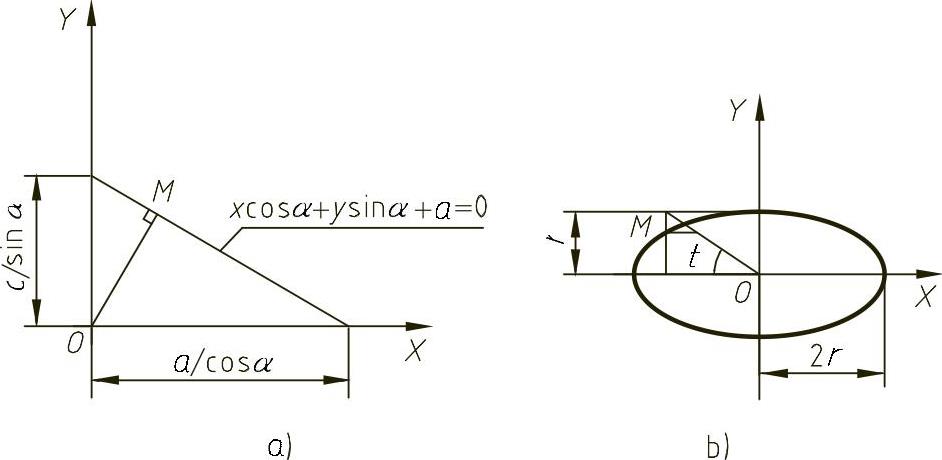
图4-16 平面曲线族的包络
a)直线族的包络 b)圆族的包络
即
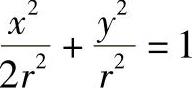
由此可知,包络线为一椭圆。
(2)求特征点 由包络线方程
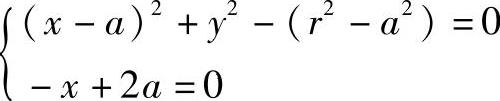
可得特征点坐标
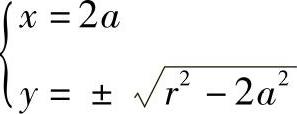
(3)作图 由特征点坐标即可求得特征点M,如当a=0,则x=0,y=±r就得到两个特征点,依次改变a就能定出相应的特征点的位置,如图4-16b所示。图中
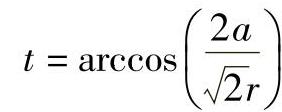
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




