【摘要】：贝塞尔曲面与贝塞尔曲线类似，由一个特征网格控制曲面的形状特征。根据图中特征网格的16个顶点，可导出特征矩阵图3-57 双三次贝塞尔曲面这样，双三次贝塞尔曲面的数学表达式可写为下面仍以孔斯曲面已知条件为例设计贝塞尔曲面。绘制贝塞尔曲面的程序LP3-43.lsp可通过扫描二维码观看，图3-58所示为程序运行后所画的贝赛尔曲面。LP3-43.lsp程序图3-58 贝塞尔曲面
贝塞尔曲面是贝塞尔曲线在空间的拓展。贝塞尔曲面与贝塞尔曲线类似，由一个特征网格控制曲面的形状特征。贝塞尔曲面的数学表达式为
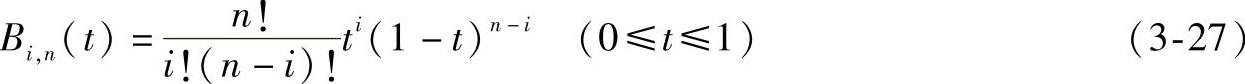
贝塞尔曲面采用伯恩斯坦基函数Bi，n（t），可用两个m次和n次的一元函数的积构成m×n次函数。贝塞尔曲面函数的矢量表达式为
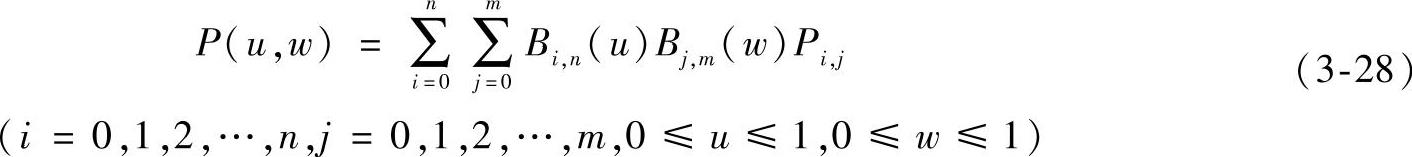
Pi，j是（m+1）（n+1）个点组成的空间点阵，依次连接点Pi，j中相邻两点组成的空间网格，称为特征网格。当m=n=1时，称为双一次贝塞尔曲面，表达式为
P（u，w）=（1-u）（1-w）P（0，0）+u（1-w）P（1，0）+（1-u）wP（0，1）+uwP（1，1） （3-29）
它表示双一次贝塞尔曲面是双曲抛物面上的一片曲面。
当m=n=2时，称为双二次贝塞尔曲面，表达式为
当m=n=3时，称为双三次贝塞尔曲面，它是通过空间已定义的4×4个网格点来控制的，如图3-57所示。根据图中特征网格的16个顶点，可导出特征矩阵
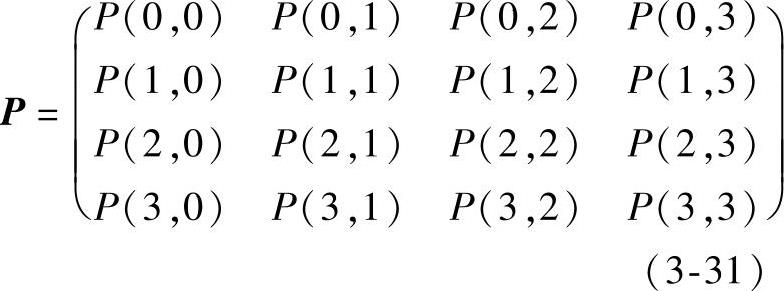(https://www.xing528.com)
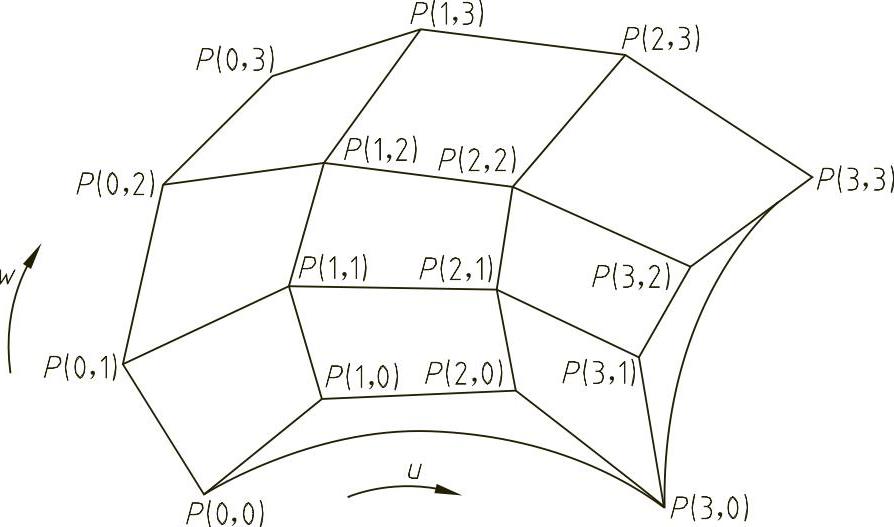
图3-57 双三次贝塞尔曲面
这样，双三次贝塞尔曲面的数学表达式可写为
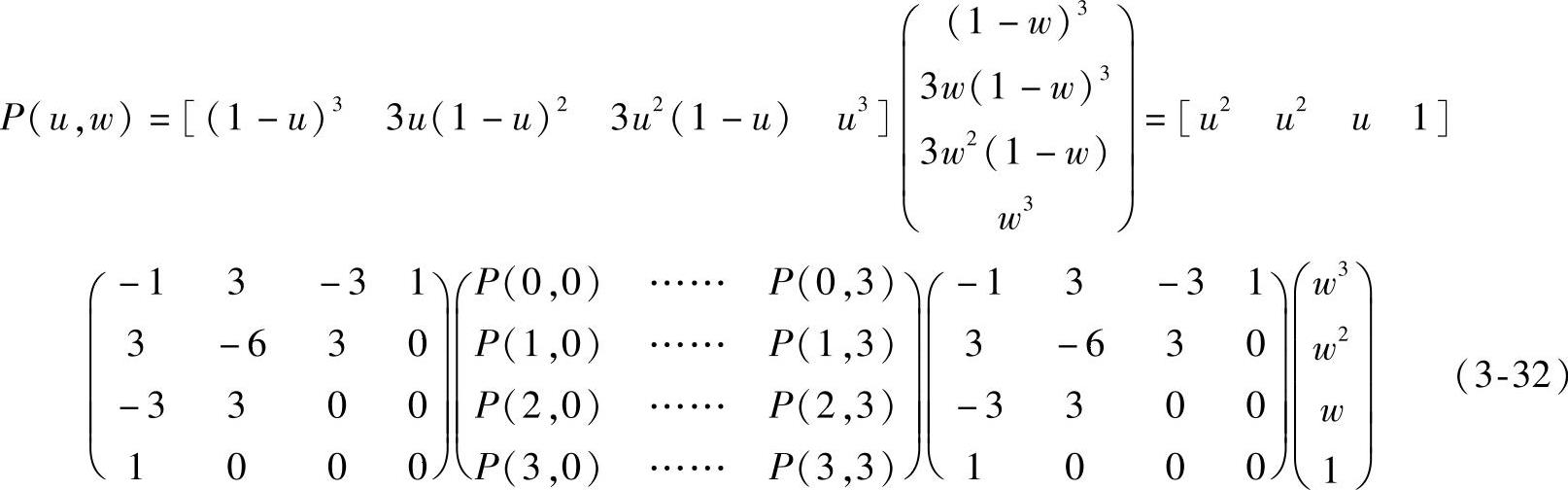
下面仍以孔斯曲面已知条件为例设计贝塞尔曲面。
绘制贝塞尔曲面的程序LP3-43.lsp可通过扫描二维码观看，图3-58所示为程序运行后所画的贝赛尔曲面。
LP3-43.lsp程序
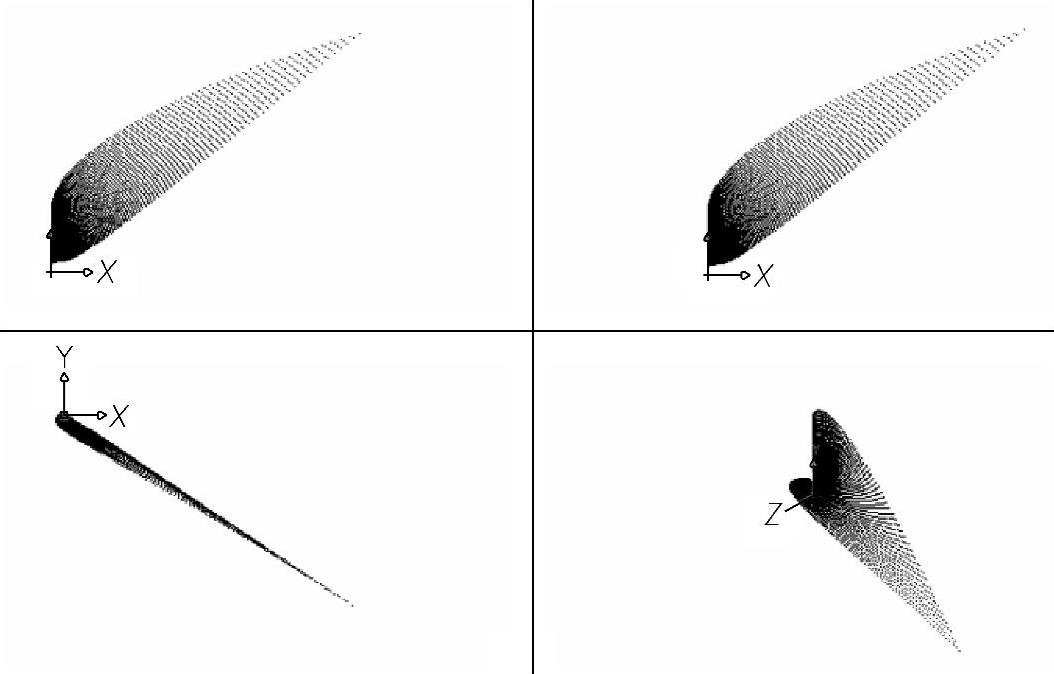
图3-58 贝塞尔曲面
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
