孔斯曲面构造方法及示例

1964年孔斯提出了一种构造曲面的数学方法。孔斯方法的基本思想是，把一个复杂的曲面看做是由若干个曲面片光滑拼接而成的，每一个曲面片都用一个数学方程式来描述。设计曲面从单个曲面片开始，在曲面片之间相邻的边界上使得位置、斜率、曲率连续，以保证整个曲面光滑连续性。

双三次曲面是由给定的两对边界曲线P（u，0）、P（u，1）、P（0，w）、P（1，w）及四个基函数混合起来生成的一个曲面片。四个基函数都是三次函数，定义如下：

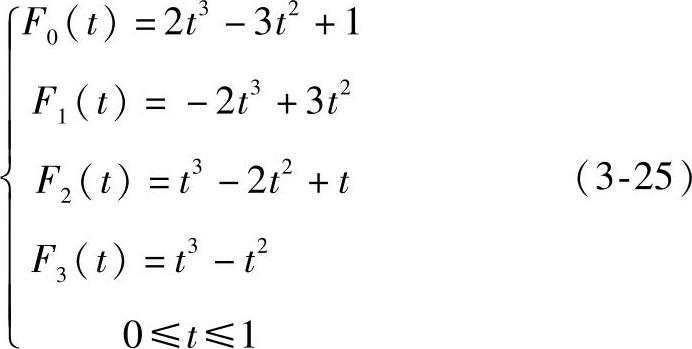
并定义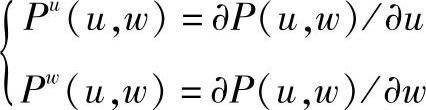为切线矢量，定义P^uw（u，w）=∂P（u，w）/∂u∂w为扭曲矢量。

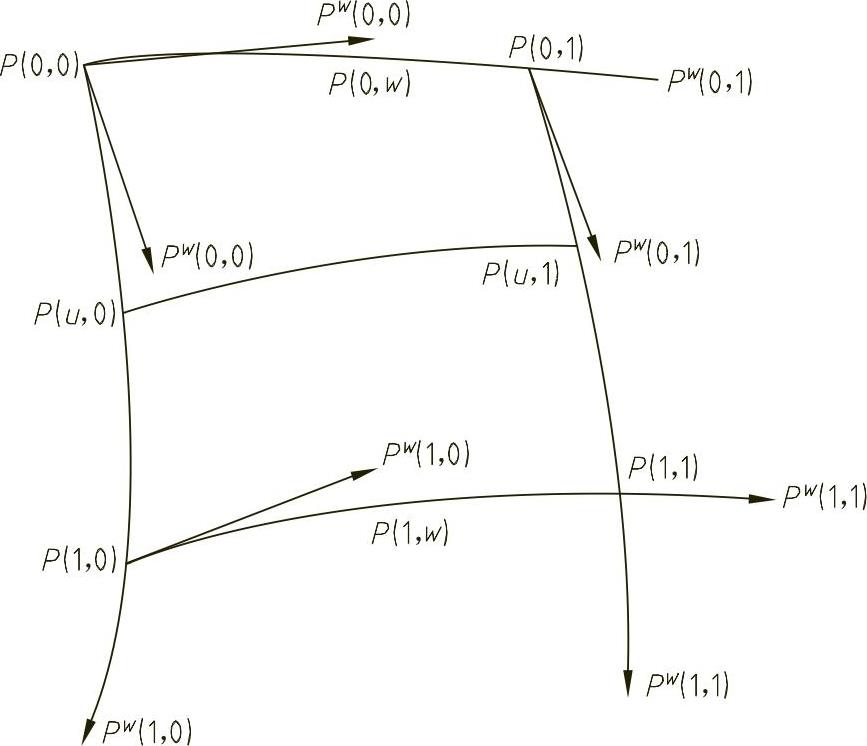
图3-55 曲面片各角点的信息

图3-55所示为各角点的位置矢量和切线矢量，这些矢量均是已知量。这样，双三次曲面片的方程式可写为

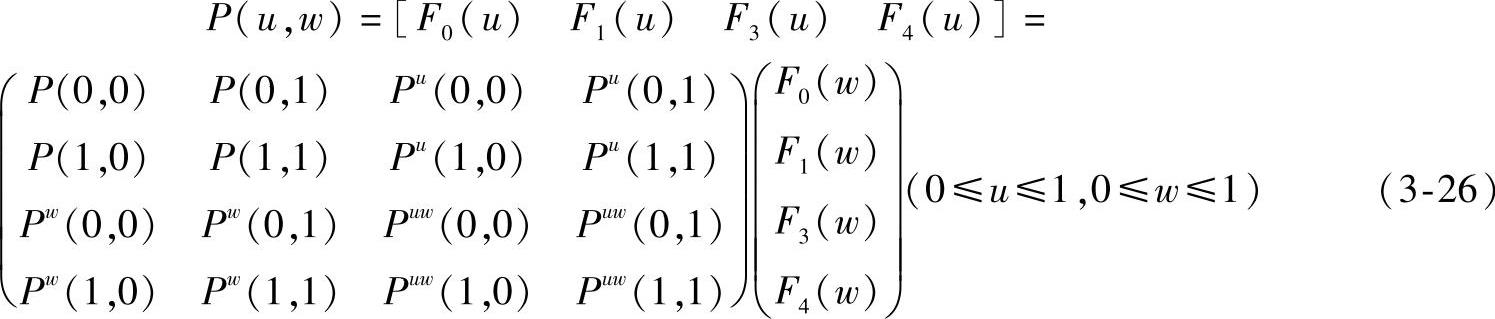
四阶方阵P中左上角的二阶方阵是角点位置，右下角二阶方阵是角点的扭曲矢量，其余两个方阵是角点沿u、w方向的切线矢量。

设平面上有四点P₀、P₁、P₂、P₃，它们的位置矢量分别为（0，0，0），（0，0.75，0），（0.75，0，0），（0.75，0.75，0），求该四点的切线矢量、跨界切线矢量和扭曲矢量。定义在关于角点的信息的矩阵M中(www.xing528.com)

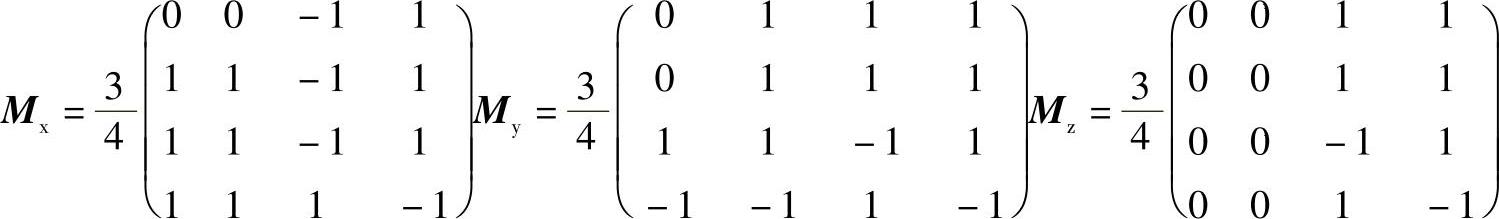
将已知条件代入式（3-26），有

绘制孔斯曲面的程序LP3-42.lsp可通过扫描二维码观看。图3-56所示为程序运行后所画的孔斯曲面。

LP3-42.lsp程序

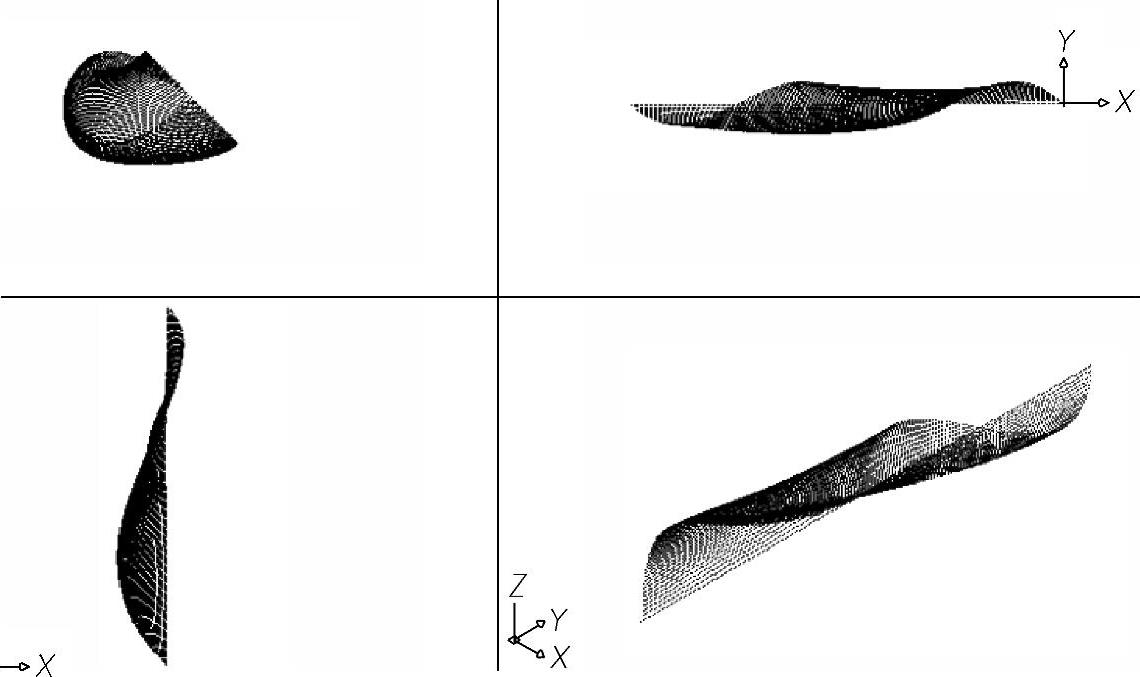
图3-56 孔斯曲面