三次B样条曲线实现-计算机实验工程图形学.下册

1.三次B样条曲线表达式

当n=3，i=0，1，2，3时，经计算整理得

F_0，3f（t）=1/6（-t³+3t²-3t+1）

F_1，3（t）=1/6（3t³-6t²+4）

F_2，3（t）=1/6（-3t³+3t²+3t+1）

F_3，3（t）=1/6t³

这样，三次B样条曲线的矩阵表达式可写为

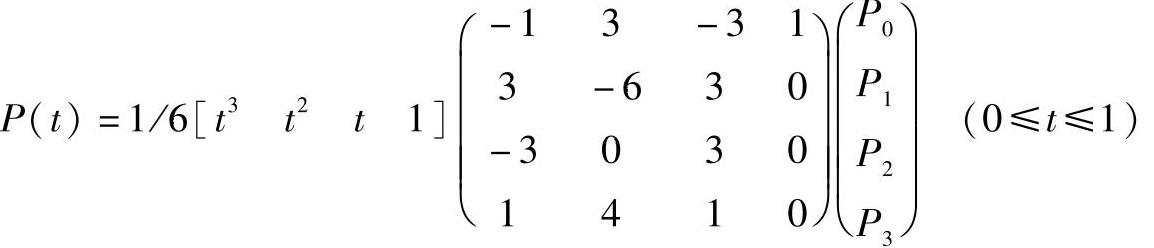
若将P₀、P₁、P₂、P₃分解为二维平面上的X、Y分量，则

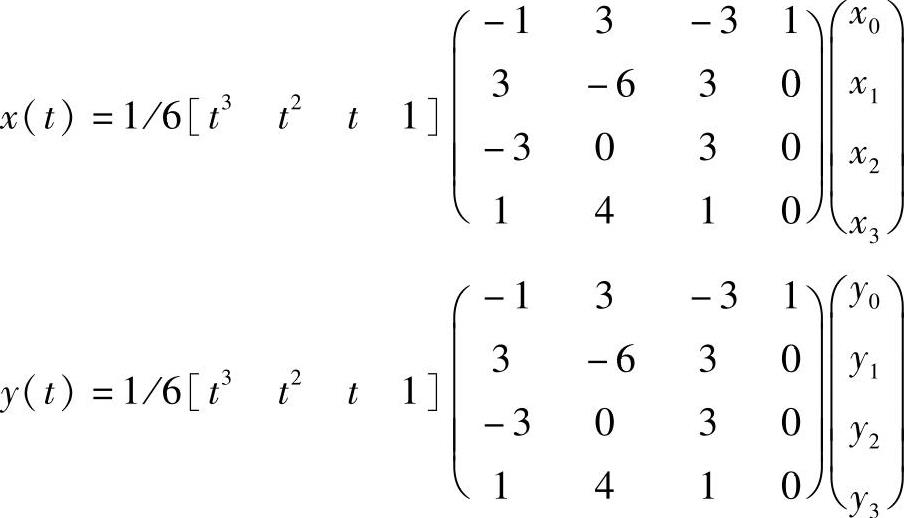
将其展开，按t的升幂书写，得三次B样条曲线的表达式为

x（t）=a₀+a₁t+a₂t²+a₃t³

y（t）=b₀+b₁t+b₂t²+bt³

式中 a₀=（x₀+4x₁+x₂）/6

a₁=（x₂-x₀）/2

a₂=（x₀-2x₁+x₂）/2

a₃=（3x₁+x₃-x₀-3x₂）/2

b₀=（y₀+4y₁+y₂）/6

b₁=（y₂-y₀）/2

b₂=（y₀-2y₁+y₂）/2

b₃=（3y₁+y₃-y₀-3y₂）/2

三次B样条曲线的端点具有如下一些性质：

P（0）=1/6（P₀+4P₁+P₂）(www.xing528.com)

P（1）=1/6（P₁+4P₂+P₃）

P′（0）=1/2（P₂-P₀）

P′（1）=1/2（P₃-P₁）

P（0）=P₀-2P₁+P₂

P″（1）=P₁-2P₂+P3

如图2-68所示，三次B样条曲线的起点P（0）位于△b₀b₁b₂的中线b₁b^*1上距点b₁的1/3处，起点的切向矢量P^*（0）平行于b₀b₂，长度为其一半。曲线的终点性质与起点性质类似。

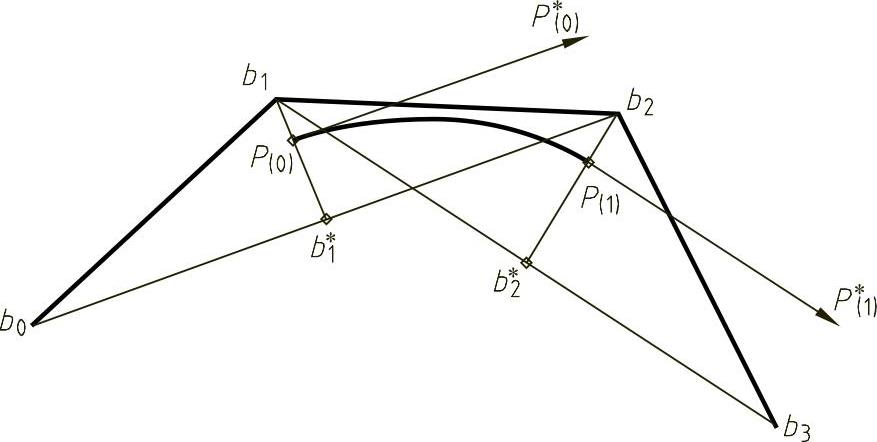
图2-68 三次B样条曲线的端点

2.三次B样条曲线的边界条件

在一些实际问题中，常常希望所设计的三次B样条曲线在给定的点上开始或终止，而且带有确定的切向矢量，也就是说在边界上满足插值条件而其余仍是逼近。假如给定B特征多边形的顶点P_i（i=0，1，…，n），希望相应的B样条曲线以P₀为起点且切于P₀P₁、以P_n为终点且切于P_n-1P_n，则只要在首末两端各延长一个顶点P_-1、P_n+1，使得

P_-1P₀=P₀P₁

P_n-1P_n=P_nP_n+1

取P_i（i=0，1，…，n，n+1）作为B特征多边形的顶点，由此生成的B样条曲线就是满足边界条件的曲线，如图2-69所示。

3.三次B样条曲线的程序设计

设四点坐标分别为：P₀（x₀，y₀），P₁（x₁，y₁），P₂（x₂，y₂），P₃（x₃，y₃），绘制一条三次B样条曲线的程序LP2-35.lsp可通过扫描二维码观看。

图2-70所示为计算机绘制的三次B样条曲线。

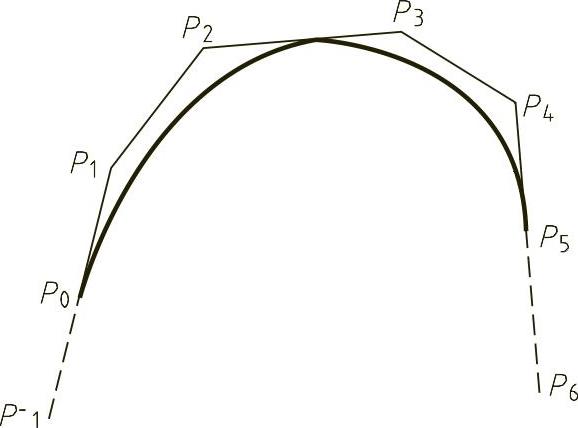
图2-69 满足边界条件的曲线

LP2-35.lsp程序

图2-70 三次B样条曲线