【摘要】:三次样条插值曲线的原理如图2-61所示。设有离散点P0,P1,…,Pn,若有一条曲线P满足:①顺次经过点Pi(i=0,1,…图2-61 三次样条插值曲线的原理以t为参数表示的单参数三次曲线可表示为每段三次样条曲线都是由其起始点的位置矢量P0、P1和起始点处的切向矢量P0′、P′1来确定的。从上面的讨论中可以看出,曲线的形状是受曲线段两端点的位置矢量和切向矢量控制的,当端点的边界条件发生变化时,曲线的形状随之改变。
三次样条插值曲线的原理如图2-61所示。
设有离散点P0(x0y0),P1(x1y1),…,Pn(xnyn),若有一条曲线P(t)满足:①顺次经过点Pi(i=0,1,…,n);②在每两个点Pi,Pi+1(i=0,1,…,n-1)之间是三次参数曲线;③整段曲线是二阶连续的,则称曲线P(t)为三次参数样条曲线。
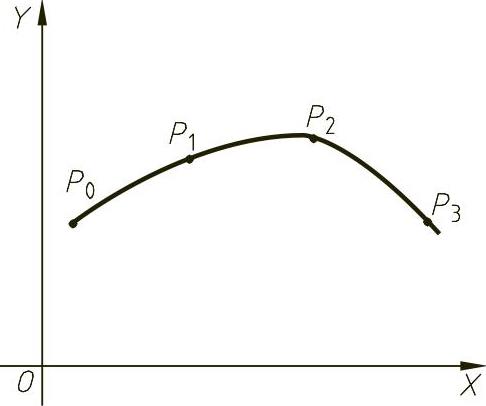
图2-61 三次样条插值曲线的原理
以t为参数表示的单参数三次曲线可表示为
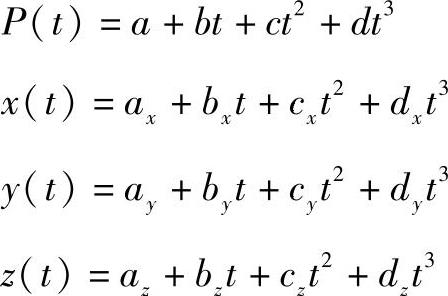
每段三次样条曲线都是由其起始点的位置矢量P0、P1和起始点处的切向矢量P0′、P′1来确定的。为叙述方便,只讨论P(t)的一个分量x(t),将x(t)的三次参数多项式用矩阵形式表示,则有
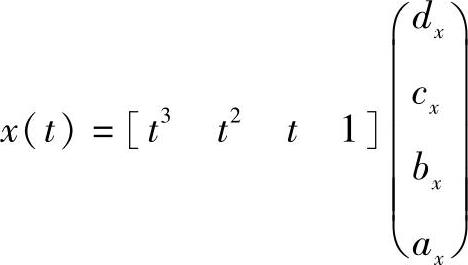
根据起始点、终止点条件,x(0)、x(1)、x′(0)、x′(1)的矩阵表达形式为
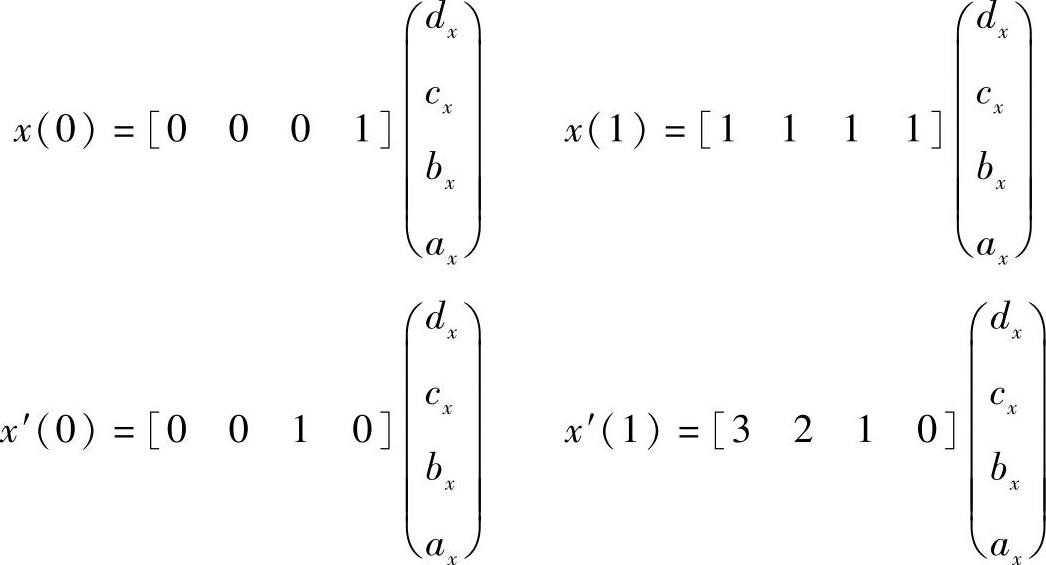
上式可综合写为
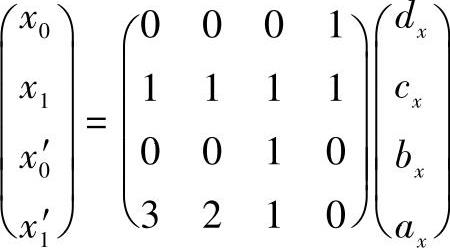
从中解出

由此可得(https://www.xing528.com)
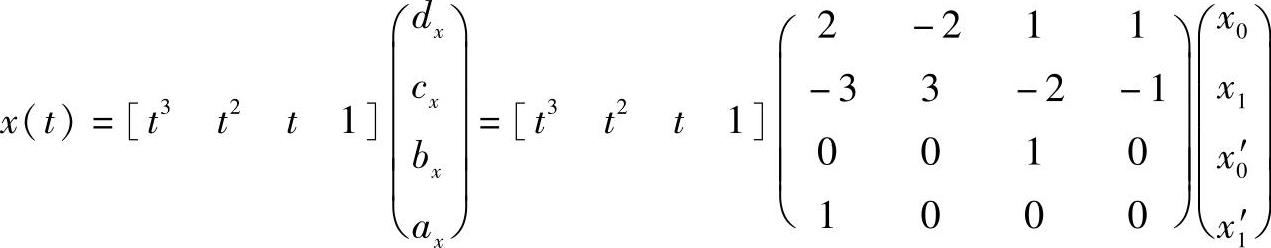
同理
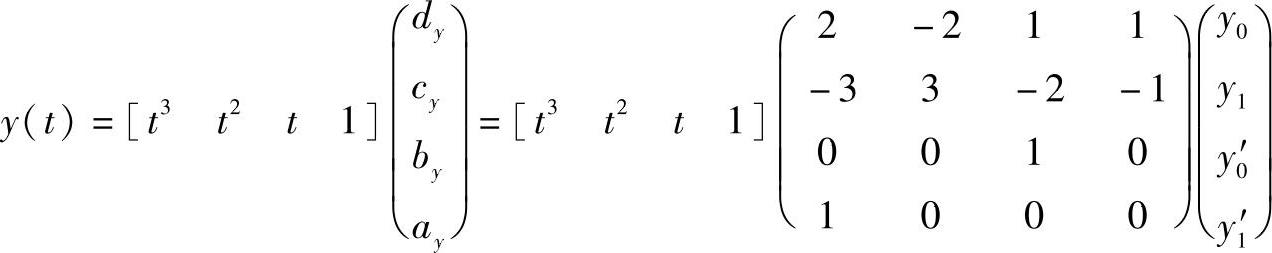
若令
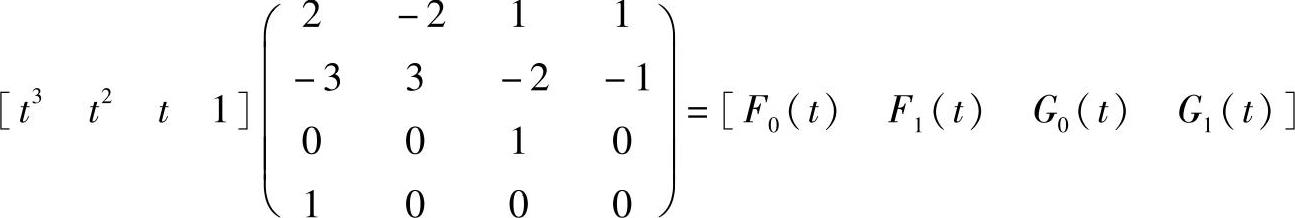
则有
F0(t)=2t3-3t2+1
F1(t)=-2t3+3t2
G0(t)=t(t-1)2
G1(t)=t2(t-1)
这组函数被称为混合函数。从上面的讨论中可以看出,曲线的形状是受曲线段两端点的位置矢量和切向矢量控制的,当端点的边界条件发生变化时,曲线的形状随之改变。
由方程可知,在已知两端点区间内的插值点坐标为
x(t)=(2t3-3t2+1)x0+(-2t3+3t2)x1+(t3-2t2+t)x0′+(t3-t2)x1′
y(t)=(2t3-3t2+1)y0+(-2t3+3t2)y1+(t3-2t2+t)y0′+(t3-t2)y1′
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




