质点的直线运动是指质点沿一条直线运动。在任意时刻t,质点都会对应直线上的某一确定位置。质点的直线运动可以用图示的方法表达其位置、速度和加速度。
假设作直线运动的质点,它的位置满足方程
x=6t2-t3 (2-17)
式(2-17)中,t的单位是s,x的单位是m。将x对时间t求导,就得到了质点在任意时刻t的速度

再求一次导,就得到了加速度a的表达式

根据式(2-17)、式(2-18)、式(2-19)编写程序:
(1)质点运动位置与时间的程序

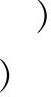
程序运行结果如图2-54所示。
(2)质点运动速度与时间的程序

程序运行结果如图2-55所示。
(3)质点运动加速度与时间的程序

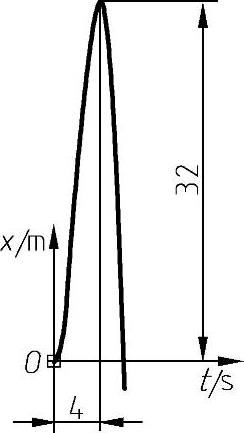
图2-54 质点运动位置与时间的关系
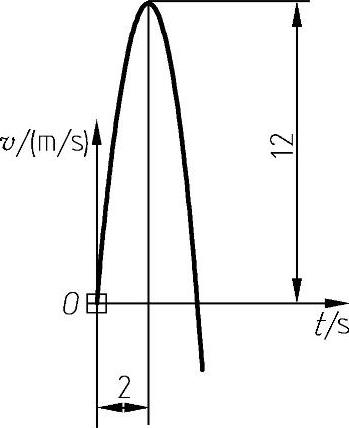
图2-55 质点运动速度与时间的关系
程序运行结果如图2-56所示。
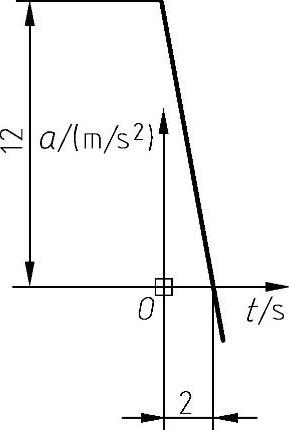
图2-56 质点运动加速度与时间的关系
上述位置、速度、加速度都是相对于时间t的变化图形,这些曲线就是所谓的运动曲线。根据这些图形,可以查询某一时刻点的运动位置、运动速度和运动加速度。但是一定要注意,质点不沿其中任何一条曲线运动,而是在直线上运动。由于函数的导数就是函数曲线的斜率,所以曲线x-t每一时刻的斜率就等于该时刻v的大小,同样,曲线v-t每一时刻的斜率就等于该时刻a的大小。因此,当t=2s时,a=0,曲线v-t的斜率一定也等于零,此时速度有一个极大值。同样,当t=0s和t=4s时,v=0,曲线x-t在这两个时刻的切线一定是水平的。对以上三条曲线进行研究,可以将t=0时刻到t=∞质点的运动分成四个阶段:
1)质点从原点x=0处开始运动,初速度为零,但是加速度不为零且是正的。在这种情况下,质点会得到一个正的速度,并且沿正方向移动。从t=0到t=2s,x、v和a都是正的。
2)t=2s时,加速度为零,速度达到最大值。从t=2s到t=4s,v是正的,但a是负的,质点仍然沿正方向运动,但是越来越慢,质点正在减速。
3)t=4s时,速度为零,位置坐标x达到最大值。从此v和a就为负,质点正在沿负方向加速运动,速度不断增加。
4)t=6s,质点通过原点,它的位置坐标为零,同时从开始到此刻质点运动的路程的长度为64m。当t=6s以后,x、v和a都是负的。质点继续沿负方向前进,并且越来越快。从上面的讨论可以看出,如果知道了质点在每一时刻t的位置,就认为质点的运动已知。而通常情况下,运动很少由x和t的关系决定,更多是由质点的加速度形式给出的。
例2-1 如图2-57a所示,一个小球从一个距离地面20m的窗口,以10m/s的速度铅垂向上运动,已知小球的加速度是常数,值为9.81m/s2,方向竖直向下。求:(1)任意时刻小球的速度v和高度y;(2)小球达到最高点的时间及高度;(3)小球落地的时刻及相应的运动速度;(4)画出v-t、y-t曲线。
解 (1)速度和高度 表示小球位置坐标的Y轴原点选择在地面上,正方向向上。加速度的值v和y初值如图2-57a所示。将a代入a=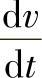 中,并注意到t=0时v=+10m/s,有
中,并注意到t=0时v=+10m/s,有
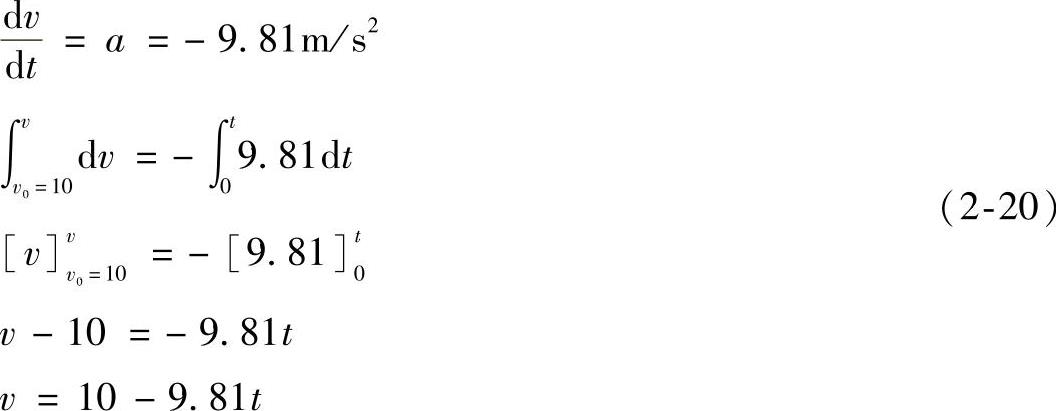
将v代入v=dy/dt,并注意到t=0时y0=20m,从而得到
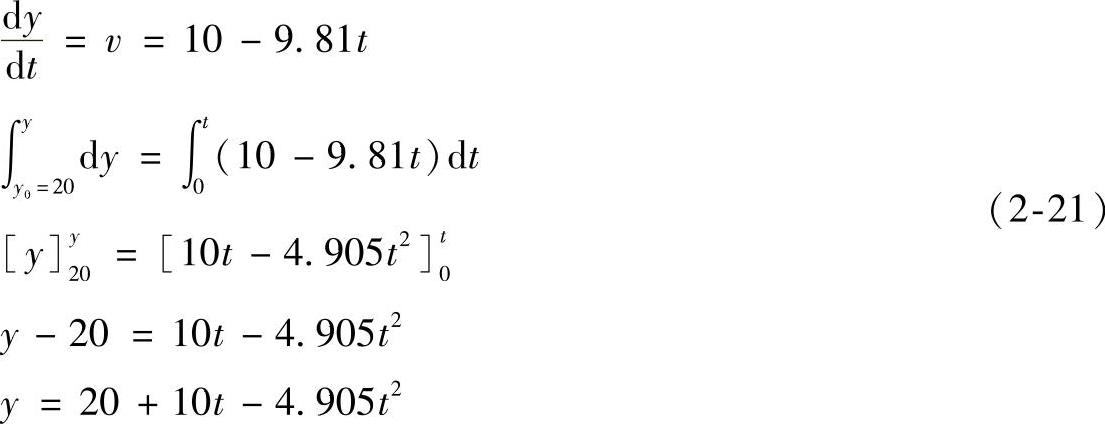
(2)最高点 当小球达到最高点时,v=0,代入式(2-20)得10-9.81t=0,即t=1.019s。将t=1.019s代入式(2-21)中得y=20+10(1.019)-4.095(1.019)2,即y=25.1m。
(3)球落地 当球落地时,将y=0代入式(2-21)中,得20+10t-4.905t2=0,即t=-1.243s或t=+3.28s。只有根t=+3.28s符合运动开始后的条件。将其代入式(2-20),得(https://www.xing528.com)
v=(10-9.81×3.28)m/s=-22.2m/s
即球落地时速度为22.2m/s,方向向下。
(4)画v-t曲线


程序运行后得到速度与时间的关系曲线,如图2-57b所示。画y-t曲线

程序运行后得到高度与时间的关系曲线,如图2-57c所示。
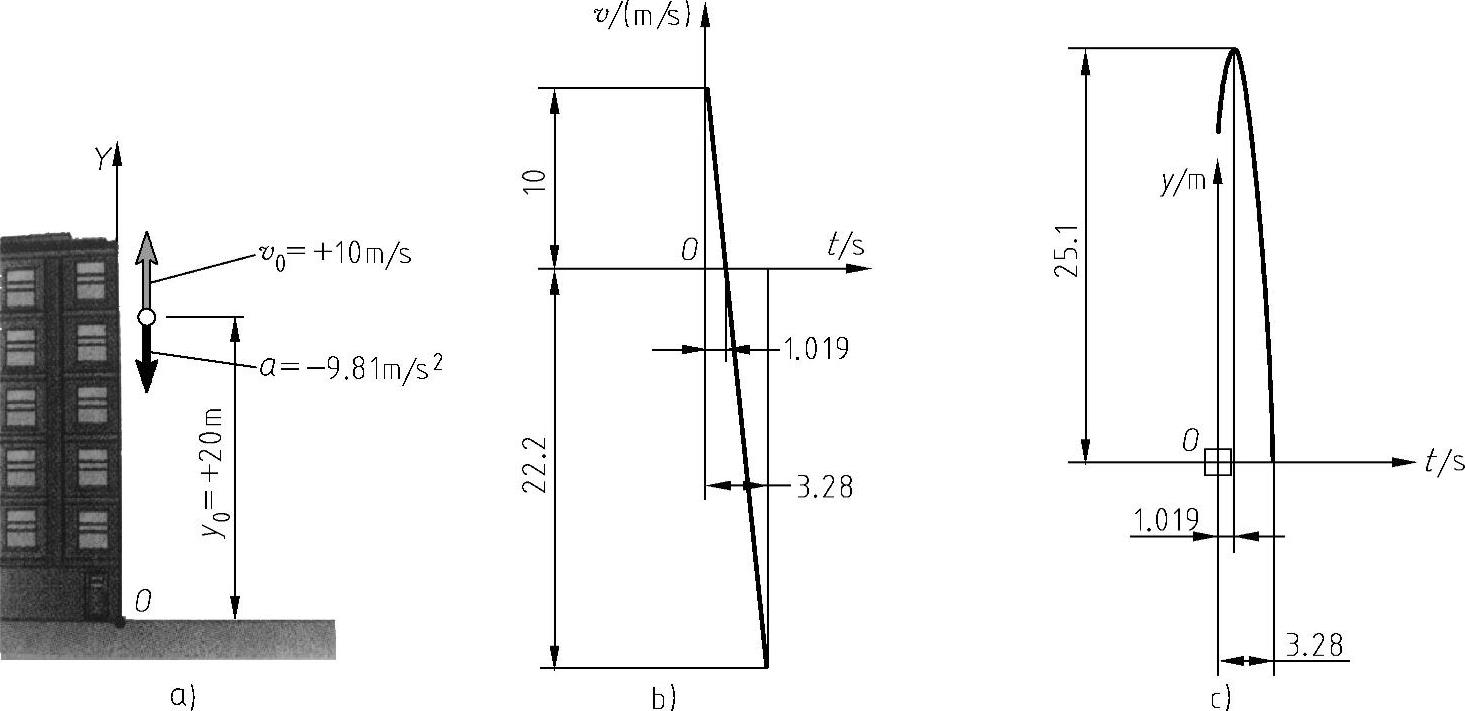
图2-57 小球的运动
a)已知条件 b)v-t曲线 c)y-t曲线
例2-2 图2-58a所示的减振机构通常用在枪械上以减小反冲力,它主要是由一个连接着枪炮的活塞和一个充满油的刚性液压缸组成,活塞在液压缸中往复运动。当炮管以初速度v0产生一个反冲力时,活塞运动,油被压进活塞上的小孔,这样炮管和活塞一起按照与其速度成正比的比例减速,即a=-kv。(1)将v表示成时间t的函数;(2)将x表示成时间t的函数;(3)将v表示成位置坐标x的函数,并画出相应的曲线。
解 (1)将v表示成时间t的函数 将a=-kv代入基本的加速度公式a=dv/dt中,得

(2)将x表示成时间t的函数 将刚才得到的表达式代入v=dx/dt得
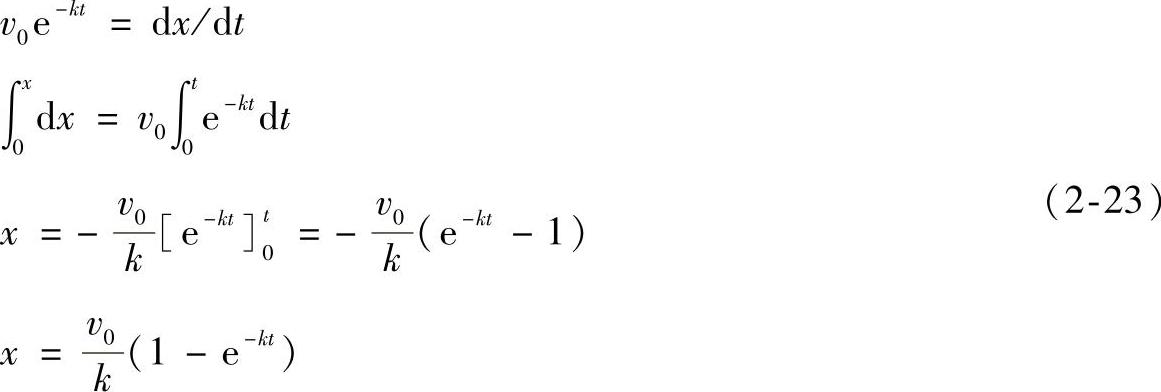
(3)将v表示成位置坐标x的函数。将a=-kv代入a=vdv/dx得

根据式(2-22)编写v-t曲线程序如下:

运行程序可得v-t曲线,如图2-58所示。根据式(2-23)编写x-t曲线程序如下:
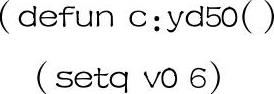

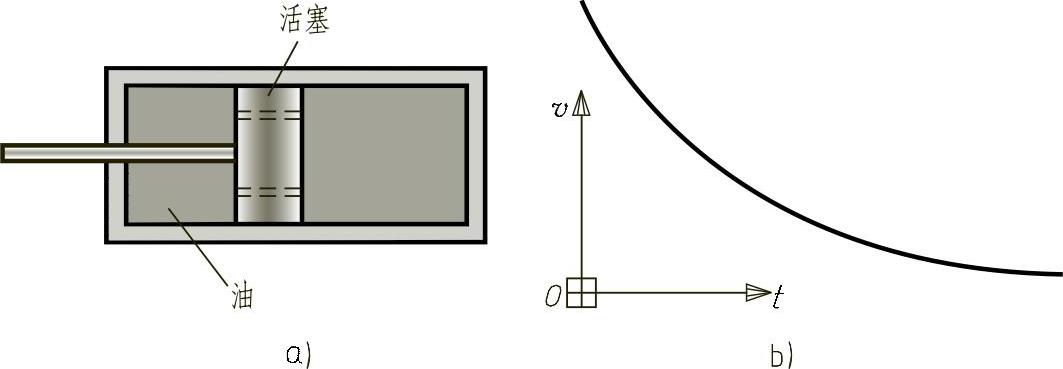
图2-58 减振机构及v-t曲线
a)减振机构 b)v-t曲线
运行程序可得x-t曲线,如图2-59所示。
根据式(2-24)编写v-x曲线程序如下:

运行程序可得v-x曲线,如图2-60所示。
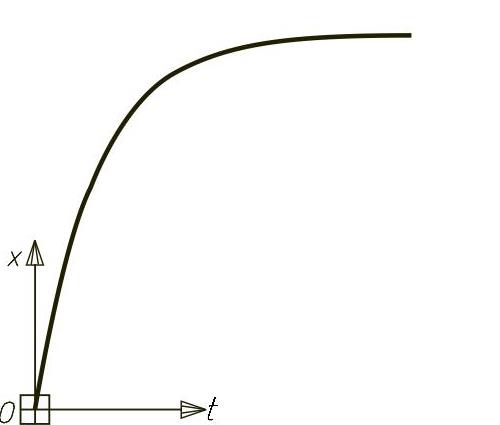
图2-59 x-t曲线
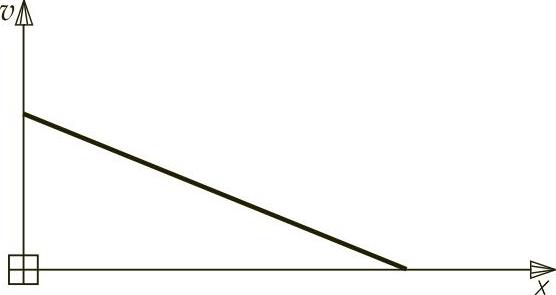
图2-60 v-x曲线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




