计算机实验工程图形学下册-圆柱螺旋线

1.圆柱螺旋线的几何模型

一个动点顺着正圆柱面上的直母线作等速运动，而母线又同时绕着圆柱轴线作等角速旋转运动，则该动点在圆柱表面上所形成的轨迹称为圆柱螺旋线，如图2-27所示。按螺旋线形成规律，当直母线旋转一周，点沿着轴线方向上升（或下降）的距离称为导程T，在同一个圆柱面上，只要改变动点沿直母线移动的速度或直母线绕轴线旋转的角速度，就可以得到不同导程的螺旋线。

2.圆柱螺旋线的数学模型

设螺旋线所在圆柱面的半径为r，直母线绕轴线旋转的角速度为ω，动点A沿直母线运动的线速度为v。以时间t为参数，设t=0时动点在X轴上A₀（r，0，0）位置。经时间t后，动点转到A（x，y，z）处。这时动点A一方面绕轴线转过了θ=ωt角，另一方面沿直母线上升了相应的高度h=vt。所以螺旋线的参数方程为

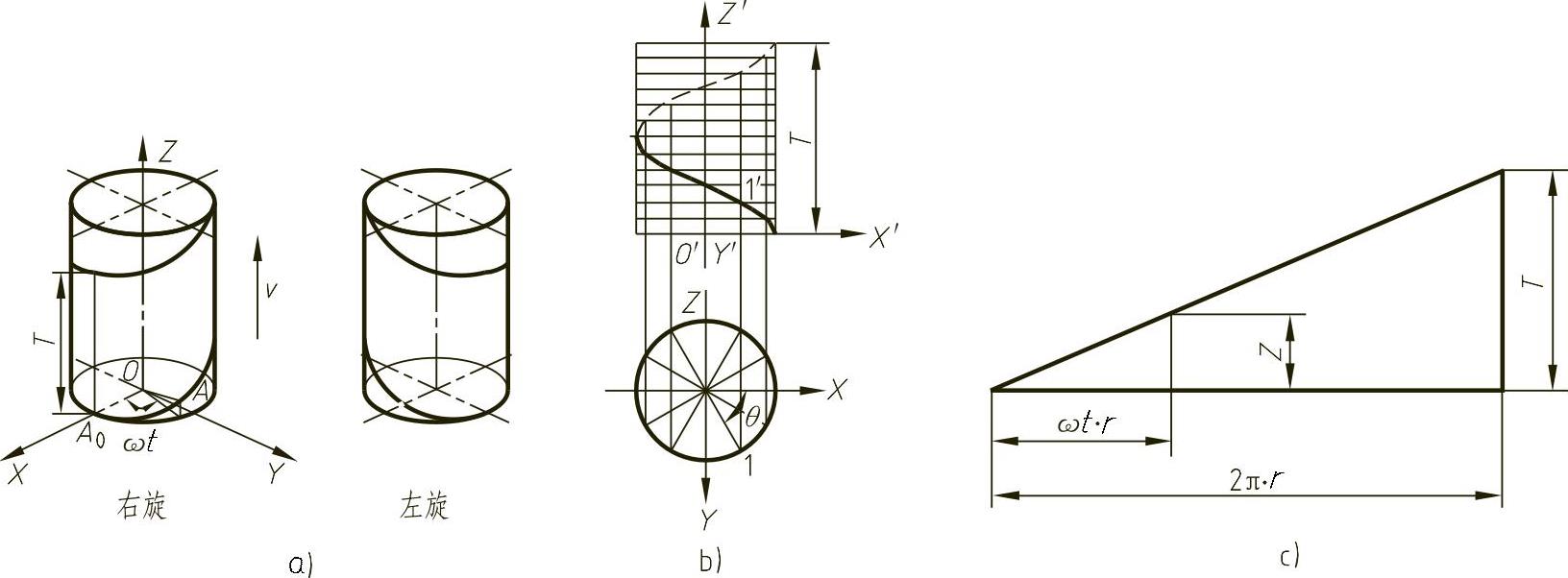
图2-27 圆柱螺旋线

a）圆柱螺旋线直观图 b）圆柱螺旋线投影图 c）圆柱螺旋线展开图

因为θ=ωt，由图2-27b可知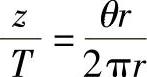，，所以式（2-8）也可写成

(www.xing528.com)

式（2-9）就是一般的圆柱螺旋线的参数方程。

3.圆柱螺旋线的程序设计

圆柱螺旋线的程序LP2-19.lsp、LP2-20.lsp两种设计方式，可分别通过扫描相应二维码观看。运行程序后所得到的图形如图2-28a、b所示。

LP2-19.lsp程序

LP2-20.lsp程序

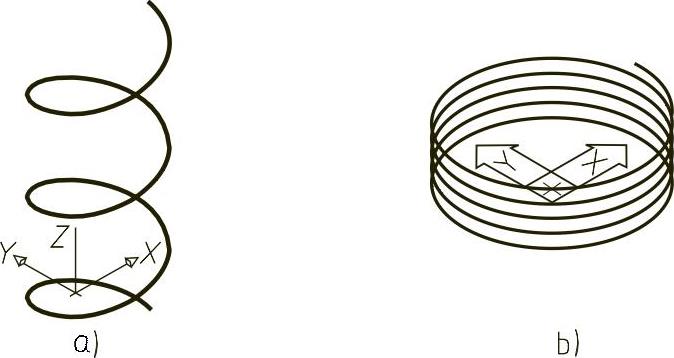
图2-28 计算机绘制的圆柱螺旋线