快速构建观察模型：旋转变换方法

换面法是物体不动，而变换投影面使其处于能表达物体表面实形的位置，或使几何元素的新投影处于有利于解题的位置。这一结果也可以用另一种方法得到，如图1-62所示。

图1-61 凹槽块主、俯视图

表1-4 各投射方向下的立体感图形

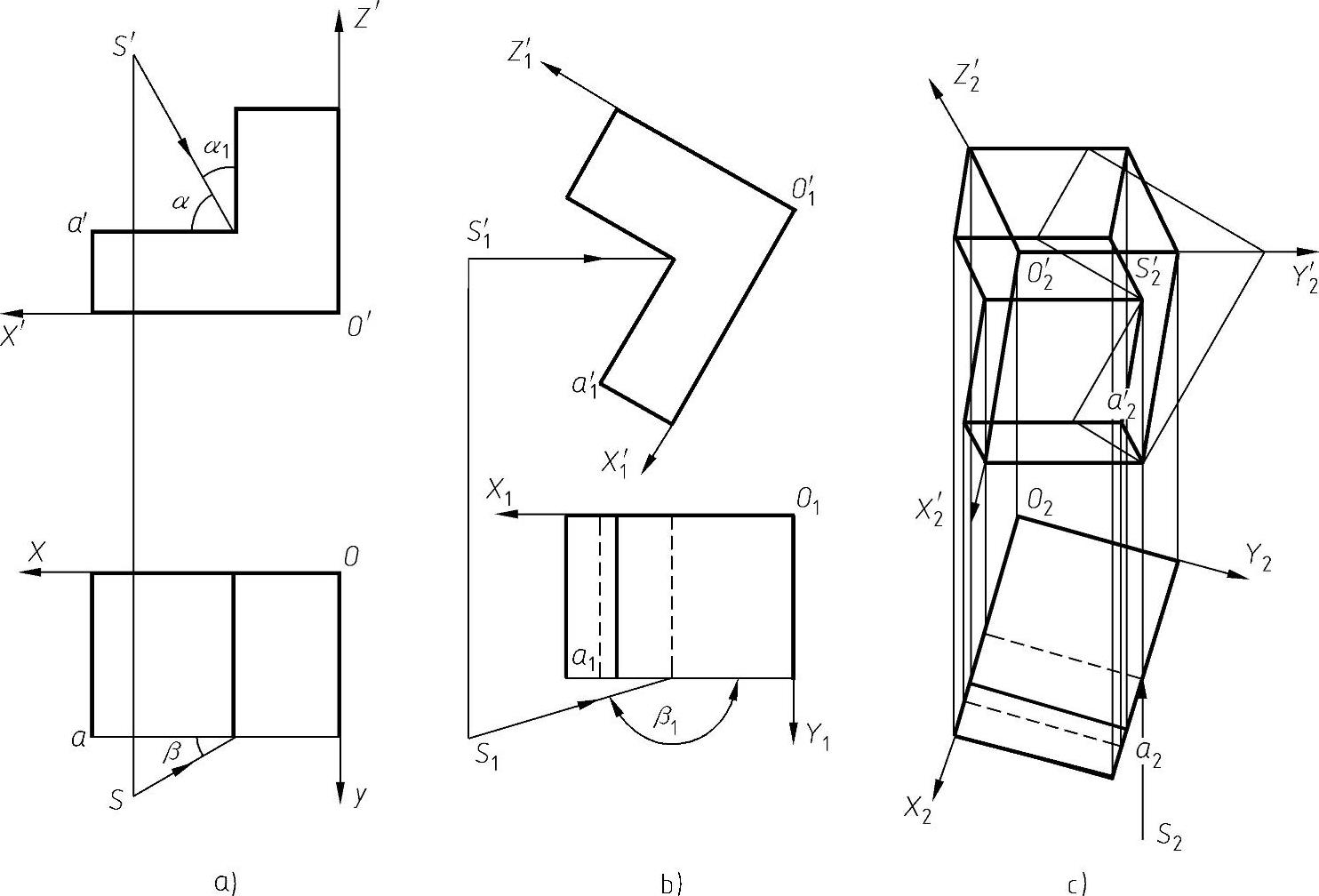
图1-62 旋转物体使投影有立体感

设投影面不动，将投射方向连同物体先绕Y轴旋转α角，如图1-62a所示。此时，投射方向变成水平线。再绕Z轴旋转β₁角，如图1-62b所示。此时，投射方向变成正垂线。物体的正面投影就有了立体感，如图1-62c所示。根据坐标轴的旋转，设图1-62中物体连同确定物体的坐标轴先绕Y轴旋转α角，再绕Z轴旋转β₁角，然后用投射法向投影面V进行投射，这时，三个坐标面对投影面V都不平行，在该投影面上反映出了物体上各点的新坐标（x₂，y₂，z₂）[如A点的新坐标，A₂（x₂，y₂，z₂）]后，即可在V投影面上可画出有立体感的图形。为了推导出V面上反映三维空间图形的坐标变换关系，先建立绕坐标轴旋转的关系式。取任意一点O₁（a，b，c）建立新坐标系O₁X₁Y₁Z₁，使各坐标轴与原坐标系OXYZ中的对应坐标轴互相平行，且同向。为简便起见，常使O₁与O点重合，如图1-63a所示。当O₁X₁Z₁坐标面绕O₁Y₁轴逆时针方向旋转某一θ角时，原坐标系OXYZ中一点M（x，y，z）与它在新坐标系O₁X₁Y₁Z₁中的坐标M₁（x₁，y₁，z₁）的关系为

写成矩阵积的形式为

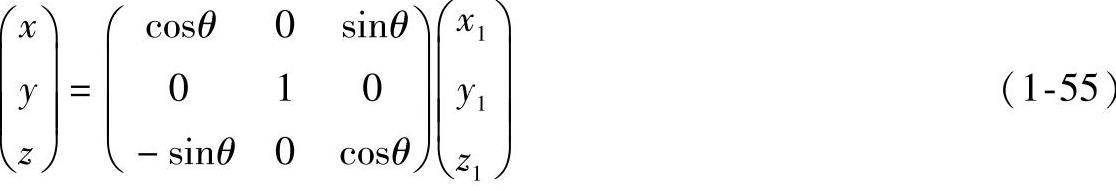
或简写成

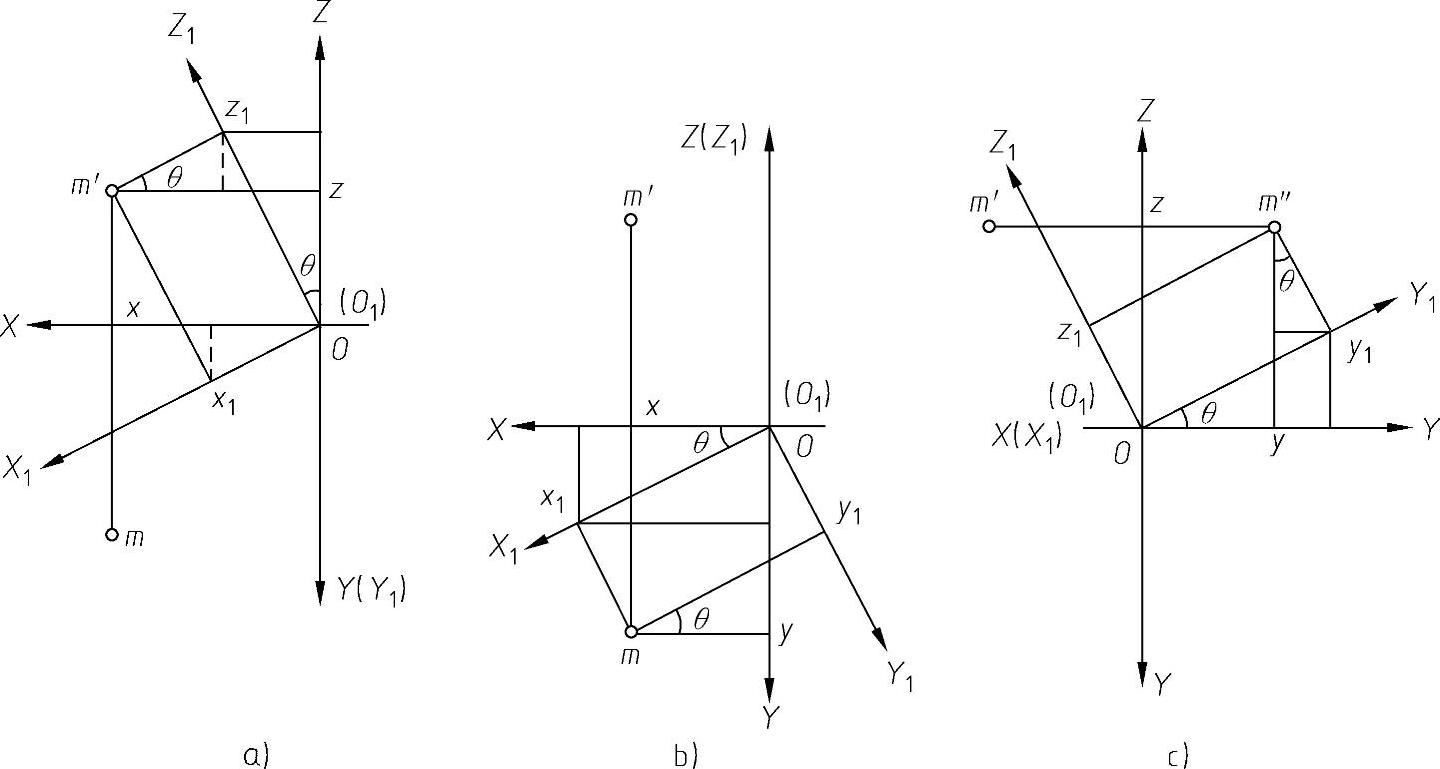
图1-63 点绕坐标轴旋转

分别绕O₁Z₁、O₁X₁轴旋转（见图1-63b、c），也有类似的变换公式。绕O₁Z₁旋转

写成矩阵积的形式为

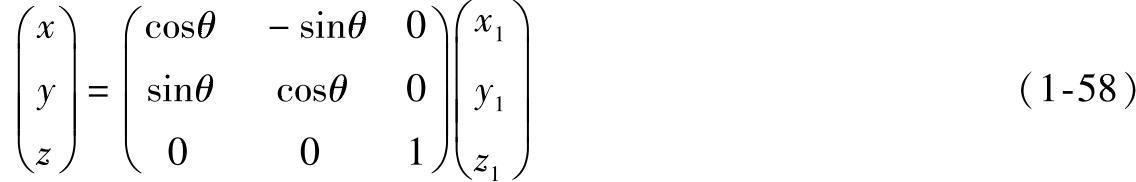
或简写成

(www.xing528.com)

绕O₁X₁旋转

写成矩阵积的形式为

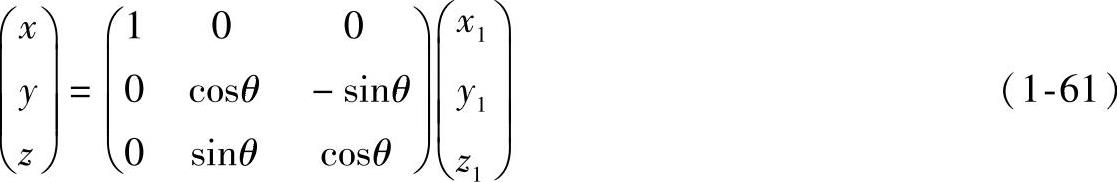
或简写成

根据坐标轴的旋转，设图1-63中物体上一点A（x、y、z）先绕Y轴旋转α角，再绕Z轴旋转β₁角后得到A₂（x₂，y₂，z₂），用旋转矢量表示

写成矩阵形式为

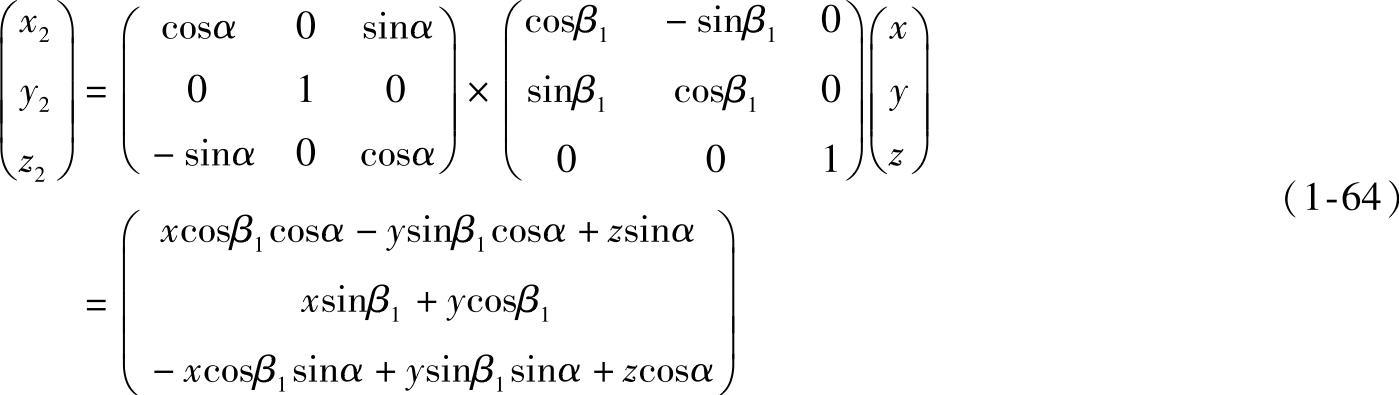
在平面上用坐标法绘制三维空间的立体感图形时，常取此式中的y₂、z₂分量坐标即

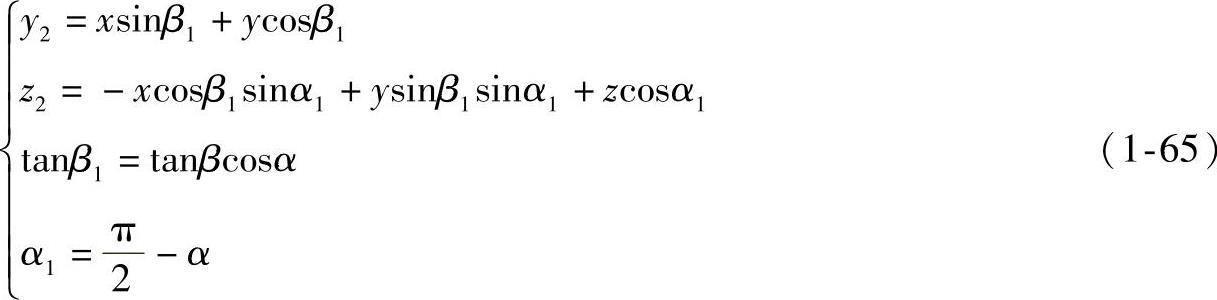
写成矩阵形式为

在这里，二行三列矩阵是从三维变换成二维的矩阵。它不是正方矩阵，因此，也不存在逆矩阵（因为不能够从二维变换成三维，用一个二维图形来表达三维图形是不确定的）。

根据式（1-63）～式（1-66）可以编写以α、β为参数的计算机绘图程序，即可得各观察方向下的立体感图形。如图1-64所示物体，其主、俯视图没有立体感，通过标注尺寸，建立坐标系，选择投射方向S，应用式（1-59）即可计算出物体上各点的新坐标，然后编写程序LP1-7，应用计算机可以绘制立体感图形，见表1-5。

由视图想象空间形体是非常重要的内容，虽然借助经验和书中所介绍的形体分析法、线面分析法、构形想象等都是很好的读图方法，但毕竟都是以经验为主，都是定性的方法。而由投影变换来理解空间的实验方法是一种定量的方法，得到的虽然也是投影图，但这种图形有立体感，有助于人对物体形状的理解和认识，而且因为应用计算机处理，可以得到各个方向下看到的立体感图形，有助于人对物体形状的全面理解。根据变换投影面实验和旋转物体实验用到的数学公式所编写的程序具有通用性，对不同的物体只是输入不同几何信息的区别。因此，实验的理论依据是根据投影变换和物体旋转建立起来的数学模型，实验的实现方法是将数学模型转变成计算机程序，实验条件是物体的几何信息，可以是物体各点坐标，物体各点坐标可以由物体尺寸和建立坐标系而获得，实验的结果是一系列具有立体感的投影图。根据数学模型编写绘图程序的方法的相关内容，请读者参见本书上册第6章图形参数化编程方法。表1-4、表1-5的绘图程序分别为LP1-6.lsp、LP1-7.lsp，请分别扫描二维码观看。

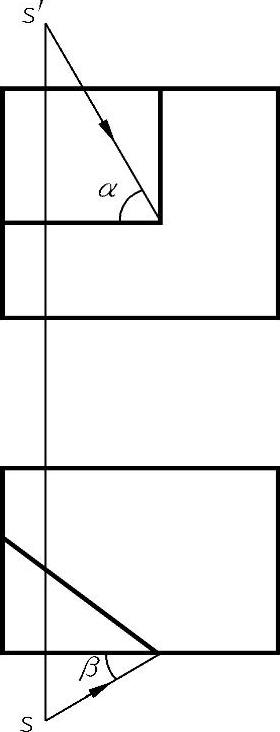
图1-64 物体的视图