在解上述各种基本度量、定位问题的过程中,有两种投影变换是基本的:一是将一般位置直线变换为投影面的垂直线;二是将一般位置平面变换为投影面的平行面。现建立这两种投影变换的数学模型。
1.一般位置直线变换成投影面的垂直线
设α0、β0为确定直线空间方位的已知参数,如图1-46所示。
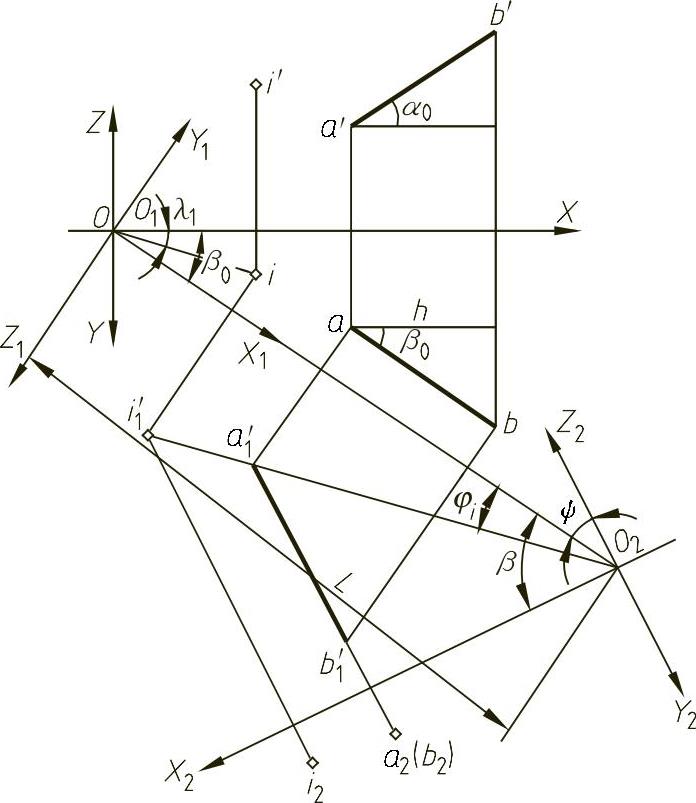
图1-46 一般位置直线的投影变换
根据投影变换的作图顺序,在相应的投影体系中建立一个坐标系与之对应。在图1-46中,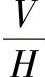 与OXYZ对应;
与OXYZ对应;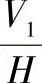 与O1X1Y1Z1对应;
与O1X1Y1Z1对应;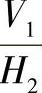 与O2X2Y2Z2对应。且使OXYZ与O1X1Y1Z1共原点,即O、O1两点重合在X轴上,而坐标系O2X2Y2Z2的原点建立在X1轴上,O2、O1相距为L。由投影变换的方法可知L的长度可以任意选取而对解题结果并无影响。将直线AB进行第二次变换时,投影体系
与O2X2Y2Z2对应。且使OXYZ与O1X1Y1Z1共原点,即O、O1两点重合在X轴上,而坐标系O2X2Y2Z2的原点建立在X1轴上,O2、O1相距为L。由投影变换的方法可知L的长度可以任意选取而对解题结果并无影响。将直线AB进行第二次变换时,投影体系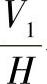 与新投影体系
与新投影体系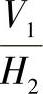 的相对位置取决于H2面和V1面的交线X2轴的位置,也即由β角确定。由此知直线AB经两次投影变换后的投影取决于β0和β角。在将一般位置直线变换为投影面的垂直线的系统中,如有一点I(xi,yi,zi)随直线AB一起变换,则Ⅰ点经一次投影变换后其在O1X1Y1Z1坐标系中的坐标为
的相对位置取决于H2面和V1面的交线X2轴的位置,也即由β角确定。由此知直线AB经两次投影变换后的投影取决于β0和β角。在将一般位置直线变换为投影面的垂直线的系统中,如有一点I(xi,yi,zi)随直线AB一起变换,则Ⅰ点经一次投影变换后其在O1X1Y1Z1坐标系中的坐标为
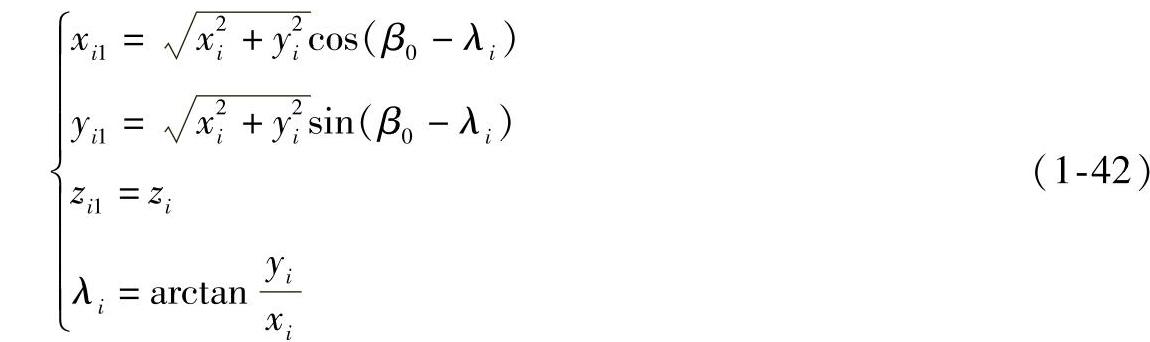
经第二次投影变换后其在O2X2Y2Z2坐标系中的坐标为
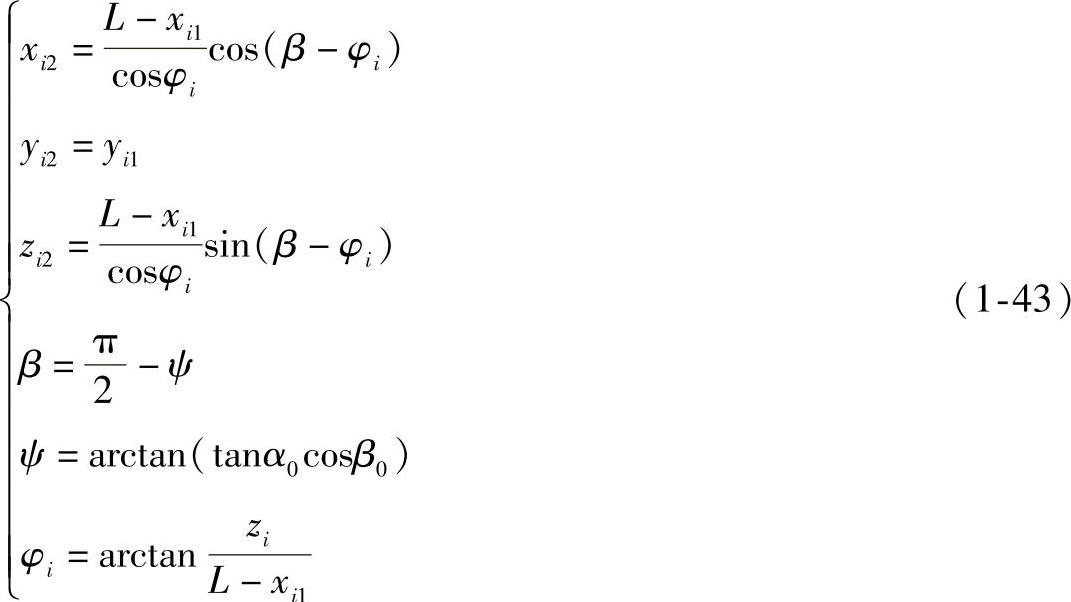
式(1-42)、式(1-43)即为一般位置直线变换为投影面垂直线的数学表达式。
2.一般位置平面变换成投影面平行面的数学模型
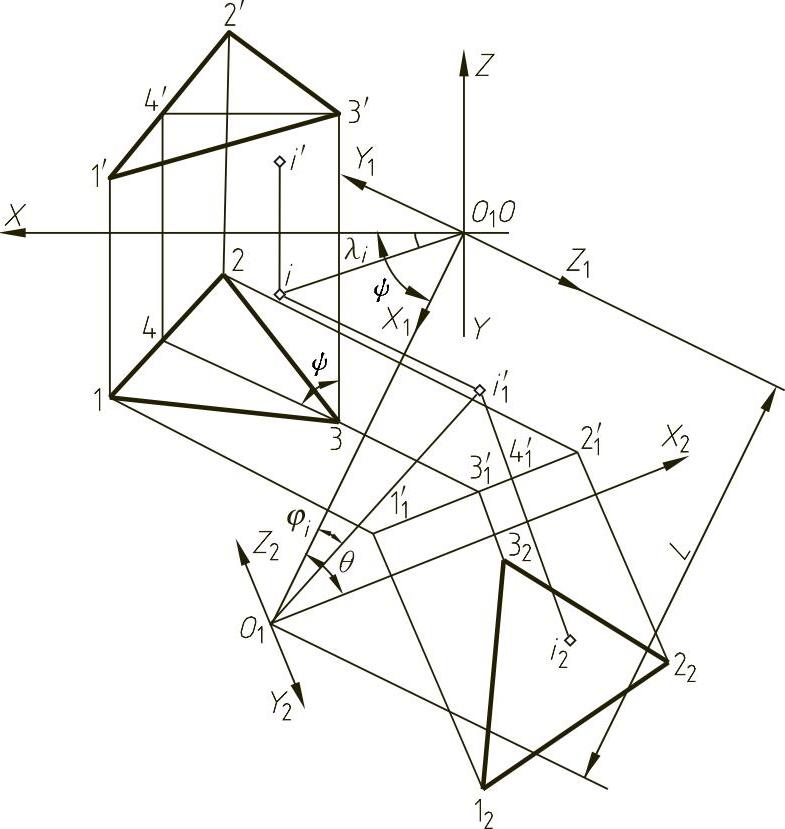
图1-47 一般位置平面变换为投影面的平行面
已知平面上三个点的坐标Ⅰ(x1,y1,z1),Ⅱ(x2,y2,z2),Ⅲ(x3,y3,z3)。将一般位置平面变换为投影面的平行面的作图顺序可参见图1-47。在相应的投影系中建立不同的坐标系与之对应,即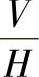 与OXYZ对应,
与OXYZ对应, 与O1X1Y1Z1对应,
与O1X1Y1Z1对应,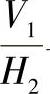 与O2X2Y2Z2对应。且使OXYZ与O1X1Y1Z1共原点,即O、O1两点重合在X轴上,而坐标系O2X2Y2Z2的原点建立在X1轴上,O2、O1相距为L。由投影变换的方法可知L的长度可以任意选取而对解题结果并无影响。将平面△ⅠⅡⅢ一次投影变换时,投影体系
与O2X2Y2Z2对应。且使OXYZ与O1X1Y1Z1共原点,即O、O1两点重合在X轴上,而坐标系O2X2Y2Z2的原点建立在X1轴上,O2、O1相距为L。由投影变换的方法可知L的长度可以任意选取而对解题结果并无影响。将平面△ⅠⅡⅢ一次投影变换时,投影体系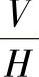 与新投影体系
与新投影体系 的相对位置取决于H面和V1面的交线X1轴的位置,也即由角ψ确定。第二次投影变换时,投影体系
的相对位置取决于H面和V1面的交线X1轴的位置,也即由角ψ确定。第二次投影变换时,投影体系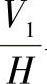 与新投影体系
与新投影体系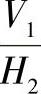 的相对位置取决于H2面和V1面的交线X2轴的位置,也即由θ角确定。由此可知,平面经两次投影变换后,其投影取决于ψ、θ角,而ψ、θ则由投影变换的目的及已知条件确定。由图1-47中一般位置平面变换成投影面的平行面的作图步骤可知
的相对位置取决于H2面和V1面的交线X2轴的位置,也即由θ角确定。由此可知,平面经两次投影变换后,其投影取决于ψ、θ角,而ψ、θ则由投影变换的目的及已知条件确定。由图1-47中一般位置平面变换成投影面的平行面的作图步骤可知

令 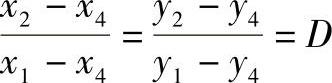
则有 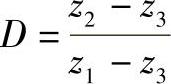
由此得 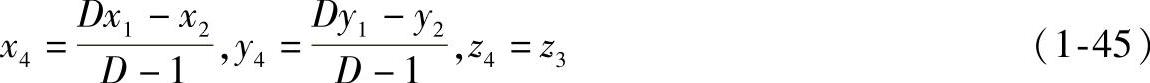

在将一般位置平面变换为投影面的平行面的体系中,如有一点Ⅰ(xi,yi,zi)随平面△ⅠⅡⅢ一起变换,则Ⅰ点经一次投影变换后,其在O1X1Y1Z1坐标系中的坐标为

Ⅰ点经第二次投影变换后,其在O2X2Y2Z2坐标系中的坐标为
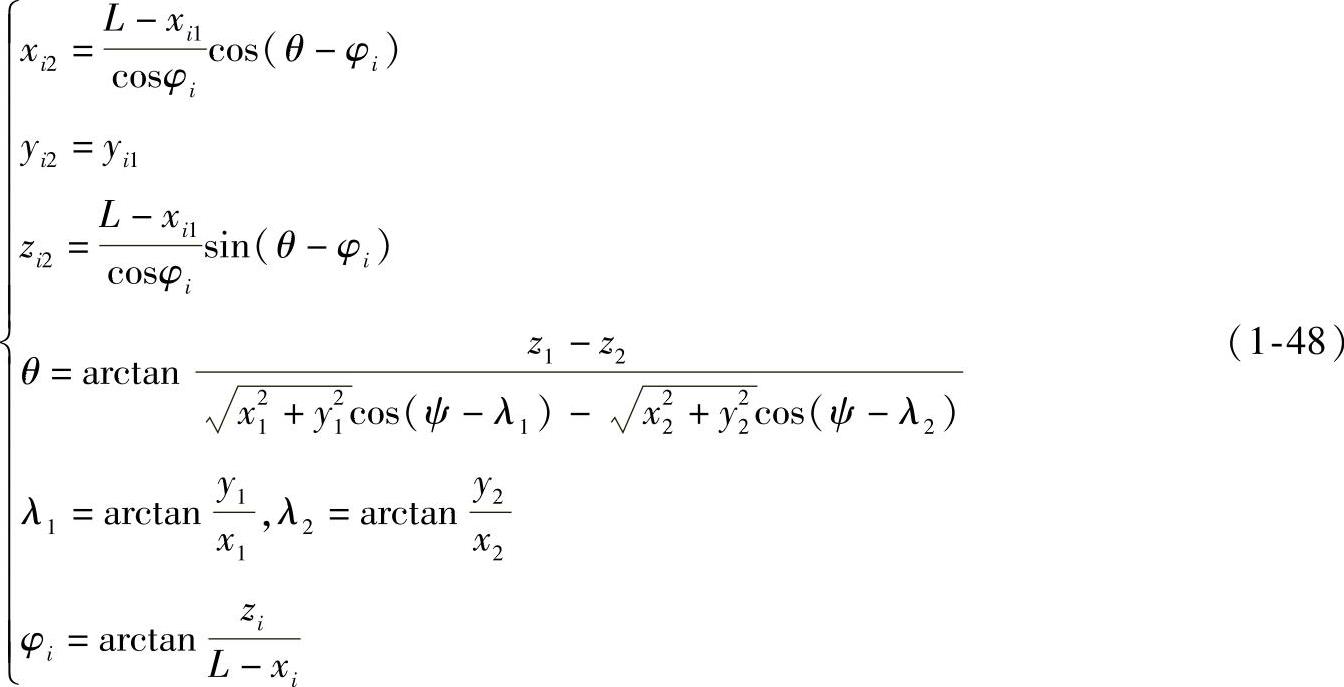
式(1-47)、式(1-48)即为一般位置平面变换成投影面的平行面的数学模型。
例1-9 已知A点的坐标为xa=50,ya=60,za=80;B点的坐标为xb=120,yb=20,zb=30,试求AB直线与H面的倾角α,如图1-48所示。
由图1-48可知,一次换面将直线变换为正平线,AB直线对H的倾角α为
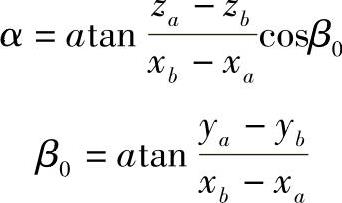
计算程序LP1-1.lsp(可通过扫描二维码观看)运行后由图1-49可知,直线AB对H面的倾角为31.8061°。

LP1-1.lsp程序
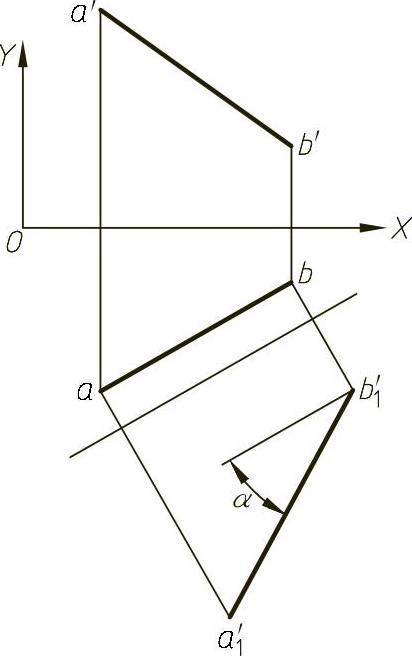
图1-48 求直线与H面的夹角

图1-49 直线AB对H面的倾角
3.求点到直线之间的距离
例1-10 已知点A的坐标为(xa,ya,za);BC直线的B点的坐标为(xb,yb,zb);C点的坐标为(xc,yc,zc),求点A到直线BC的距离。点与直线的投影如图1-50a所示。
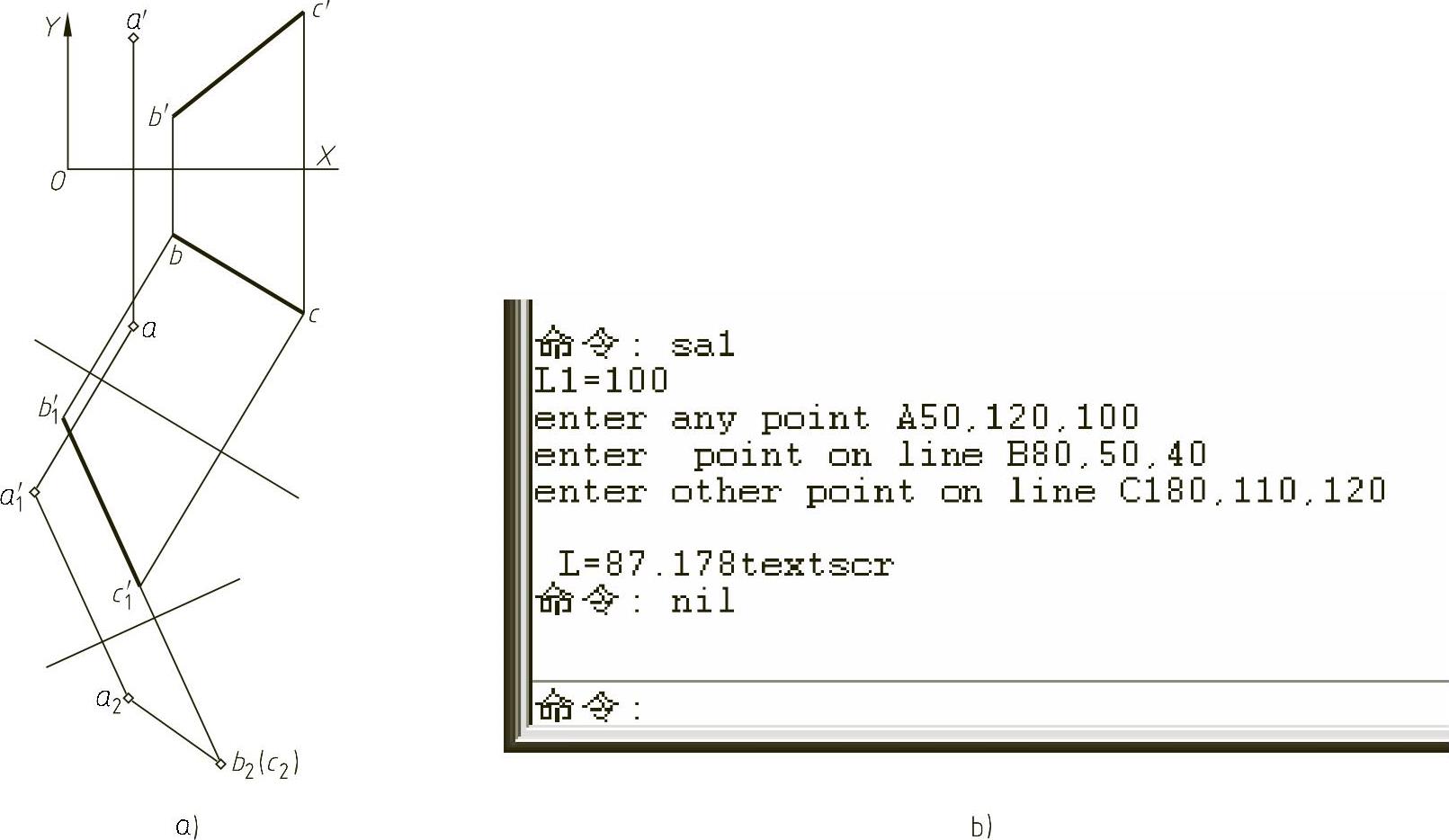
图1-50 求点到直线的距离
分析 作两次投影变换,将BC直线变换为铅垂线,A点随其一起变换,则在H2投影面上BC直线的投影为一个点,此投影点与A点的投影之间的距离即为点A到直线BC的距离。因此可用一般位置直线变换为投影面垂直线的数学模型求出(xa2,ya2)、(xb2,yb2),然后求得点A到直线的距离l=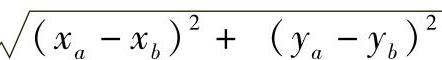 。
。
求点到直线距离的程序LP1-2.lsp可扫描二维码观看。程序运行后由图1-50b可知,A点到直线BC的距离为87.178mm。

LP1-2.lsp程序
4.求点到平面的距离
已知点A的坐标为(xa,ya,za),△BCD平面的B点的坐标为(xb,yb,zb);C点的坐标为(xc,yc,zc);D点的坐标为(xd,yd,zd),求A点到△BCD平面的距离。点A和△BCD平面的投影图如图1-51所示。
分析 作一次投影变换,将△BCD平面变换为正垂面,A点随其一起变换,则在V1投影面上△BCD平面投影积聚为一条直线,A点的投影与平面积聚性投影之间的距离即为点A到△BCD平面的距离。因此可用一般位置平面变换为投影面垂直面的数学模型求出(xa1,za1)、(xb1,zb1)、(xc1,zc1)、(xd1,zd1),在新投影面上点A到平面的距离变为A点的投影到平面的积聚性投影之间的距离,也即点a′1到直线b′1c′1d′1的距离。此距离可这样来求解,以a′1为圆心画一圆与平面的新投影(直线段)b1′c1′d1′相切,则切点与a′1之间的距离即为所求。设圆、平面新投影的方程为
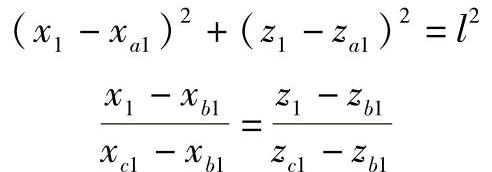
由此两方程可解出切点坐标为
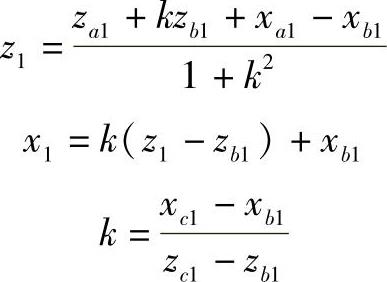
点到平面的距离即为
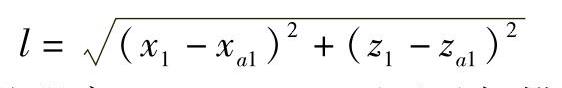 (https://www.xing528.com)
(https://www.xing528.com)
求点A到△BCD平面的距离的程序LP1-3.lsp(可通过扫描二维码观看)。程序运行后由图1-52可知,点到平面的距离为29.6618mm。
5.求直线与平面之间的夹角
已知A、B、C点的坐标为(xa,ya,za)、(xb,yb,zb)、(xc,yc,zc);E、F点的坐标为(xe,ye,ze)、(xf、yf,zf)。求直线EF与△ABC平面的夹角。直线EF和△ABC平面的投影如图1-53所示。

LP1-3.lsp程序
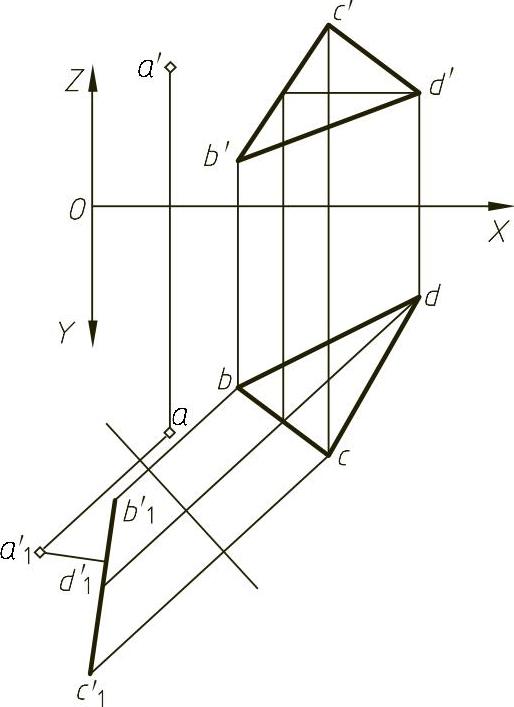
图1-51 求点到平面的距离

图1-52 点到平面的距离
分析 两次投影变换。先将△ABC平面变换为水平面,EF直线随之一起变换,再将平面和直线一起绕H2面的垂直线旋转,将EF直线转为V1面的平行线,由于△ABC已为H2面的平行面,因此绕H2面的垂直线旋转时其位置不变,则在V1投影面上△ABC平面与EF直线的投影之间的夹角即为所求。
求直线EF与平面△ABC的夹角程序LP1-4.lsp(可通过扫描二维码观看)。程序运行后由图1-54可知,EF直线与△ABC平面的夹角为60.8708°。

LP1-4.lsp程序
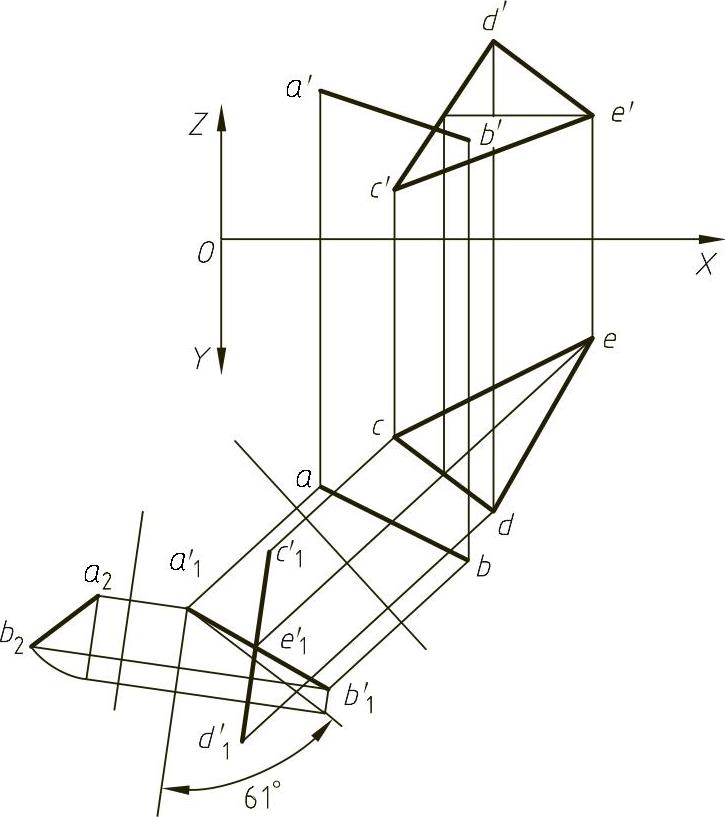
图1-53 求直线与平面之间的夹角

图1-54 直线与平面之间的夹角
6.机构定位实验
(1)机构定位数学模型的建立 图1-55所示为一空间曲柄滑块机构的示意图。工作时曲柄ρ=AB绕轴A—A在铅垂面Q内旋转,它牵动连杆L=BC,然后带动滑块C,使滑块C在平行于X轴的滑槽内左右滑动(B和C处均为球形铰接)。当曲柄从已知位置按箭头所示方向转动θ角后,则滑块C在滑槽内移动一段距离x,显然滑块C在滑槽内的移动距离x与曲柄旋转角度θ之间有函数关系x=f(θ)。为准确、直观地描述滑块C的运动状态,利用形数分析的方法建立滑块移动距离与曲柄旋转角之间的函数关系。
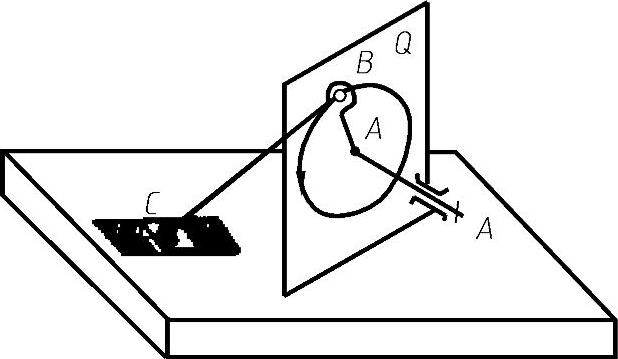
图1-55 空间曲柄滑块机构的示意图
(2)图解法 如图1-56a所示,将图解法分两步进行。
1)求B点转动θ角后的位置。先作一个新投影面V1平行于Q面,求出曲柄AB的新投影a1′b1′,以a′为圆心,a1′b1′为半径画圆弧,使B点转动θ角由b1′转到b′1θ的位置,然后再返回去求出B点转过θ角之后的水平投影bθ和正面投影bθ′。
2)求滑块C滑动后的位置。因为在机构运动过程中连杆BC的长度保持不变,且滑块C的运动轨迹为已知(一侧垂线),因此有以下作图步骤:
① 用直角三角形法求出连杆BC的实长。
② 根据连杆BC的实长求出C点运动后的连杆BC水平投影的长度。如图1-56b所示,单独作出一个直角三角形BCD,其中BD等于Bθ与Cθ两点高度差,则CD为经过滑动后连杆BθCθ的水平投影的长度。
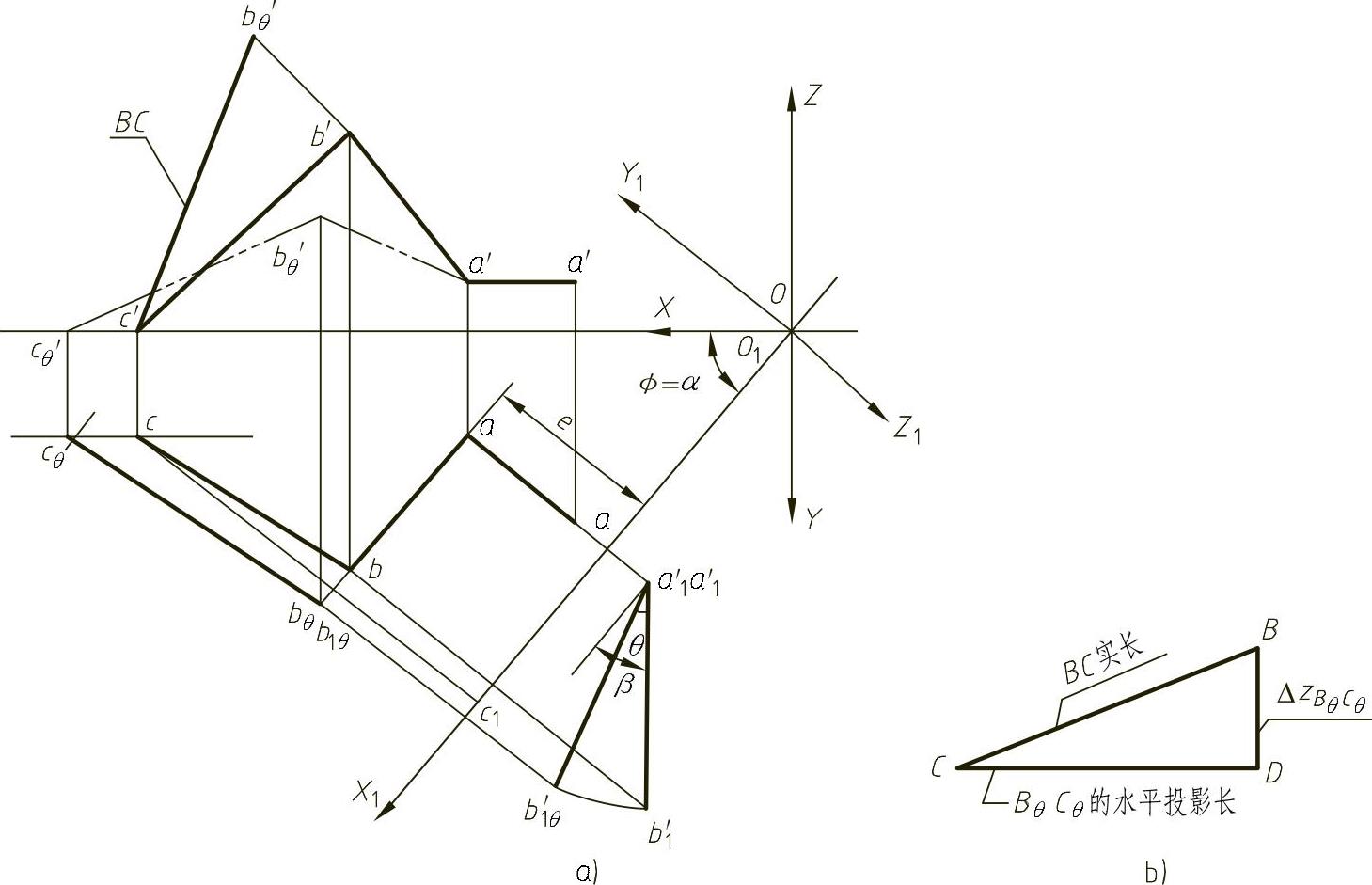
图1-56 机构运动图解
在图1-56a上以bθ为中心,CD为半径作圆弧,与过c点的水平线交于cθ并由此求出cθ′,则Cθ(cθ,cθ′)即为滑块的新位置,由此即得曲柄AB转动θ角后滑块C移动的距离x=c′cθ′。
3)建立滑块C移动距离x与曲柄AB转动角度θ之间的函数关系x=f(θ)。已知条件为α,AB=ρ,BC=L,e为任意常数,且A、B、C三个点的坐标分别为A(xa,ya,za),B(xb,yb,zb),C(xc,yc,zc)。由上述图解过程可知b1θb′1θ点在O1X1Y1Z1坐标系中的坐标为

式(1-49)中x′a1、y′a1,z′b1,za1即为A、B两点经一次换面后在新坐标系中的坐标。点bθ在OXY坐标平面中的坐标为
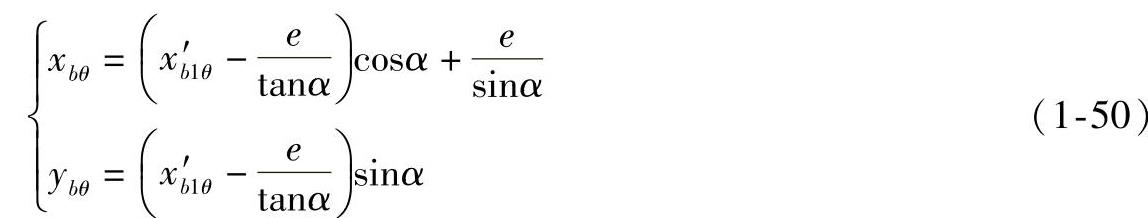
L的水平投影长为
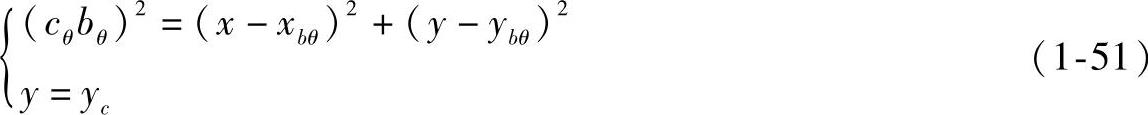
由式(1-51)得
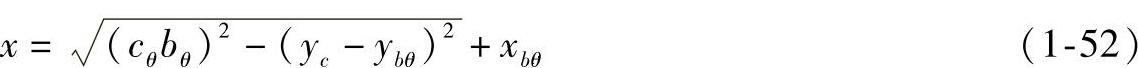
将式(1-51)代入式(1-52),联立式(1-49)、式(1-50),并令e=0,得
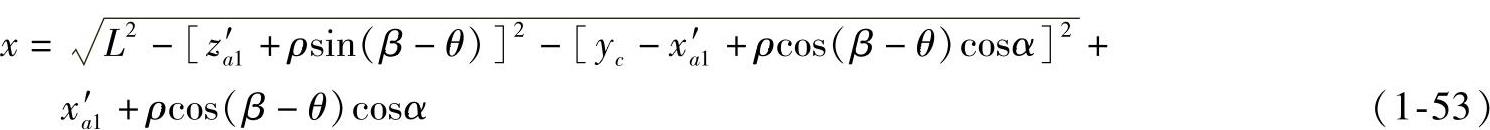
式(1-53)即为滑块C移动距离x与曲柄AB旋转角θ之间的函数关系。
将初始条件:曲柄长度,连杆长度,A、B、C三点坐标输入“参数输入”对话框,如图1-57所示,曲柄连杆机构运动“参数输入”对话框及计算滑块各位置坐标点的程序为LP1-5.dcl、LP1-5.lsp,可通过扫描相应二维码观看。滑块各位置坐标点的计算结果如图1-58所示。

LP1-5.dcl程序

LP1-5.lsp程序
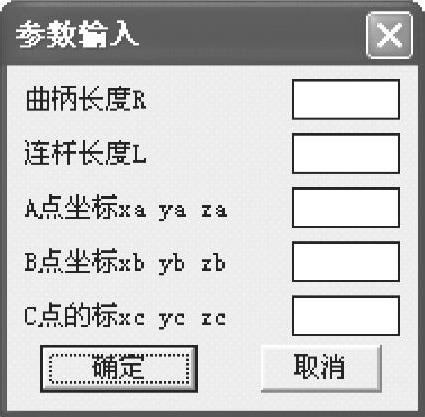
图1-57 “参数输入”对话框
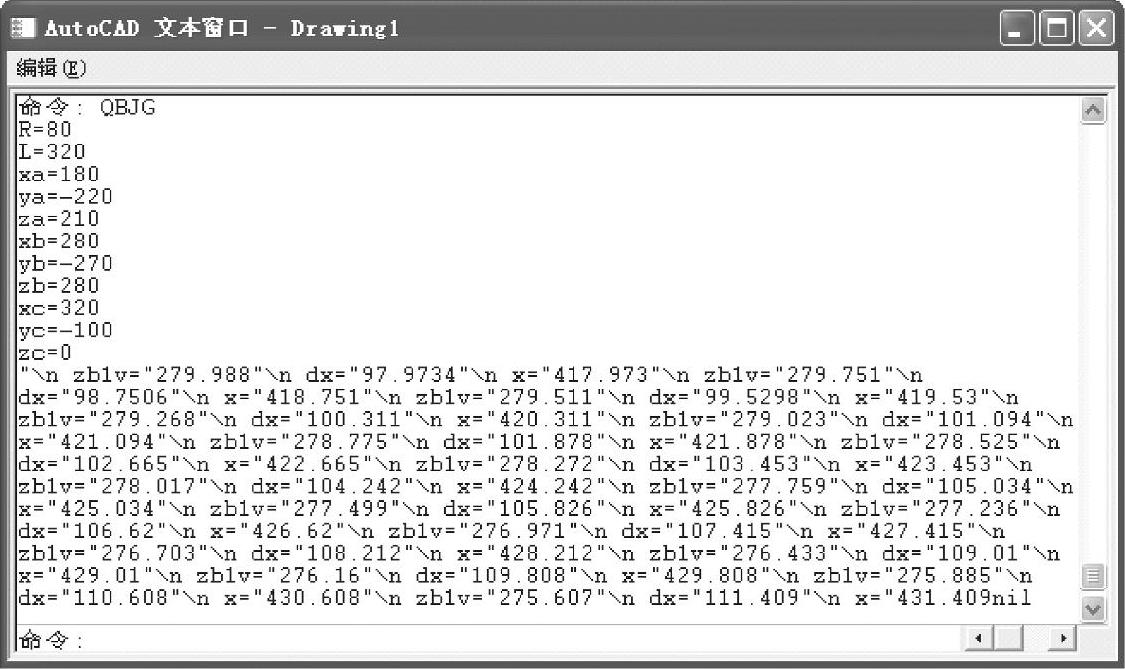
图1-58 运动计算结果
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




