空间几何元素的投影变换方法

由正投影原理可知，几何元素若与投影面处于一般位置时，其投影的度量性质是变化的，因此在利用画法几何方法图解几何度量和定位问题时，一般利用投影变换的方法使几何元素与投影面处于特殊位置，以便在新投影面上来度量几何元素的原形或使新投影更有利于解题。在此，所谓度量问题是指具有测量数值性质的问题，而所谓定位问题是指确定几何图形相互从属关系的问题。如图1-45所示，在点、线、平面范围内基本的度量、定位问题有：①两点之间的距离；②点至直线的距离；③点至平面的距离；④直线与平面的夹角；⑤平面与平面的夹角；⑥直线与平面的交点；⑦平面与平面的交线；⑧求平面的实形。

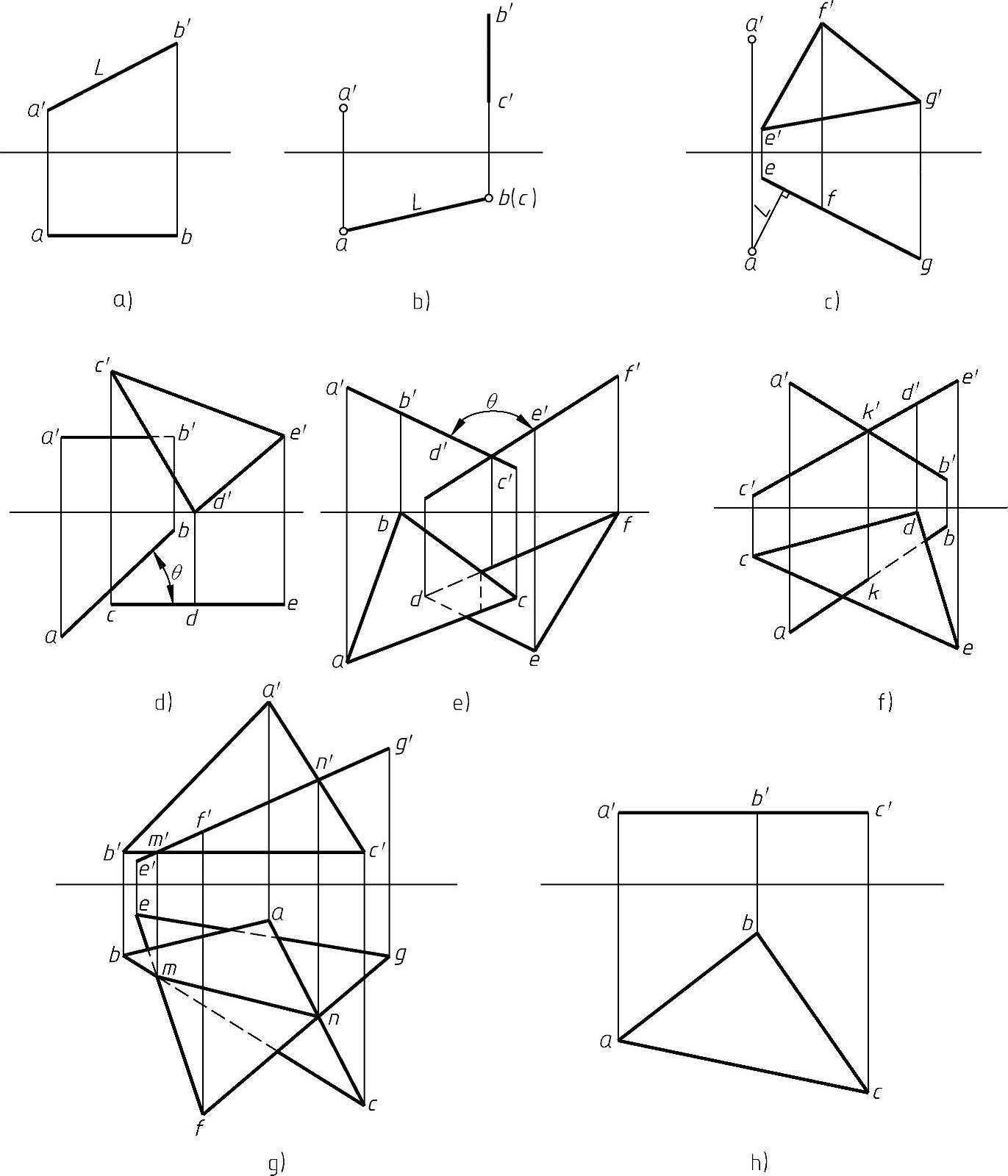
图1-45 几种常见的度量与定位问题

当构成这些度量、定位问题的几何图形与投影面处于一般位置时，则上述基本问题的解在投影面上的投影与解的原形之间存在着一定的关系。为了使这些问题的解能在投影面上直接得到反映，一般要通过如下方法作图：

1）对两点之间的距离，可将连接两点的直线变换为投影面平行线，则两点之间的距离L就在该投影面上反映实长，如图1-45a所示。

图1-45b～h所示几何元素已由一般位置变换到使问题易解的位置，变换过程从略。

2）对点至直线的距离，可将直线变换成某投影面的垂线，点也随之变换，则点到直线的距离L就在该投影面上得到反映，如图1-45b所示。

3）对点至平面的距离，可将平面变换成某投影面的垂直面，点也随之变换，则点到平面的距离L就可在该投影面上求得，如图1-45c所示。(www.xing528.com)

4）对一般位置直线与平面的夹角，可先作两次投影变换，将平面变换成正平面，直线随之变换，此时直线在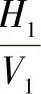投影体系中仍为一般位置直线。第三次投影变换，将直线变成水平线，则直线与平面的夹角θ可在水平投影面上得到，如图1-45d所示。

5）对两平面之间的夹角，可将两平面同时变换成投影面的垂直面，则两平面之间的夹角ϕ可在该投影面上得到，如图1-45e所示。

6）对直线与平面的交点，可将平面变换成投影面的垂直面，比如变换成正垂面，直线也随之变换，则在正投影面上得到交点的正面投影，由从属性可得交点的水平投影，如图1-45f所示。

7）对两平面的交线，可将其中一个变换成投影面的垂直面，比如变换成正垂面，另一平面也随之变换，则在正投影面上得到交线的正面投影，由从属性可得交线的水平投影，如图1-45g所示。

8）对平面的实形，可将平面变换成投影面的平行面，比如变换成水平面，则在水平投影面上可得到该平面的实形，如图1-45h所示。

上述各基本度量或定位问题需经过适当次数的投影变换。从理论上讲，只要在变换投影面的过程中，作图绝对准确，则其解也是精确的。但在实际作图时，要做到绝对准确是不可能的。每一步作图都带有误差，经过若干步作图后，其误差积累使其成为非精确解。为了既能利用投影变换的直观性，又能得到精确的结果，用形、数、计算机结合的方法使解题的过程体现直观性并能进行定量分析，从而由计算机精确求解，就必须在投影变换的基础上，寻求图形之间的量的联系，从而建立起解题的数学模型再根据数学模型设计计算机绘图程序，使问题在几何的、数学的、计算机图形相结合的方法中得到直观的精确解。