(1)直线与平面相交 图1-31a表示了用辅助面法求解的基本思路:如要求DE和△ABC的交点,可先包含已知直线DE作辅助面P(为了求解方便,通常选用特殊位置面作辅助面),然后求出P面与已知面ABC的交线MN,则同在P面上的直线DE和交线MN必相交,其交点K即为所求DE和△ABC的交点。
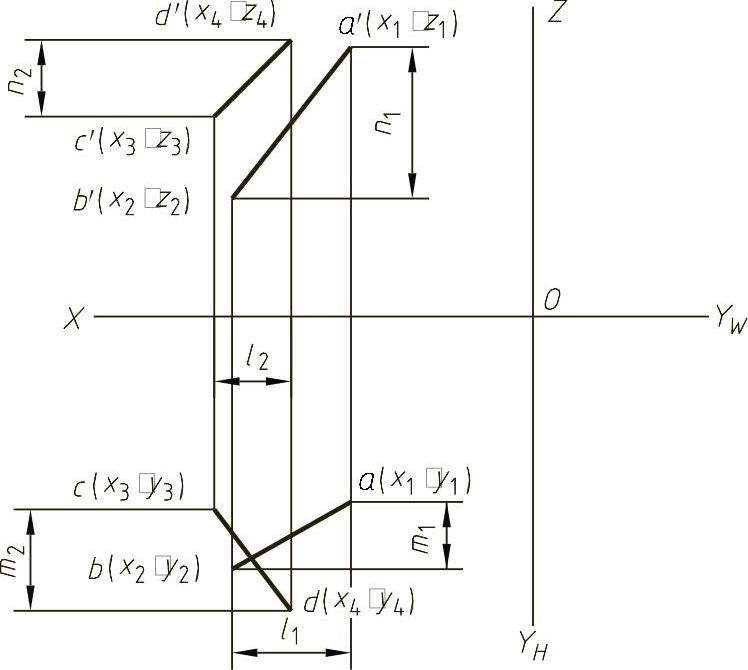
图1-30 交叉两直线的投影
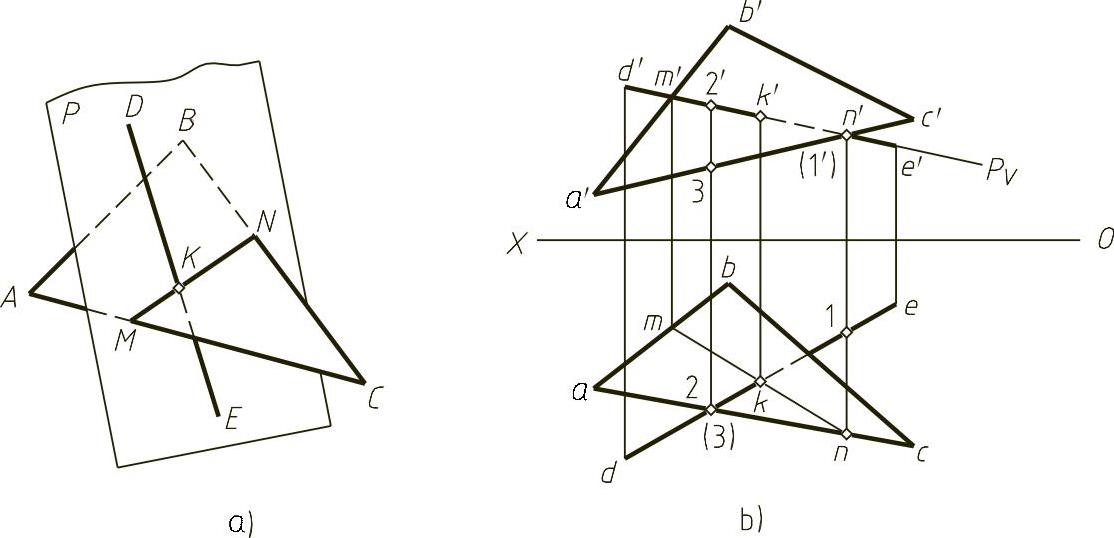
图1-31 求一般位置直线与一般位置平面相交的交点
下面结合图1-31b,介绍求交点的具体步骤:
1)包括已知线作辅助面。在图1-31b中,过DE作正垂面P,其正面投影PV积聚为一条线与d′e′重合。
2)求已知面与辅助面的交线为m′n′和mn。
3)求出该交线与已知线的交点,即为所求线、面的交点。图1-31b中de与mn的交点k,为所求线、面交点的水平投影。其正面投影k′可按投影规律在d′e′上作出。
由于直线和平面在投影中有部分重合,所以在求出交点后,还需判别其可见性。图1-31b中利用重影点Ⅱ、Ⅲ,可判定水平投影中dk段为可见;利用重影点Ⅰ、N可判别正面投影中k′n′段为不可见。
同样可以选择过直线MN的铅垂面为辅助面,求解结果完全相同。必须注意,正面投影和水平投影的可见性问题,必须分别用重影点判别之。
设直线方程为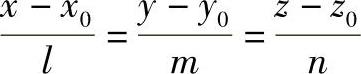 ,平面方程为Ax+By+Cz+D=0,交点坐标可由公式
,平面方程为Ax+By+Cz+D=0,交点坐标可由公式
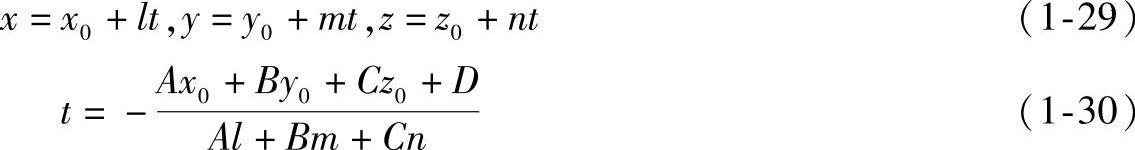
求解。
当已知平面上三点M1(x1,y1,z1),M2(x2,y2,z2),M3(x3,y3,z3)时,平面的法向矢量为
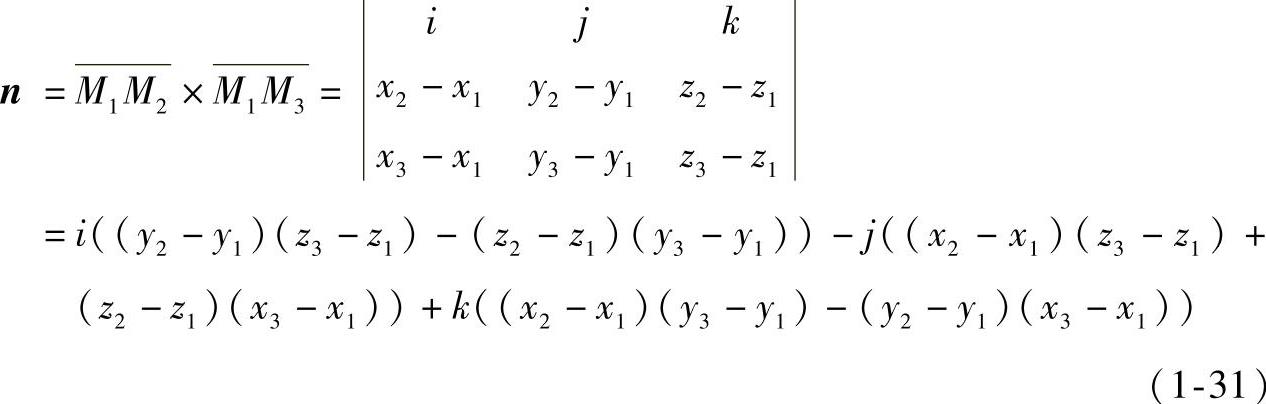
由此可得平面方程的系数
A=(y2-y1)(z3-z1)-(z2-z1)(y3-y1) (1-32)
B=-(x2-x1)(z3-z1)+(z2-z1)(x3-x1) (1-33)
C=(x2-x1)(y3-y1)-(y2-y1)(x3-x1) (1-34)
由图1-32可知,当直线与平面以投影图形式给出时,可以从图上量取直线的方向数l、m、n和直线上一点的坐标(x0,y0,z0),并量取平面上三点坐标M1(x1,y1,z1),M2(x2,y2,z2),M3(x3,y3,z3),代入式(1-32)、式(1-33)、式(1-34)计算出系数A、B、C与l、m、n、(x0,y0,z0),一起代入式(1-29)、式(1-30),即可算出交点坐标。
如从图1-32中量取DE直线的方向数为:l=24.8504,m=14.2379,n=5.4499;平面三点坐标为:M1(40.8531,16.6657,4.1827),M2(28.4383,3.9921,19.7149),M3(11.3850,18.9793,11.1313),直线上D点的坐标为D(38.1132,20.1999,14.1288),经式(1-29)、式(1-30)计算交点K的坐标为K(25.5052,13.0236,11.3413),与图解得到的K点坐标一致,同时反映了直线与平面相交的可见性问题。
(2)直线与平面平行 由初等几何的定理可知,直线和平面平行的充分必要条件是该直线平行于平面上的某一直线。体现在投影图上,直线与平面平行,则直线与平面上某一直线的各个同面投影均相互平行,否则该直线与平面在空间不平行。

图1-32 直线与平面交点的形数结合求解
图1-33表明了直线KL平行于属于△ABC上的直线ⅠⅡ,则KL与△ABC在空间必然平行(见图1-33a)。反映在投影图中1′2′在△a′b′c′上,12在△abc上,而1′2′∥k′l′,12∥kl(见图1-33b)。(https://www.xing528.com)
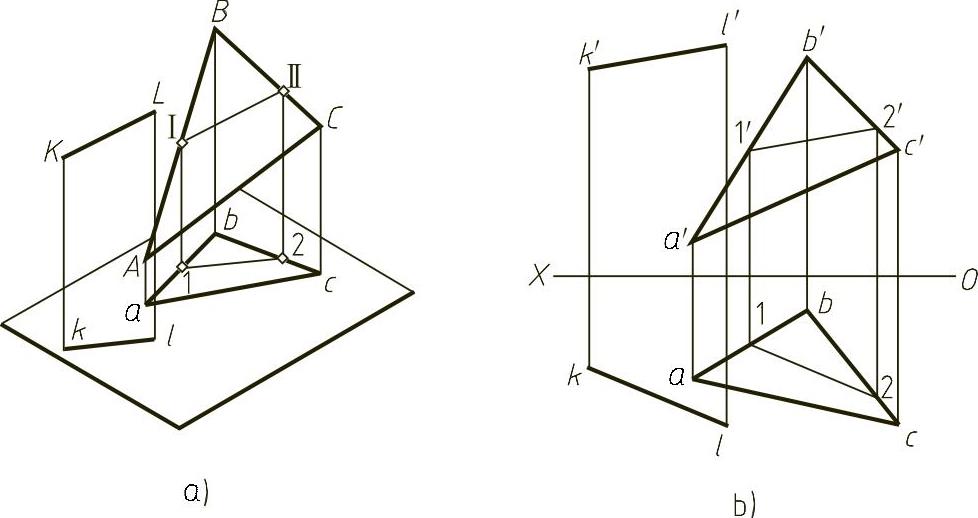
图1-33 直线与平面平行
运用上述定理可以解决直线与平面平行的作图和判别问题。
设直线方程为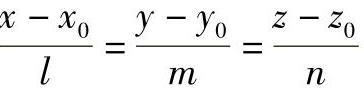 ,平面方程为Ax+By+Cz+D=0,则直线与平面平行的充要条件为
,平面方程为Ax+By+Cz+D=0,则直线与平面平行的充要条件为

证明:在平面上取两点p3(x3,y3,z3)和p4(x4,y4,z4),代入平面方程中并相减得
A(x4-x3)+B(y4-y3)+C(z4-z3)=0 (1-36)
将式(1-36)两边除以(x4-x3)得

若p3p4直线与给定直线平行,则有

式(1-38)、式(1-39)分别说明两直线在H、V面上的投影的斜率相等,将式(1-38)、式(1-39)左边项代入式(1-37)并乘以l得Al+Bm+Cn=0,证明完毕。
(3)直线与平面的夹角
定理:过直线和平面的交点B在该平面上引诸直线,其中和已知直线夹角最小的那一条直线,是已知直线在该平面上的正投影,如图1-34所示。
定义:直线和它在平面上的投影所成的锐角,称为该直线对该平面的夹角。图1-34b所示,求直线DE对平面△ABC的倾角θ的示意图,图1-35所示为求解过程。其解题步骤如下:
1)任取属于直线DE的一点D,由D作△ABC的法线DF(为此,在平面内作正平线、水平线)。
2)求出直线DE和法线DF的夹角ϕ(用直角三角形法求出DE、DF、EF实长构造△DEF实形)。
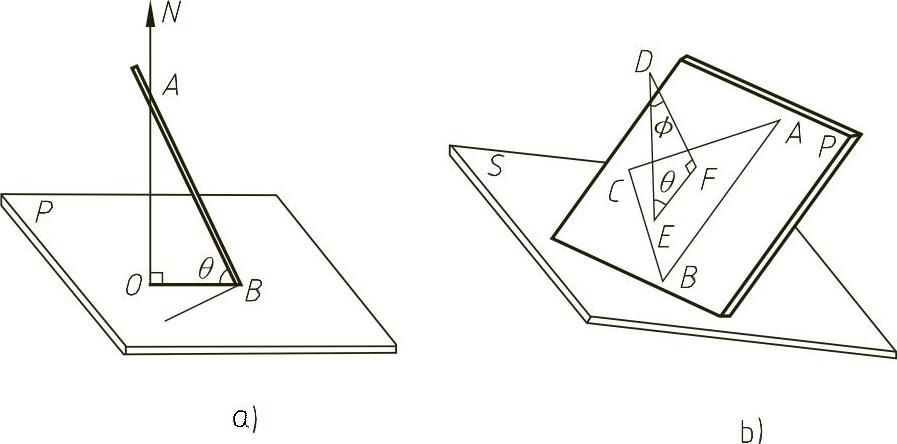
图1-34 直线与平面的夹角
3)ϕ角的余弦便是直线DE对平面△ABC的倾角θ。

图1-35 直线与平面夹角的示意图与图解过程
如果给出直线AB的方程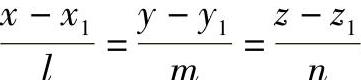 和平面的方程Ax+By+Cz+D=0,因ϕ角的余角是直线AB对平面P的倾角θ,所以直线AB对平面P的倾角计算公式为
和平面的方程Ax+By+Cz+D=0,因ϕ角的余角是直线AB对平面P的倾角θ,所以直线AB对平面P的倾角计算公式为
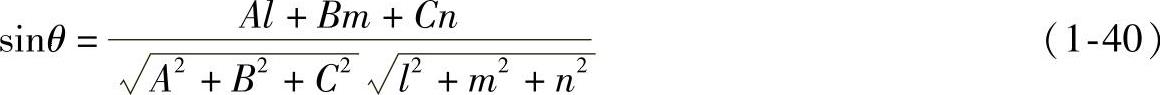
当已知直线和平面的投影时,如图1-36所示,可在图上量取平面上三个点的坐标,由三点求出平面方程的系数A、B、C,再在图上量取直线的方向数l、m、n,代入式(1-40)即可得到直线与平面的夹角θ。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




