(1)平行两直线 在投影空间中两直线平行,则它们的同面投影均相互平行,如图1-24所示。空间AB和CD两直线平行,由于投影方向一致,故ABba和CDdc为两个平行平面,则它们与H面的交线ab和cd也相互平行,同理可知a′b′∥c′d′,a″b″∥c″d″。

图1-24 平行两直线的投影特性
已知两直线l1: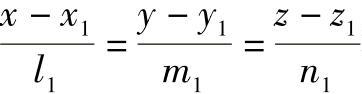 和l2:
和l2: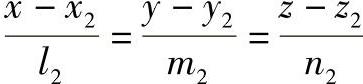 ,则两直线平行的条件为
,则两直线平行的条件为
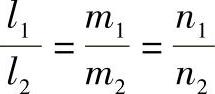
当两平行直线各端点位置确定后,方程中各参数l1、m1、n1,l2、m2、n2在投影图中都有对应的大小,如图1-25所示。由此,可在平行两直线的投影图上量取l1、m1、n1,l2、m2、n2,并各取一个点的坐标,即可将投影图转换成平行两直线的方程式。
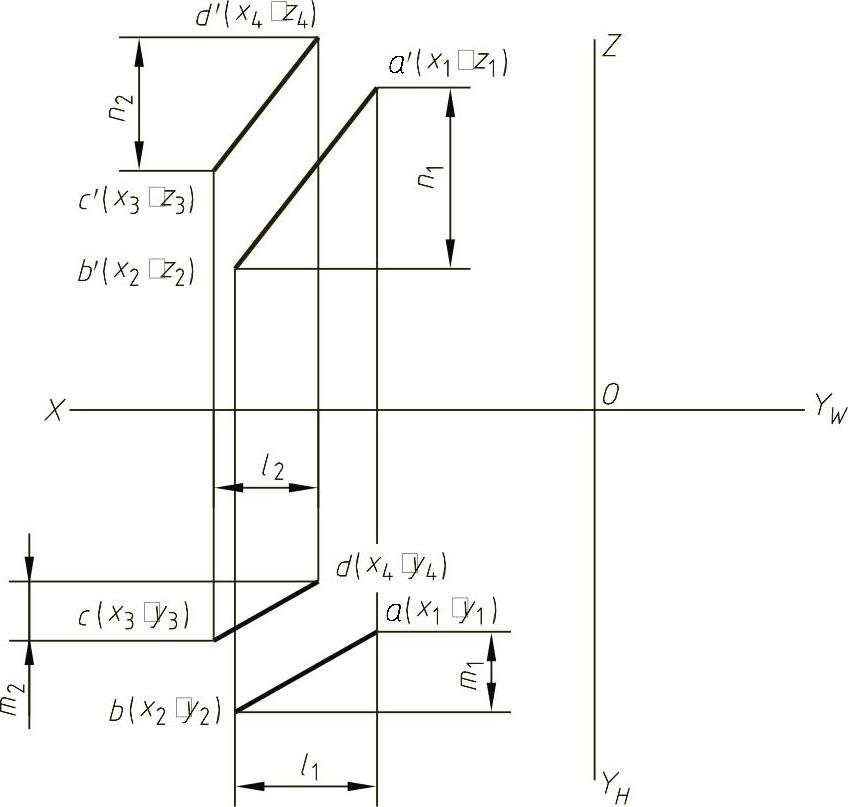
图1-25 平行两直线方程中各参数的几何含义
(2)相交两直线 两直线在空间相交,其同面投影必相交,且交点的连线垂直于相应的投影轴。如图1-26所示,空间两直线AB、CD相交于K点,由于交点是两直线共有点,根据直线上点的从属性可知,K点的水平投影k必在ab和cd的交点上,同样k′必在a′b′和c′d′的交点上,k″必在a″b″和c″d″的交点上。又由于k、k′、k″均为空间点K的投影,所以它们必满足点的投影规律,即k′k⊥OX,k′k″⊥OZ,kk″⊥OY。当已知两直线方程时,为了求得两直线交点的坐标,先将两直线化成参数式,即
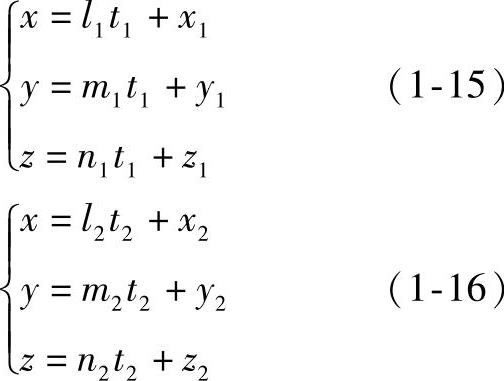
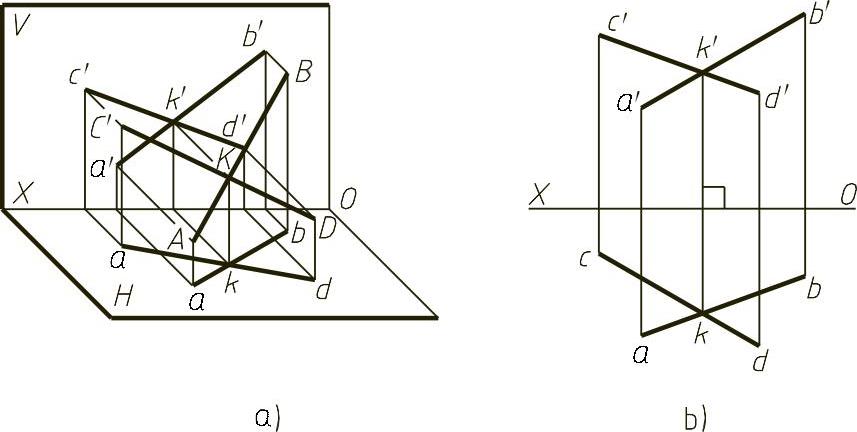
图1-26 相交两直线
因交点是两直线公共点,故有

利用式(1-17)的前两式即可求出t1、t2,得
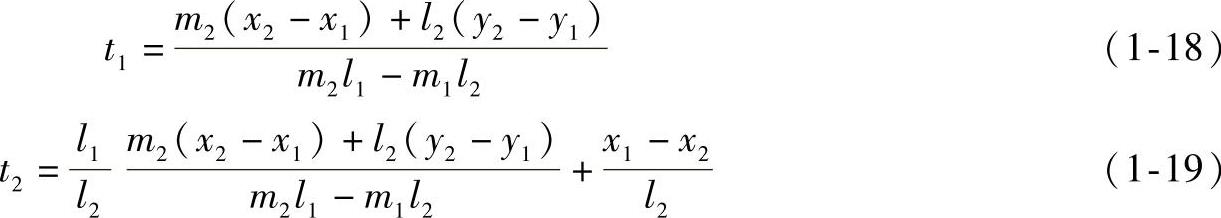
将所求的t1、t2代入直线参数方程式(1-15)或式(1-16)即可求得交点坐标。
反过来,当相交两直线各端点位置确定后,从投影图(图1-27)上量取l1、m1、n1,l2、m2、n2和交点K的坐标,即可得到两相交直线的参数方程,即

(3)交叉两直线 空间两直线交叉,它们的投影既不符合两直线平行的投影特性,也不符合两直线相交的投影特性。如图1-28b所示,AB和CD两直线的V面和H面投影虽然相交,但交点连线不垂直于X轴,故其水平投影ab和cd的交点1、2和正面投影a′b′和c′d′的交点3′、4′点,实际上是重影点。根据重影点前遮后、上遮下、左遮右的原则可以判定两直线的空间位置。从图中可见,对应重影点1、2是正面投影c′d′上的1′点和a′b′上的2′点,其中1′点高于2′点(z坐标大),故对水平投影而言,1在2之上为可见,2在1之下被遮住为不可见,加括号表示;同理,正面投影的重影点上,根据3、4点的y坐标大小,可知3点在前为可见,4点在后为不可见,空间情况如图1-28a所示。
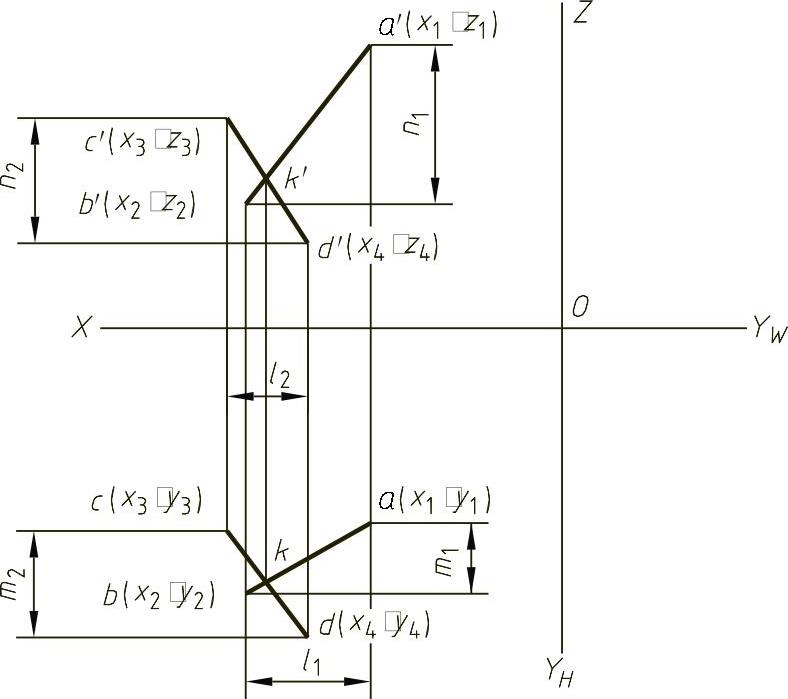
图1-27 相交两直线的投影
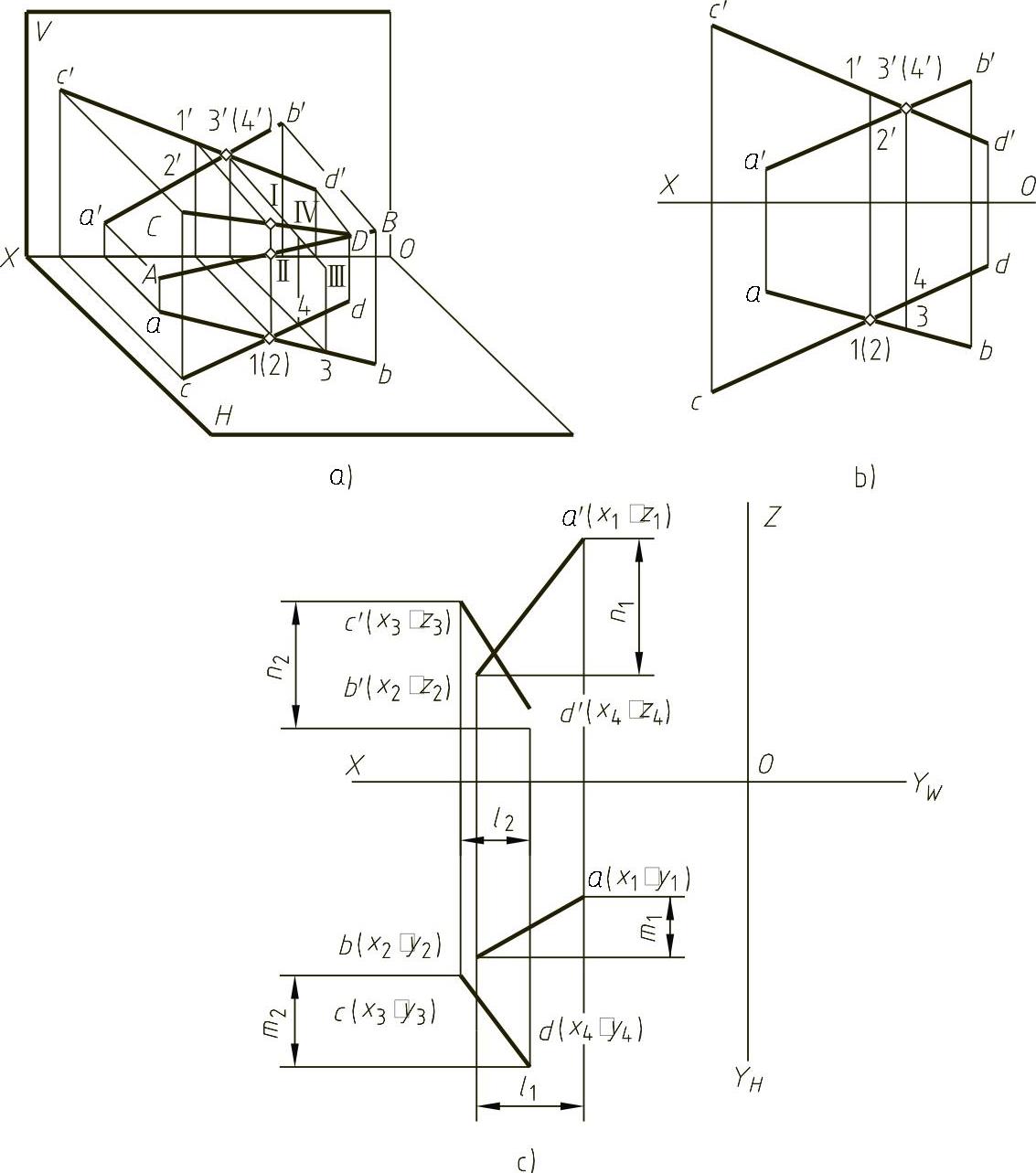
图1-28 交叉两直线的投影
设两直线方程分别为:(https://www.xing528.com)
直线AB
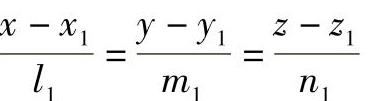
直线CD

交叉两直线的判别条件是
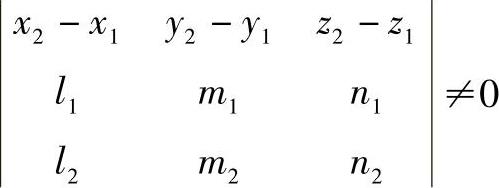
由此可知,当交叉两直线各端点位置确定后,从投影图1-28c上量取l1、m1、n1,l2、m2、n2,并分别在两直线上取点P1和P2的坐标,代入判别条件计算,如果行列式不等于0,则说明空间两直线处于交叉位置。
(4)两直线的夹角 若两直线为无向直线,则它们之间的锐角定义为两直线的夹角,用θ表示,如图1-29a所示。设两直线方程分别为:
直线AB
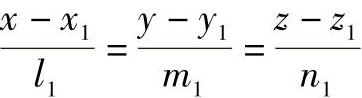
直线CD
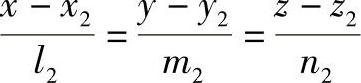
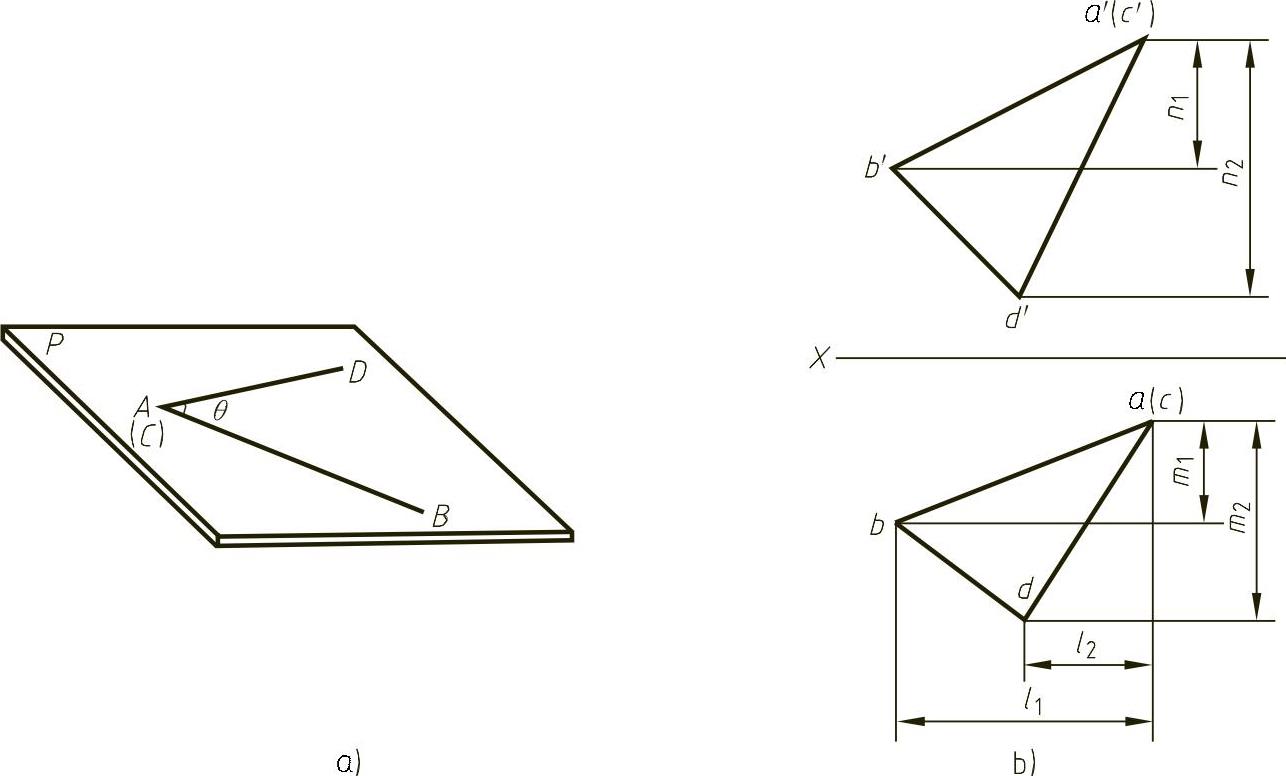
图1-29 两直线的夹角及其投影
如果两直线AB和CD相交于A(C)点,为求∠BAD,也即求AB、AD和BD各边的实长构成的△BAD,由图1-29b可知,各条边的实际长度为
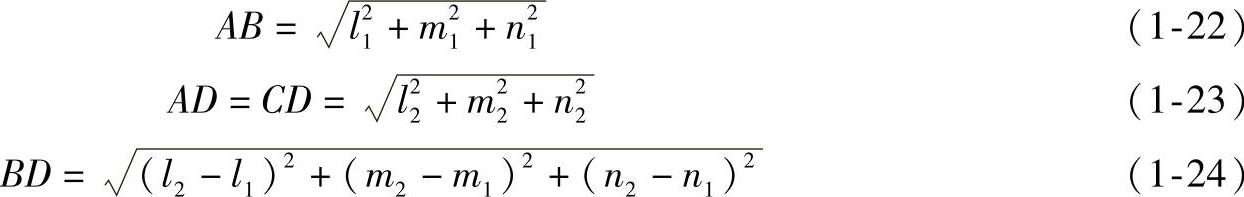
根据余弦定理知

若θ=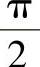 ,则两直线互相垂直,这时cosθ=0,即
,则两直线互相垂直,这时cosθ=0,即
cosθ=l1l2+m1m2+n1n2=0 (1-26)
根据上述内容可知,当交叉两直线的投影位置确定后,如图1-30所示,可在图上量取l1、m1、n1,l2、m2、n2各参数的长度,代入式(1-26)即可计算出两直线的夹角。
(5)交叉两直线的距离 当交叉两直线的方程确定后,在空间解析几何中该交叉两直线的距离由公式
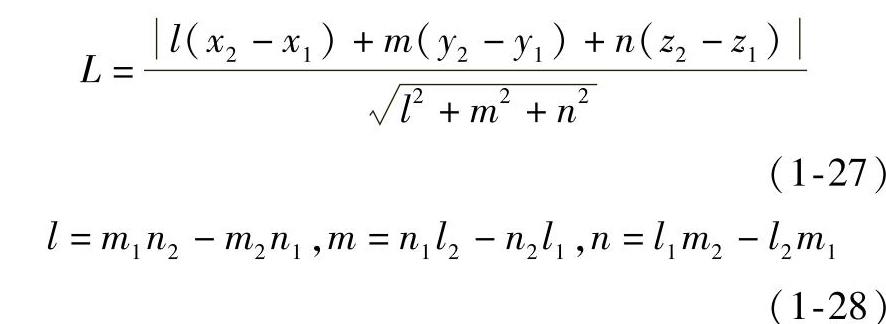
求解,根据图1-30可知,当交叉两直线用投影表示时,可在投影图上量取公式中的各参数和在两条线上各取一点的坐标,即可用式(1-27)、式(1-28)计算出交叉两直线的距离L。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




