平面点与直线计算-计算机实验工程图形学.下册

在图示工程上各类物体时，经常涉及在平面上取直线和点的问题。例如，图1-16所示为一经切割的三棱锥，其中K点是平面SAB上的点，LK和MK则为该平面上的直线。下面分别加以讨论。

1.直线在平面上的条件及其作图

由初等几何可知，直线在平面上必须具备下列条件之一：①过该平面上两个点；②过该平面上一个点，且平行于该平面上任一条直线。

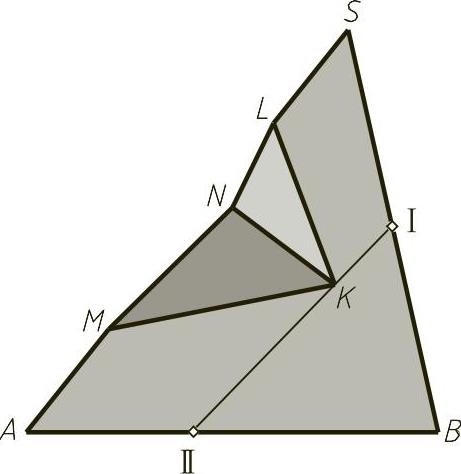
图1-16 平面上的直线和点

因此，凡在平面上作直线，只要通过其上两个已知点或过一已知点且平行于其上一已知直线。

例1-5 试在△ABC上作一条直线。

解 由图1-17a所示的立体图可知，过△ABC平面上AC线上的L点和AB线上的K点的连线LK，必在该平面上。在投影图上，该直线的投影即为该两点同面投影的连线lk和l′k′，如图1-17b所示。

同样，过△ABC上的M点，且平行于面上AB线的直线MN也必在该平面上。投影图上即为过m和m′，且分别平行于ab和a′b′的直线mn和m′n′，如图1-17c所示。

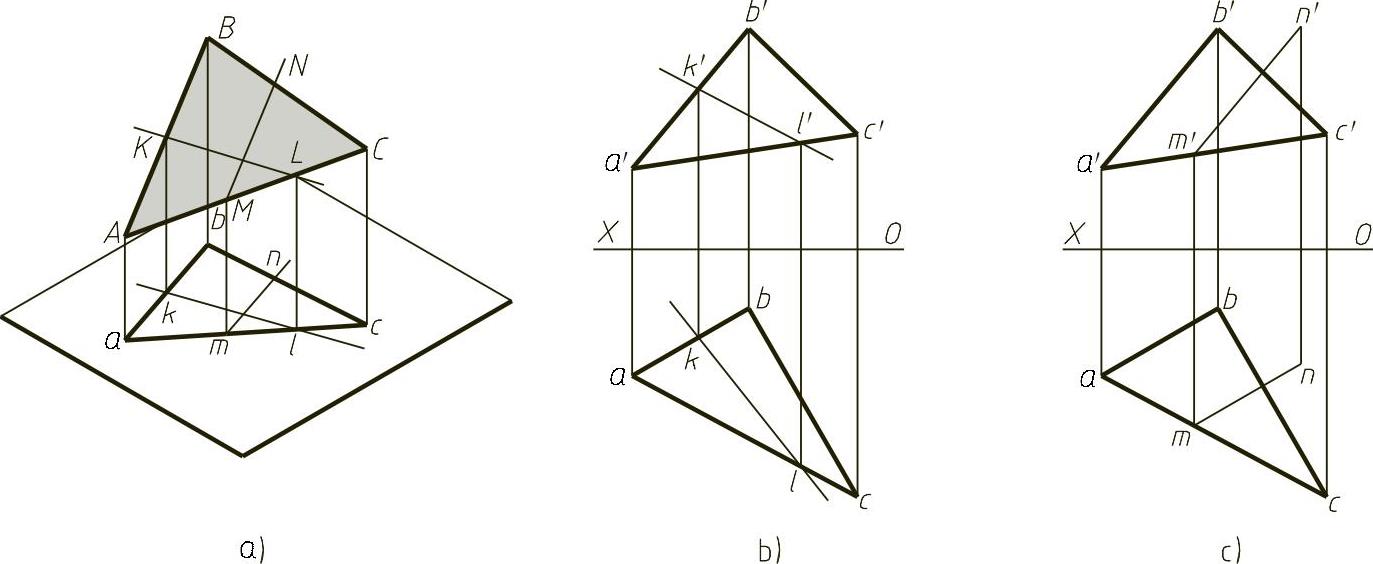
图1-17 平面上作直线

2.平面上的投影面平行线的作图

根据直线在平面上的条件，在平面上可以作出无数条直线，其中有一种既具有平面上直线的投影特性，又具有投影面平行线投影特性的直线，称为平面上的投影面平行线。如图1-18所示，直线AE在□ABCD上，且平行于水平面，所以是平面上的水平线，在投影面上a′e′∥X轴；直线AF为平面上的正平线，在投影面上af∥X轴。这种直线由于作图方便，常用作平面上的辅助线。

例1-6 如图1-19所示，已知△ABC的正面投影△a′b′c′和水平投影△abc，试在该平面上作一距离H面20mm的水平线。

解 由水平线的投影特性可知其正面投影为平行于X轴的直线，故作图必须从正面投影开始，由X轴往上度量20mm作一条通过△a′b′c′上d′、e′两点且平行于X轴的直线，即为要作的水平线正面投影；再根据投影关系分别求出△abc上的d、e两点，将其相连，就得到了要作的水平线的水平投影。

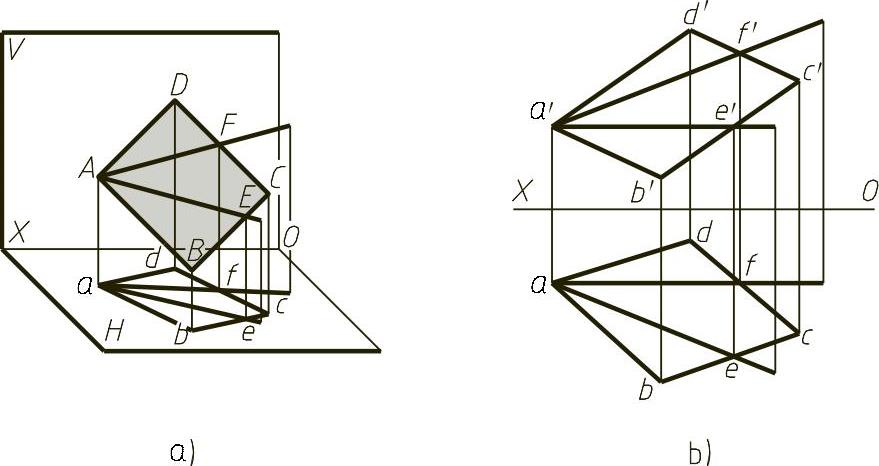
图1-18 平面上的投影面平行线

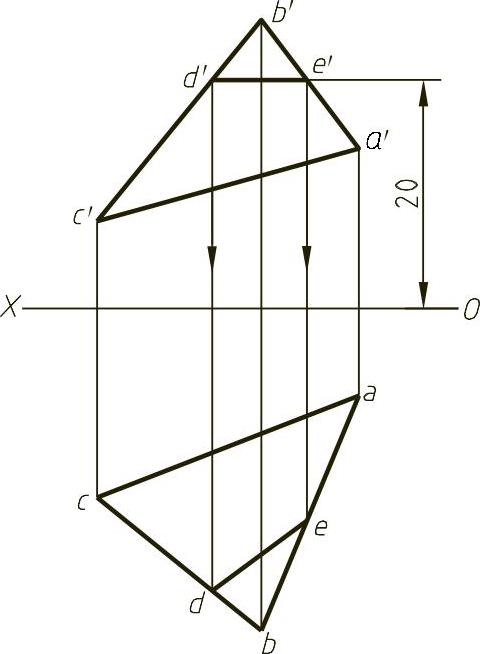
图1-19 按已知条件作投影面平行线

3.平面上最大斜度线的作图

平面内与某一投影面成最大倾角的直线，称为平面上对该投影面的最大斜度线。在平面内有无数条最大斜度线，它们是一组互相平行的直线。最大斜度线具有如下投影特性：(www.xing528.com)

1）对投影面倾角最大的直线。

2）最大斜度线垂直于平面内的投影面平行线。

3）平面对投影面的夹角等于平面内的最大斜度线对投影面的倾角。

如图1-20所示，直线EF是属于平面P的水平线，垂直于EF且属于平面P的直线AB是对H面的最大斜度线。在图1-20上，过点A作最大斜度线以外的也属于平面的任意直线AC。它对H面的角度为θ，因为AB⊥EF，且CB//EF，故AB⊥CB。根据直角投影定理，aB⊥CB，则aC＞aB，两个直角三角形ACa和ABa有相等的直角边Aa，而另一对直角边aC＞aB，故相应的锐角θ＜α。即最大斜度线对投影面的倾角最大。在图1-20中，平面P与H面构成两面角，此两面角α即为最大斜度线AB对H面的倾角。如图1-21所示，给定一平面△ABC。为求该平面的对H面的倾角，先作一属于该平面的对H面的最大斜度线CM。再用直角三角形法求出CM对H面的角度α即是。欲求该平面对V面的倾角β，则要用对V面的最大斜度线，如图1-22所示，作出的CM对V面的角度β即是。

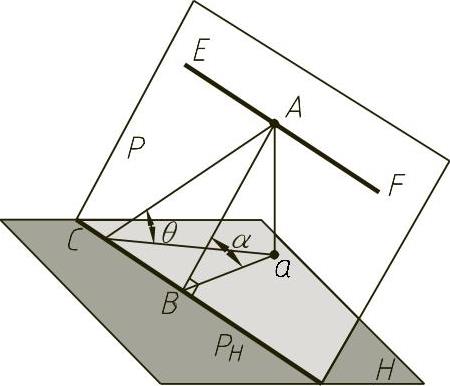
图1-20 最大斜度线

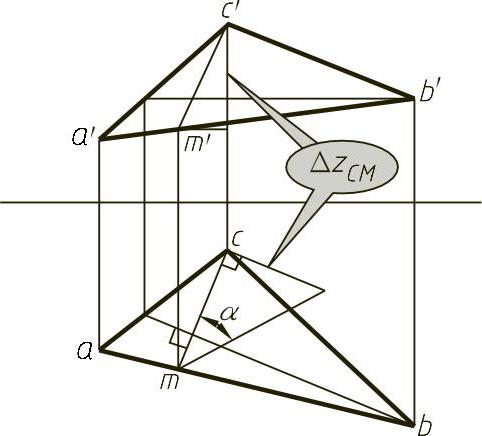
图1-21 平面对H面的夹角

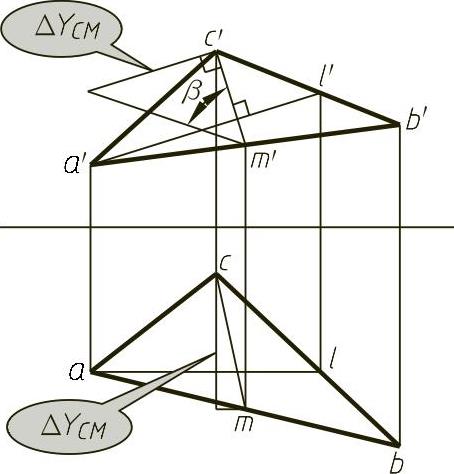
图1-22 平面对V面的夹角

4.满足平面方程的点和直线

设平面方程为Ax+By+Cz+D=0；直线方程为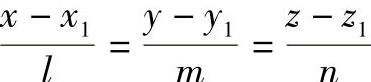，若该直线在平面上，则必须满足条件

Al+Bm+Cn=0 （1-13）

若平面上有任意点K（x₁，y₁，z₁），则有

Ax₁+By₁+Cz₁+D=0 （1-14）

例1-7 判断直线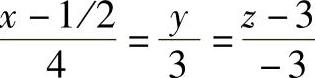是否在平面Q（方程为3y+2z-6=0）上，并画出投影图加以验证。

解：1）由式（1-13）可知，0×4+3×3+2×（-3）≠0，故该直线不在平面Q上。

2）由平面方程可知，A=0，则Q平面为侧垂面。令y=0时，z=3，其正面迹线为Q_V（Q_V⊥OZ）；令z=0时，y=2，其水平迹线为Q_H（Q_H⊥OY）。在直线上任取两点，取t=0，则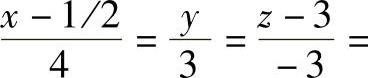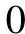，得点N（1/2，0，3）；取t=1，得点M（9/2，3，0）。由坐标可知N（n′，n）为该直线的正面迹点，其投影如图1-23所示。N点在Q_V上，M点不在Q_H上，故直线不在平面上。

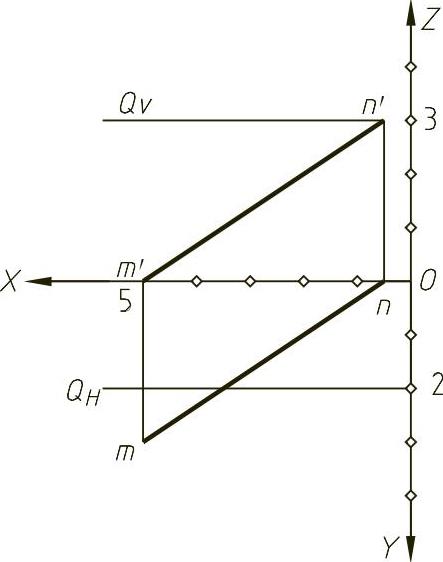
图1-23 判断直线是否在平面上