空间物体上的平面在三投影面体系中的投影,是由构成该平面的点、线等几何元素的同面投影所确定的,因此,在投影图中可以用下面任一组几何元素的投影表示平面,如图1-12所示。
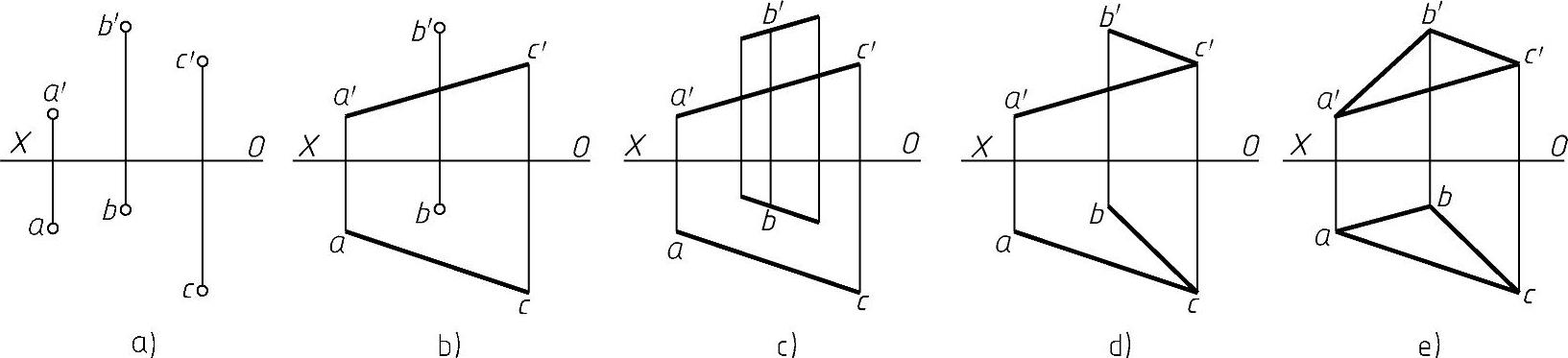
图1-12 表示平面的各种几何元素
a)不在同一直线上的三点 b)一直线和线外一点 c)两平行直线 d)两相交直线 e)任意的平面图形(如三角形、圆等)
从图1-12中可见,各种表示法可以相互转化,而其中不在同一直线上的三点是决定平面位置的基本几何元素。
给出不共线的三点P1(x1,y1,z1),P2(x2,y2,z2),P3(x3,y3,z3),就可以唯一地确定一个平面,设P(x,y,z)为平面上任一点,它满足共面的条件为
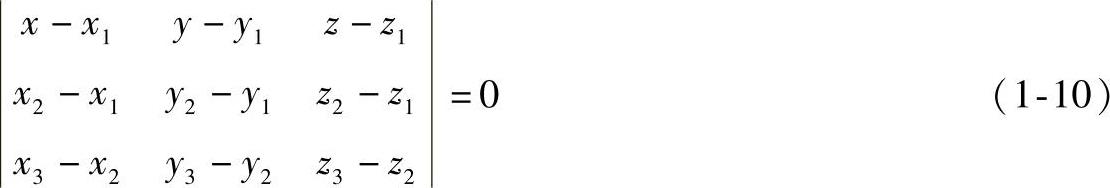
由此共面条件可得平面P的一般方程为
Ax+By+Cz+D=0(A2+B2+C2≠0) (1-11)
根据式(1-11)绘制平面的方法是求出平面与各坐标轴X、Y、Z的交点,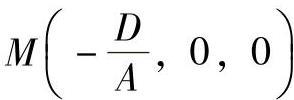 ,
,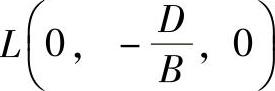 ,
,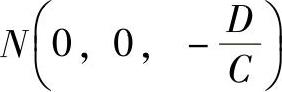 ,连接NM得到平面与V投影面的交线,成为平面迹线PV,连接ML得到平面与H投影面的交线,成为平面迹线PH,连接LN得到平面与W投影面的交线,成为平面迹线PW。如图1-13所示,PV、PH、PW三条迹线构成的平面称为迹线平面。过M、L、N三点的平面方程的坐标形式是
,连接NM得到平面与V投影面的交线,成为平面迹线PV,连接ML得到平面与H投影面的交线,成为平面迹线PH,连接LN得到平面与W投影面的交线,成为平面迹线PW。如图1-13所示,PV、PH、PW三条迹线构成的平面称为迹线平面。过M、L、N三点的平面方程的坐标形式是

因为a、b、c为平面在坐标轴上的截距,所以方程式(1-12)称为平面的截距方程。(https://www.xing528.com)
例1-3 将平面6x+9y+5z-54=0用迹线平面的投影图表示。
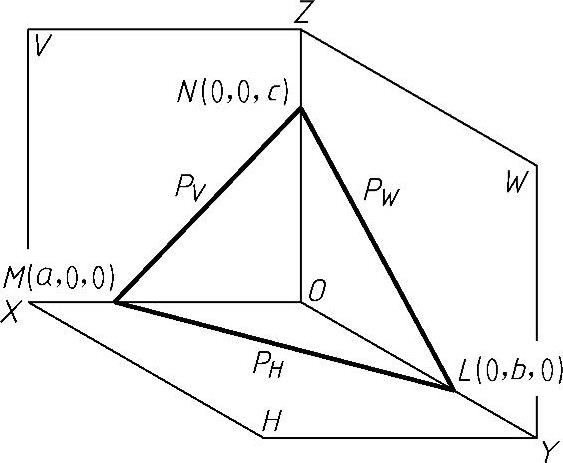
图1-13 迹线平面
解 由式(1-11)、式(1-12)可知,该平面与三个坐标轴的截距为:a=9,b=6,c=10.8,据此可定出平面与三个坐标轴的交点M、L、N,连接M、N,M、L,L、N,即可得PV、PH、PW三条迹线,如图1-14所示。
例1-4 根据图1-15中A、B、C三点的投影,写出此三点所代表的平面的截距式方程。
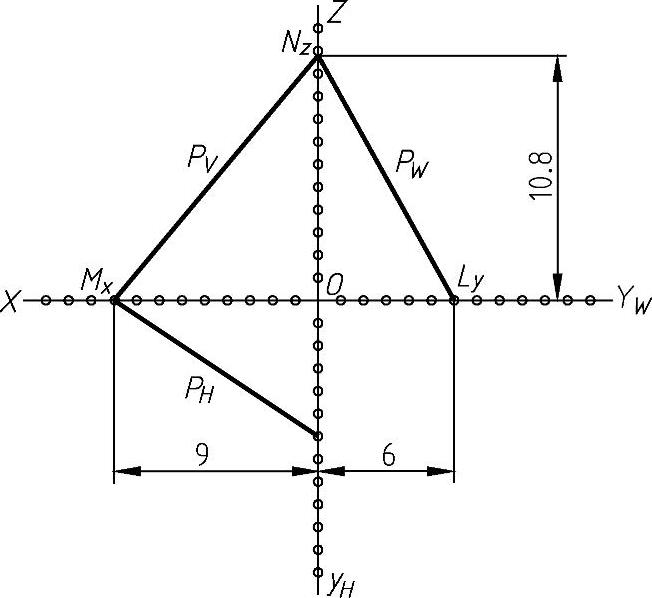
图1-14 由平面方程转换成投影图
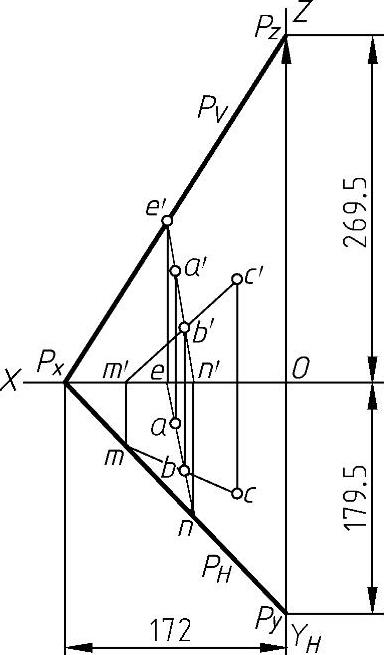
图1-15 由平面投影图 转换成方程
解 将A、B、C三点所代表的平面转换成迹线平面。具体步骤为:连接A、B两点为AB直线,延长AB直线并求出其与H投影面的交点N。同样,连接B、C两点为BC直线,延长BC直线并求出其与H投影面的交点M。N、M称为水平迹点,将此两个水平迹点用直线相连,得到A、B、C三点所代表的平面的水平迹线PH,延长PH与X轴交于Px点,平面的正面迹线PV必过Px点,因此只需再求出一个正面面迹点E,将E点与Px点用直线相连就得到了正面迹线PV。为此,将A、B两点连接成AB直线,延长AB直线求出其与V面的交点即为E点,如图1-15所示。将A、B、C三点所代表的平面转换成迹线平面后,量取三个坐标轴的截距为:a=172,b=179.5,c=269.5,由此得到平面的截距式方程为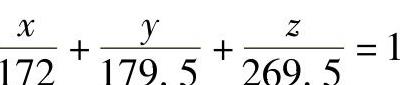 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




