【摘要】:斯托克斯公式是格林公式的推广,格林公式建立了平面区域上的二重积分与其边界曲线上的曲线积分之间的联系,而斯托克斯公式则建立了沿曲面Σ的曲面积分与沿Σ的边界曲线L的曲线积分之间的联系.在引入斯托克斯公式之前,先对有向曲面Σ的侧与其边界曲线L的方向作以下规定:右手法则设Σ是空间上的光滑曲面,其边界曲线为L,取定Σ的一侧为正侧,伸开右手手掌,以拇指方向指向此侧的法线正向,其余四指伸开微曲,并使曲面Σ在手
斯托克斯公式是格林公式的推广,格林公式建立了平面区域上的二重积分与其边界曲线上的曲线积分之间的联系,而斯托克斯公式则建立了沿曲面Σ的曲面积分与沿Σ的边界曲线L的曲线积分之间的联系.
在引入斯托克斯公式之前,先对有向曲面Σ的侧与其边界曲线L的方向作以下规定:
右手法则 设Σ是空间上的光滑曲面,其边界曲线为L,取定Σ的一侧为正侧,伸开右手手掌,以拇指方向指向此侧的法线正向,其余四指伸开微曲,并使曲面Σ在手掌的左侧,则其余四指所指的方向就是边界曲线L的正方向,反之亦然(见图11-38).
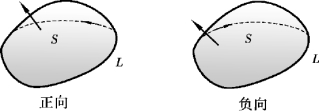
图11-38
定理2 设L为分段光滑的空间有向闭曲线,Σ是以L为边界的分片光滑的有向曲面,L的正向与Σ的侧符合右手规则,函数P(x,y,z),Q(x,y,z),R(x,y,z)在曲面Σ(连同边界)上具有一阶连续偏导数,则有
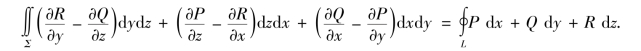
记忆方式为
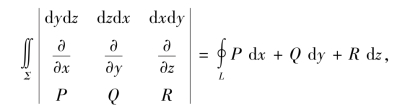
或
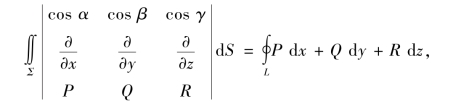
图11-39(https://www.xing528.com)
其中,n=(cosα,cosβ,cosγ)为有向曲面Σ在点(x,y,z)处的单位法向量.

解 设Σ为闭曲线L所围成的三角形平面,Σ在yOz面、zOx面和xOy面上的投影区域分别为Dyz,Dzx和Dxy.根据斯托克斯公式,有

例5 利用斯托克斯公式计算曲线积分
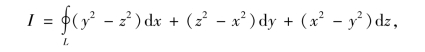

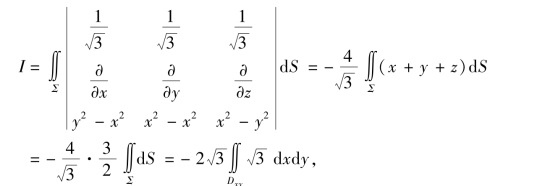
其中,Dxy为Σ在xOy平面上的投影区域(见图11-40(b)),于是
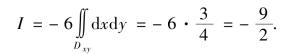
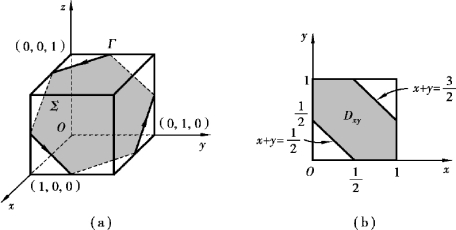
图11-40
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




