【摘要】：给定一向量场其中，函数P（x，y，z），Q（x，y，z），R（x，y，z）具有一阶连续偏导数，则称为向量场A在点（x0，y0，z0）处的散度，记作divA（x0，y0，z0）.一般地，就表示A在场中任一点（x，y，z）处的散度.第二类曲面积分称为向量场A通过曲面Σ流向指定侧的通量.通量的向量形式是其中，n是曲面Σ在点（x，y，z）处的单位法向量.对向量场A，若将这里的Σ看成高斯公式中区域Ω的边界（
给定一向量场
其中，函数P（x，y，z），Q（x，y，z），R（x，y，z）具有一阶连续偏导数，则
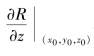称为向量场A在点（x0，y0，z0）处的散度，记作divA（x0，y0，z0）.
一般地，
就表示A在场中任一点（x，y，z）处的散度.
第二类曲面积分
称为向量场A通过曲面Σ流向指定侧的通量.
通量的向量形式是
其中，n是曲面Σ在点（x，y，z）处的单位法向量.
对向量场A，若将这里的Σ看成高斯公式中区域Ω的边界（闭）曲面，且按高斯公式，Σ取外侧，则有
右端表示在单位时间内离开区域Ω的流量.假设流体是稳定流动且不可压缩的，因此，在流体离开区域Ω的同时，在Ω内部就应该由流体的“源头”产生出同样多的流体来补充，所以高斯公式的左端可解释为分布在Ω内的源头在单位时间内所产生的流量.(www.xing528.com)
例3 求向量场r=xi+yj+zk的通量，其中曲面分别为：
（1）穿过圆锥x2+y2≤z2（0≤z≤h）的底（向上）.
（2）穿过圆锥x2+y2≤z2（0≤z≤h）的侧表面（向外）.
解 设Σ1，Σ2及Σ分别为此圆锥的底面、侧面及全表面，则穿过全表面向外的通量为
（1）穿过底面向上的通量为
（2）穿过侧表面向外的通量为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
