第一型曲面积分的概念及性质简介

在引入第一型曲面积分的概念之前，首先要介绍光滑曲面的概念.所谓光滑曲面，是指曲面上每一点都有切平面，且切平面的法向量随着曲面上的点连续变动而连续变化.所谓的分片光滑曲面，是指曲面是由有限个光滑曲面逐片拼起来的.例如，椭球面是光滑曲面，立方体的边界面是分片光滑曲面.本节讨论的曲面都是指光滑曲面或分片光滑曲面.

类似于第一型曲线积分，面密度函数ρ（x，y，z）在曲面Σ上连续时，曲面Σ的质量为

图11-26

其中，λ为各小块曲面直径的最大值.

抽去具体的物理意义，就得到第一型曲面积分的概念.

定义1　设曲面Σ是光滑的，函数f（x，y）在Σ上有界.把Σ任意分成n小块ΔS1，ΔS2，…，ΔSn（ΔSi同时代表第i个小块曲面的面积），在ΔSi上任取一点（ξi，ηi，ζi）（见图11-26），如果当各小块曲面的直径的最大值λ→0时，极限ΔSi总存在，则称此极限为函数f（x，y，z）在曲面Σ上的第一型曲面积分或对面积的曲面积分，记作，即(www.xing528.com)

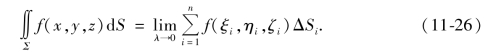
其中，f（x，y，z）称为被积函数，Σ称为积分曲面.

当f（x，y，z）在光滑曲面Σ上连续时第一型曲面积分总是存在的.今后总假定f（x，y，z）在Σ上连续.

特别地，当f（x，y，z）≡1时，有

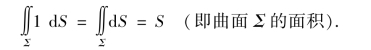
根据上述定义，光滑曲面Σ的面密度为ρ（x，y，z），则曲面Σ的质量M可表示为ρ（x，y，z）在Σ上的第一型曲面积分