第二型曲线积分的计算结果

定理1　设P（x，y），Q（x，y）是定义在光滑有向曲线

上的连续函数，当参数t单调地由α变到β时，点M（x，y）从L的起点A沿L方向运动到终点B则

对沿封闭曲线L的第二型曲线积分的计算，可在L上任意选取一点作为起点，沿L所指定的方向前进，最后回到这一点.

若空间曲线L的参数方程为

则

其中，α对应于L的起点，β对应于L的终点.

解　L的参数方程为x=t，y=t，t从0变到1，则

图11-15

方法2：以y为参数.L的方程为x=y2，y从-1变到1.因此

例3　计算∫L2xy dx+x2dy，其中L为：

（1）抛物线y=x2上从O（0，0）到B（1，1）的一段弧；

（2）抛物线x=y2上从O（0，0）到B（1，1）的一段弧；(https://www.xing528.com)

（3）有向折线OAB，这里O，A，B依次是点（0，0），（1，0），（1，1）.

解　（1）化为对x的定积分.L：y=x2，x从0变到1.因此

（2）化为对y的定积分.L：x=y2，y从0变到1.因此

在OA上，y=0，x从0变到1.因此

在AB上，x=1，y从0变到1.因此

从而

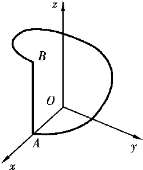
图11-16

由例3可知，虽然沿不同路径，曲线积分的值可以相等.

例4　求质点在力场F=（y，-x，z）作用下由A（R，0，0）沿L移动到B（R，0，2kπ）（见图11-16）所做的功，其中L为

（1）x=R cos t，y=R sin t，z=kt，0≤t≤2π;

（2）直线AB.

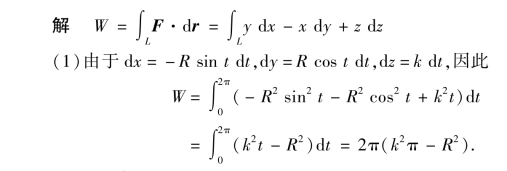
（2）L的参数方程为x=R，y=0，z=t，t从0变到2kπ.

由于dx=0，dy=0，dz=dt.因此