微积分（下册）：第一型曲线积分的概念与性质

首先讨论曲线形构件的质量问题.

一般来说，根据实际问题的需要，曲线形构件各部分的粗细程度不完全一样，故线密度（即单位长度的质量）是变化的.

图11-10

设构件为xOy平面内一条有质量的曲线L（见图11-10），L上任一点（x，y）处的线密度为ρ（x，y），试求该构件的质量m.

如果构件的线密度是常量ρ，则其质量就等于它的线密度ρ与长度的乘积.如果线密度是变量，就不能直接用上述方式来计算.可采用类似于定积分和重积分的方法，即将曲线L任意分成n个弧段Li，分点为Mi（i=0，1，2，…，n），各弧段及其弧长都记作Δsi（i=1，2，…，n），如图11-10所示.设mi为弧段Δsi的质量，当分割充分细密时，每个弧段上的密度ρ（x，y）可看成均匀的，任取（ξi，ηi）∈Li，得第i小段质量的近似值为

将各弧段上的质量相加，可得质量m的近似值

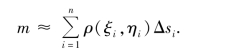
当L分割得到越来越细（即λ=max{Δs1，Δs2，…，Δsn}→0），则可得整个曲线构件的质量为

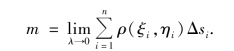
这种和的极限在研究其他问题时也会遇到，因此，给出以下概念：

其中，f（x，y）称为被积函数，L称为积分弧段，ds称为弧长微元.

根据定义，若f（x，y）≡1，则有(www.xing528.com)

特别地，如果L是闭曲线，那么函数f（x，y）在闭曲线L上的第一型曲线积分记作

若L为空间上的光滑曲线段，f（x，y，z）为定义在L上的函数，则可类似地定义f（x，y，z）在空间曲线L上的第一型曲线积分，记作

　这样，本节开始所求的曲线形构件的质量可表示为

第一型曲线积分也和定积分一样具有下述重要性质.

性质1（线性性）　设α，β为任意常数，则

性质2（路径可加性）　若积分弧段L可分成两段光滑曲线弧L1和L2，则