【摘要】：图11-7易知，点M的直角坐标（x，y，z）与球面坐标（r，φ，θ）之间的关系为球面坐标系中的三簇坐标面分别为：r=常数，即以原点（0，0，0）为球心的球面；φ=常数，即以原点为顶点、z轴为对称轴的圆锥面；θ=常数，即一簇过z轴的半平面.图11-8现在来考察三重积分在球面坐标系下的形式.为此，用球面坐标系中的三簇坐标面把空间区域Ω划分成许多小闭区域.考虑由r，φ，θ分别取得的微小增量dr，dφ，d
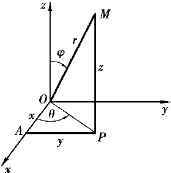
图11-7
易知，点M的直角坐标（x，y，z）与球面坐标（r，φ，θ）之间的关系为
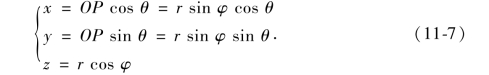
球面坐标系中的三簇坐标面分别为：
r=常数，即以原点（0，0，0）为球心的球面；
φ=常数，即以原点为顶点、z轴为对称轴的圆锥面；
θ=常数，即一簇过z轴的半平面.
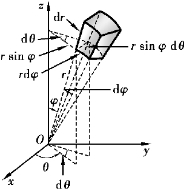
图11-8
现在来考察三重积分在球面坐标系下的形式.为此，用球面坐标系中的三簇坐标面把空间区域Ω划分成许多小闭区域.考虑由r，φ，θ分别取得的微小增量dr，dφ，dθ所成的“六面体”的体积dv，如图11-8所示.
在不计高阶无穷小时，这个体积可近似地看成长方体，3边长分别为r dφ，r sinφdθ，dr，于是得
这就是球面坐标的体积元素.再用关系式（11-7），就得到球面坐标系下三重积分的表达式
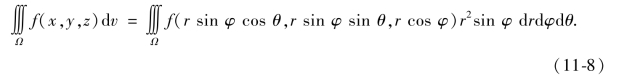(www.xing528.com)
注 当被积函数含有x2+y2+z2，积分区域是球面围成的区域或由球面及锥面围成的区域等，并且在球面坐标变换下，区域用r，φ，θ表示较简单时，利用球面坐标变换能简化积分的计算.
特别地，当积分区域Ω为球面r=a所围成时，则有
如果f（r sinφcosθ，r sinφsinθ，r cosφ）=1，由上式即得球的体积为
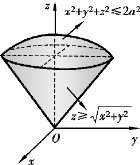
图11-9
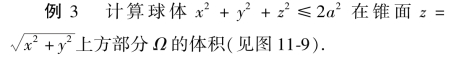
解 由三重积分的性质可知
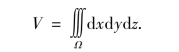
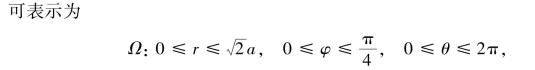
所以
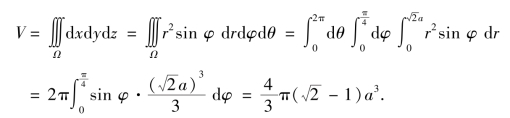
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
